当前位置:网站首页>Cartoon: looking for the k-th element of an unordered array (Revised)
Cartoon: looking for the k-th element of an unordered array (Revised)
2022-07-05 17:28:00 【Small ash】
This article modifies two details :
1. Method 2 , Insert the array A The condition is to traverse to the element “ Greater than ” Array A The smallest element of , Instead of ” Less than ”.
2. Method 3 , node 24 When the little top pile sinks , It should be connected to nodes 17 In exchange for , Not with nodes 20 In exchange for .
Thank you for your correction .
————— the second day —————
What does the title mean ? For example, given an unordered array as follows :
If k=6, That is to look for the second 6 Big elements , Which element is this ?
obviously , The largest element in the array is 24, The second largest element is 20, The third element is 17 ...... The first 6 The big element is 9.
Method 1 : Sequencing
This is the easiest way to think of , First, sort the unordered array from large to small , After the order k Elements , Nature is the number one in the array k Big element .
Method 2 : Insertion method
Maintain a length of k Array of A Ordered array of , Used to store known k A larger element .
Next, traverse the original array , Every time you traverse to an element , And an array A Compared with the smallest element in , If it is less than or equal to the array A The smallest element of , Continue traversing ; If it's larger than the array A The smallest element of , Then insert it into the array A in , And put the smallest element ever “ Squeeze out ”.
such as k=3, Let's start with the leftmost 7,5,15 Put three numbers in an array in order A among , Represents the current three largest numbers .
Now , Traversing 3, because 3<5, Continue traversing .
Next we go through to 17, because 17>5, Insert into array A The right place , Similar to insert sort , And put the smallest element 5“ Squeeze out ”.
Continue traversing the original array , All the way to the last element of the array ......
Final , Array A The elements stored in are 24,20,17, Represents the largest... In the entire array 3 Elements . Now the array A The smallest element in 17 That's what we're looking for k Big element .
————————————
What is a binary heap ? If you don't know much about it, you can read this article first : comic : What is a binary heap ?( Revised version )
In short , A binary heap is a special kind of complete binary tree , It consists of two forms: large top pile and small top pile .
Among them, the characteristics of small top reactor , Every parent node is less than or equal to its own child node . To solve this algorithmic problem , We can use Small cap pile Characteristics of .
Method 3 : Small top pile method
Maintain a capacity of k The little top pile , Heap k Nodes represent The biggest... At present k Elements , And the top of the pile is obviously this k Of the elements minimum value .
Iterate over the original array , One element per iteration , Compared to the top of the heap , If the current element is less than or equal to the top of the heap , Then continue to traverse ; If the element is larger than the top of the heap , Put the current element at the top of the heap , And adjust the fork stack ( Sinking operation ).
After the traversal is over , The top of the heap is an array Maximum k The minimum of the elements , That is to say The first k Big element .
hypothesis k=5, The specific implementation steps are as follows :
1. Put the front of the array k Elements are built into a heap .
2. Continue traversing the array , Compared to the top of the heap , If it is less than or equal to the top of the heap , Then continue to traverse ; If it's larger than the top of the pile , Replace the top element and adjust the heap .
Traverse to element 2, because 2<3, So continue traversing .
Traverse to element 20, because 20>3,20 Instead of the top position , And adjust the pile .
Traverse to element 24, because 24>5,24 Instead of the top position , And adjust the pile .
And so on , We traverse the elements one by one , When traversing to the last element 8 When , The situation of small top reactor is as follows :
3. The top of the heap at this time , It's the minimum in the heap , That is, the first in the array k Big element .
What is the time complexity of this method ?
1. The time complexity of building a heap is O(k)
2. The time complexity of traversing the remaining array is O(n-k)
3. The time complexity of each heap adjustment is O(logk)
among 2 and 3 It's a nested relationship ,1 and 2,3 It's juxtaposition , So the total worst-case time complexity is O((n-k)logk + k). When k Far less than n Under the circumstances , It can also be approximately regarded as O(nlogk).
What is the spatial complexity of this method ?
Just now, we showed the binary heap separately in the detailed steps , To make it easy to understand . But if it's allowed to change the original array , We can put the front of the array k Elements “ In situ exchange ” To build a binary reactor , This eliminates the need to open up additional storage space .
therefore , The spatial complexity of the method is O(1).
/**
* Search for the first k Big elements
* @param array The heap to be adjusted
* @param k What is the largest
*/
public static int findNumberK(int[] array, int k){
//1. Before use k Elements to build a small top heap
buildHeap(array, k);
//2. Continue traversing the array , Compared to the top of the heap
for(int i=k; i<array.length;i++){
if(array[i] > array[0]){
array[0] = array[i];
downAdjust(array, 0, k);
}
}
//3. Return to the top of heap element
return array[0];
}
/**
* Build heap
* @param array The heap to be adjusted
* @param length The effective size of the heap
*/
private static void buildHeap(int[] array, int length) {
// Start with the last non leaf node , Adjust in turn
for (int i = (length-2)/2; i >= 0; i--) {
downAdjust(array, i, length);
}
}
/**
* Sinking adjustment
* @param array The heap to be adjusted
* @param index The node to sink
* @param length The effective size of the heap
*/
private static void downAdjust(int[] array, int index, int length) {
// temp Save the parent node value , For the final assignment
int temp = array[index];
int childIndex = 2 * index + 1;
while (childIndex < length) {
// If there is a right child , And the right child is less than the left child , Then locate the right child
if (childIndex + 1 < length && array[childIndex + 1] < array[childIndex]) {
childIndex++;
}
// If the parent node is less than the value of any child , Direct jump out
if (temp <= array[childIndex])
break;
// There's no real exchange , One way assignment is enough
array[index] = array[childIndex];
index = childIndex;
childIndex = 2 * childIndex + 1;
}
array[index] = temp;
}
public static void main(String[] args) {
int[] array = new int[] {7,5,15,3,17,2,20,24,1,9,12,8};
System.out.println(findNumberK(array, 5));
}Method four : Divide and conquer method
We all know about quick sort , Quicksort uses divide and conquer , Divide the array into larger and smaller parts each time .
We're looking for number one k When it comes to big elements , You can also use this idea , With a certain element A Benchmarking , Make greater than A Are swapped to the left of the array , Less than A All of the elements are swapped to the right of the array .
For example, we choose elements 7 As a benchmark , Divide the array into larger ones on the left , Two smaller areas on the right , The exchange results are as follows :
Including elements 7 The larger elements inside are 8 individual , But our k=5, Obviously there are too many larger elements . So we continue to divide and conquer the larger element regions , This time with elements 12 Bit reference :
thus , Including elements 12 The larger elements inside are 5 individual , Coincides with k equal . therefore , Reference elements 12 That's what we're looking for .
This is the general idea of divide and conquer , The time complexity of this method is even better than that of the small top pile method , You can achieve O(n). Interested partners can try to use the code to achieve it .
Found this article useful , Please give it a good look , I think it's very useful , Please forward it to your friends .
边栏推荐
- 独立开发,不失为程序员的一条出路
- Check the WiFi password connected to your computer
- Force deduction solution summary 729- my schedule I
- Kafaka technology lesson 1
- Rider 设置选中单词侧边高亮,去除警告建议高亮
- Precision epidemic prevention has a "sharp weapon" | smart core helps digital sentinels escort the resumption of the city
- Embedded-c Language-5
- easyNmon使用汇总
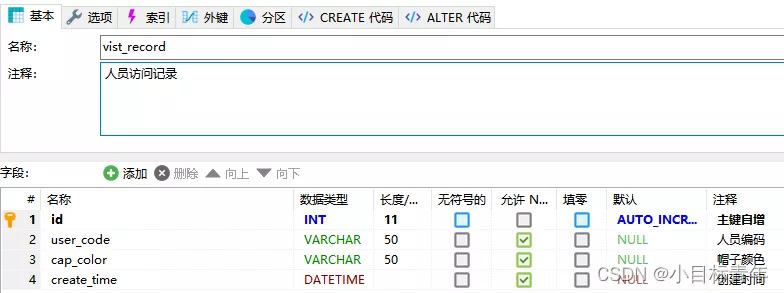
- 33: Chapter 3: develop pass service: 16: use redis to cache user information; (to reduce the pressure on the database)
- Embedded-c Language-3
猜你喜欢
Embedded UC (UNIX System Advanced Programming) -2

Embedded UC (UNIX System Advanced Programming) -1
Judge whether a number is a prime number (prime number)
MySql 查询符合条件的最新数据行

机器学习01:绪论
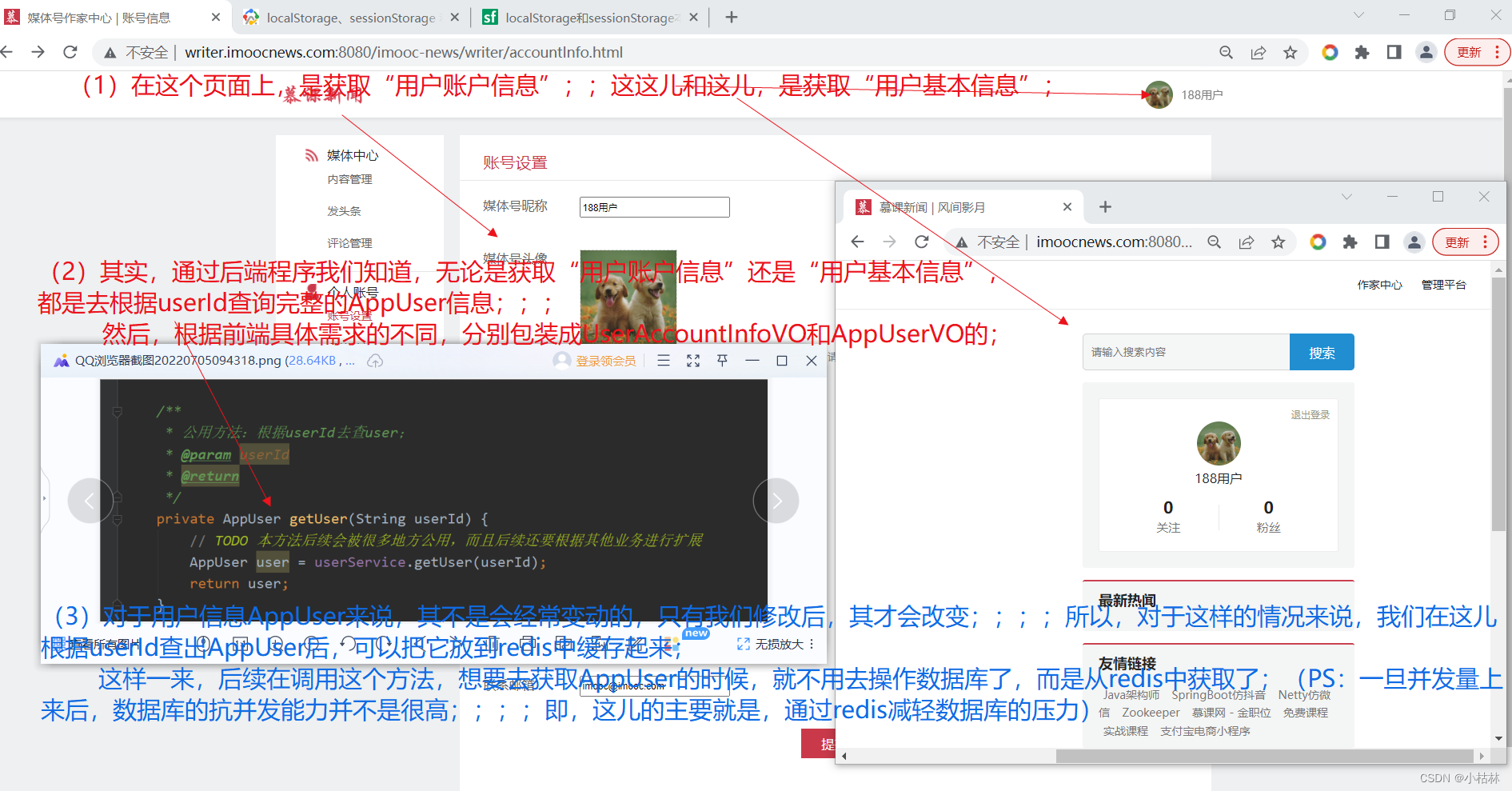
33:第三章:开发通行证服务:16:使用Redis缓存用户信息;(以减轻数据库的压力)
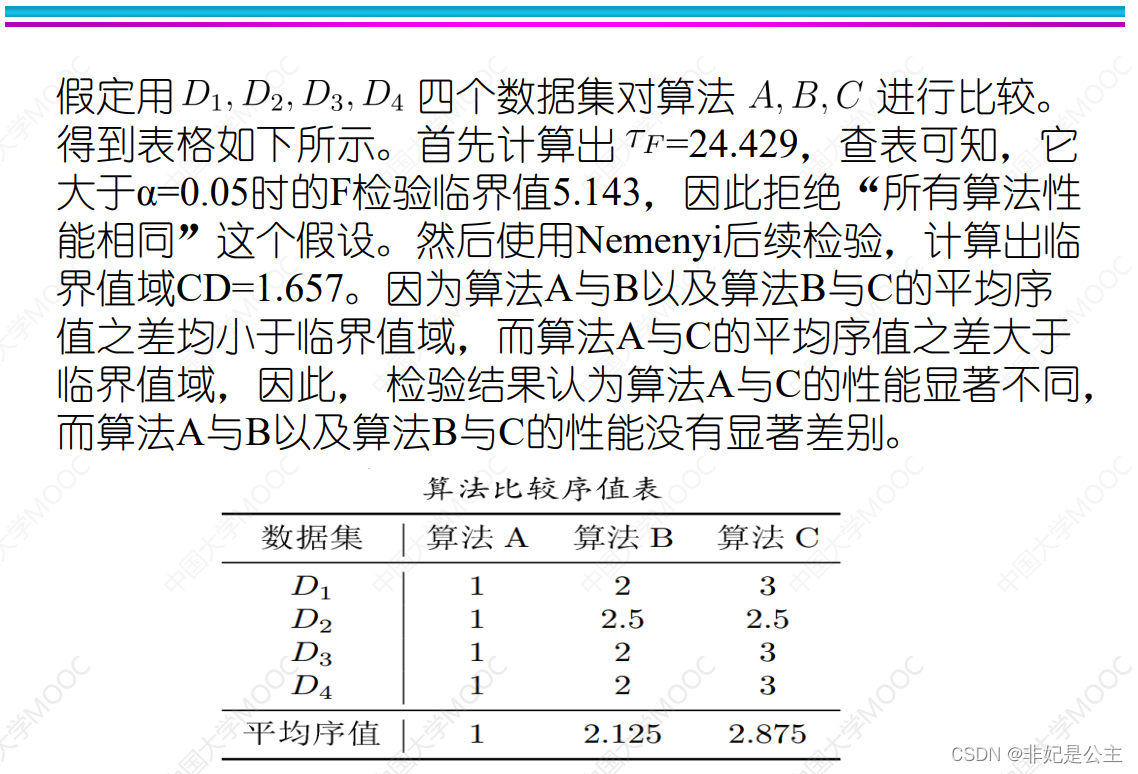
机器学习02:模型评估

Machine learning 01: Introduction

Which is more cost-effective, haqu K1 or haqu H1? Who is more worth starting with?
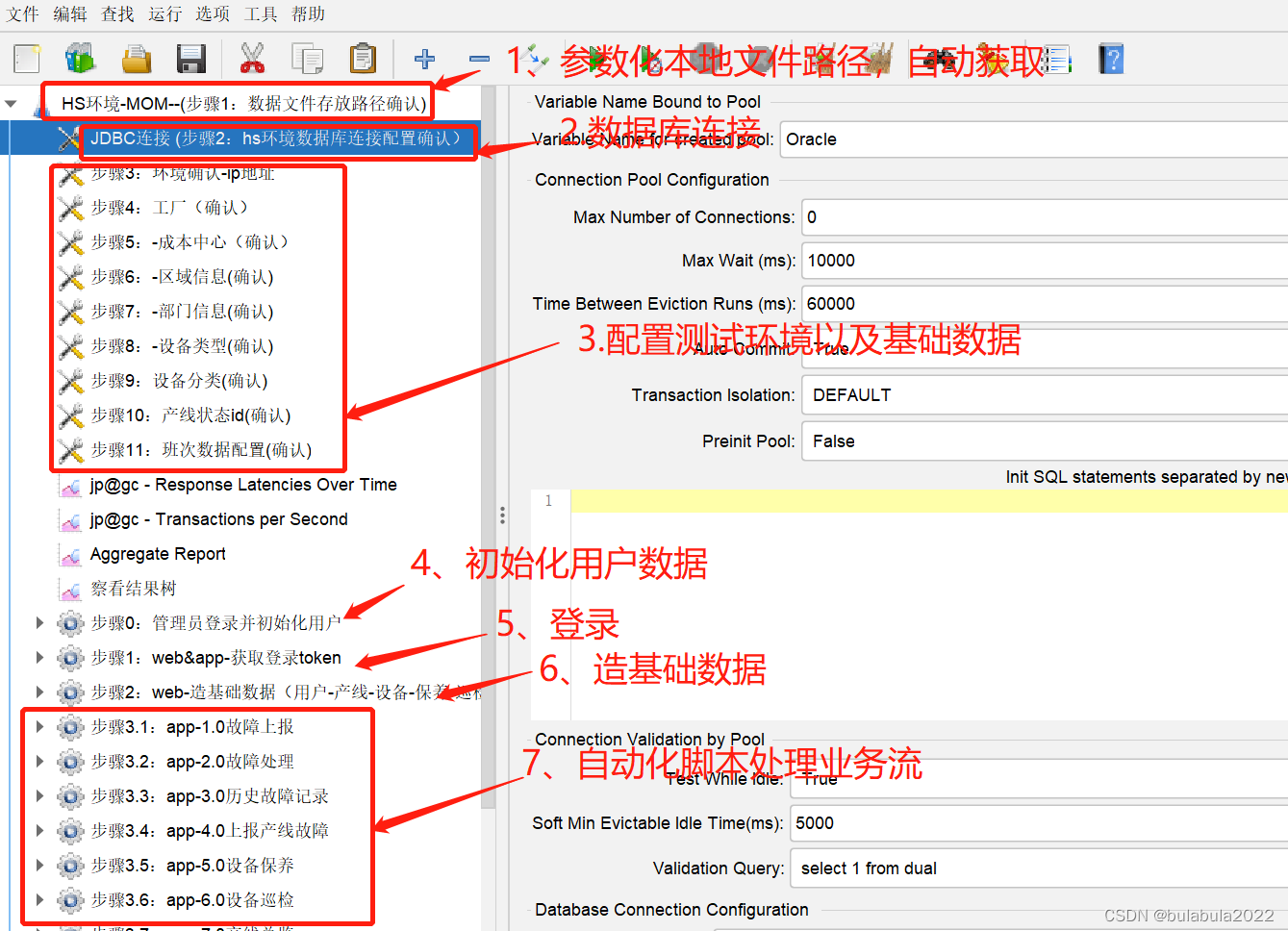
【jmeter】jmeter脚本高级写法:接口自动化脚本内全部为变量,参数(参数可jenkins配置),函数等实现完整业务流测试
随机推荐
【beanshell】数据写入本地多种方法
Read the basic grammar of C language in one article
漫画:如何实现大整数相乘?(整合版)
这个17岁的黑客天才,破解了第一代iPhone!
Three traversal methods of binary tree
mysql中取出json字段的小技巧
First day of learning C language
Zhang Ping'an: accelerate cloud digital innovation and jointly build an industrial smart ecosystem
CVPR 2022 best student paper: single image estimation object pose estimation in 3D space
关于mysql中的json解析函数JSON_EXTRACT
Flow characteristics of kitchen knife, ant sword, ice scorpion and Godzilla
Oracle缩表空间的完整解决实例
Domain name resolution, reverse domain name resolution nbtstat
机器学习02:模型评估
查看自己电脑连接过的WiFi密码
Embedded-c Language-3
[binary tree] insufficient nodes on the root to leaf path
Is it safe to open futures accounts online? Will there be more liars online? Doesn't feel very reliable?
flask解决CORS ERR 问题
Learn about MySQL transaction isolation level