当前位置：网站首页>[set theory] relational closure (relational closure solution | relational graph closure | relational matrix closure | closure operation and relational properties | closure compound operation)

[set theory] relational closure (relational closure solution | relational graph closure | relational matrix closure | closure operation and relational properties | closure compound operation)

2022-07-03 06:11:00 【Programmer community】

List of articles

One 、 Closure method
Two 、 Find an example of closure ( Diagram angle )
3、 ... and 、 Find an example of closure ( Relationship matrix angle )
Four 、 Closure operation and relation properties
5、 ... and 、 Closure compound operation

One 、 Closure method

$R$ The relationship is

$A$ Binary relations on sets ,

⊆

R \subseteq A

$R \subseteq A$ , And

$A$ Set is not empty ,

≠

∅

A \not= \varnothing

$A \neq = \emptyset$

Find reflexive closure :

(

)

∪

r(R) = R \cup I_A

$r (R) = R \cup I_{A}$ , Add a ring to each vertex ;

If $I_A \subseteq R$
$I_{A} \subseteq R$

Find symmetric closure :

(

)

∪

−

s(R) = R \cup R^{-1}

$s (R) = R \cup R^{- 1}$

original There is no edge ( Ordered pair ) , Naturally, there is no corresponding inverse , Do not add edges at this time
original There is a directed side ( Ordered pair ) , Add a reverse directed edge , form In the diagram Between vertices Two way directed edge
original There are two directed edges ( Ordered pair ) , At this time, there is no need to add other edges
If $R^{-1}$
$R = R^{- 1}$

Finding transitive closure :

(

)

∪

⋯

t(R) = R \cup R^2 \cup R^3 \cup \cdots

$t (R) = R \cup R^{2} \cup R^{3} \cup \dots$

take

$R$ Relate all the power operation values together , Is its transitive closure ,

$R$ Relational

$1$ The next power ,

$R$ Relational

$2$ The next power ,

$R$ Relational

$3$ The next power ,

⋯

\cdots

$\dots$ ,

$R$ Relational

$n$ The next power , And get up , Is its transitive closure ;

$A$ It's a poor set , The relationship is also poor , Find out all

$n$ The next power , There is no need to find many power operations , Because the power operation of the relationship is followed by a cycle , Find all known

$n$ The next power take Union is enough ;

$R$ Relationships are transitive , If and only if ,

⊆

R^2 \subseteq R

$R^{2} \subseteq R$

Two 、 Find an example of closure ( Diagram angle )

aggregate

{

}

A = \{ a, b, c , d \}

$A = {a, b, c, d}$

Relationship

{

}

R = \{ <a,b> , <b,a> , <b,c> , <c,d> \}

$R = {< a, b >, < b, a >, < b, c >, < c, d >}$

Seeking relationship

$R$ Reflexive closure of

(

)

r(R)

$r (R)$ , Symmetric closure

(

)

s(R)

$s (R)$ , Pass closures

(

)

t(R)

$t (R)$

Insert picture description here

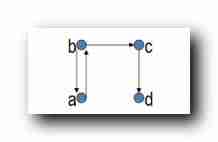
Find reflexive closure : Is to add a ring to each vertex :

Insert picture description here

Find symmetric closure : take Between vertices Change one-way edge to two-way edge , No matter Two way edges between vertices and There are no edges between vertices The situation of ;

Insert picture description here

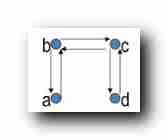
Finding transitive closure : Connect the accessible points directly ;

a You can go to b , route a -> b ; a You can go to c , The path is a a -> b -> c ; a You can go to d , The path is a a -> b -> c -> d ; So add a To c , d The directed side of ;
b You can go to a , route b -> a ; b You can go to c , The path is a b -> c ; b You can go to d , The path is a b -> c -> d ; So add b To d The directed side of ;
c You can go to d , route c -> d ; There are no connectable edges ;
d I can't get anywhere , There are no connectable edges ;
In addition, when two-way edges appear , Two vertices must be looped ;

Insert picture description here

3、 ... and 、 Find an example of closure ( Relationship matrix angle )

Relationship

{

}

R = \{ <a, b> , <b,a> , <b,c> , <c,d> \}

$R = {< a, b >, < b, a >, < b, c >, < c, d >}$

Use the relation matrix method to find its Reflexive closure , Symmetric closure , Pass closures ;

Write the above relationship in matrix form as :

(

)

[

]

M(R) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}

$M (R) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001000010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

Reflexive closure : Set the main diagonal value , All changed

$1$ , The upper left corner to the lower right corner is the main diagonal ;

(

)

[

]

M(r(R)) = \begin{bmatrix} 1 & 1 & 0 & 0 \\\\ 1 & 1 & 1 & 0 \\\\ 0 & 0 & 1 & 1 \\\\ 0 & 0 & 0 & 1 \end{bmatrix}

$M (r (R)) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1100110001100011 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

Symmetric closure : Both ends of the main diagonal should be symmetrical , Based on the diagonal , Make the values on both sides of the diagonal symmetrical ;

(

)

[

]

M(s(R)) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 1 & 0 \end{bmatrix}

$M (s (R)) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100101001010010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

Pass closures : Find the of the relation matrix second power , third power , fourth power ,

⋯

\cdots

$\dots$ , Until the value of the same cycle appears ;

Put all the above different Matrix power operation Add logically ( or ) operation , Is the matrix corresponding to its transitive closure , Computer algorithm is suitable for this method , If people calculate , The diagram is more vivid ;

Pay attention to reverse order synthesis

(

)

(

∘

)

(

)

∙

(

)

[

]

∙

[

]

[

]

M(R^2) = M(R \circ R) = M(R) \bullet M(R) =\begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}

$M (R^{2}) = M (R \circ R) = M (R) ∙ M (R) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001000010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∙ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001000010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1000010010000100 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

(

)

(

∘

)

(

)

∙

(

)

[

]

∙

[

]

[

]

M(R^3) = M(R^2 \circ R) = M(R) \bullet M(R^2) = \begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 1 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}

$M (R^{3}) = M (R^{2} \circ R) = M (R) ∙ M (R^{2}) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001000010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∙ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1000010010000100 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001001000 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

(

)

(

∘

)

(

)

∙

(

)

[

]

∙

[

]

[

]

(

)

M(R^4) = M(R^3 \circ R) = M(R) \bullet M(R^3) =\begin{bmatrix} 0 & 1 & 0 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} \bullet \begin{bmatrix} 0 & 1 & 0 & 1 \\\\ 1 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 0 \\\\ 0 & 1 & 0 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix} = M(R^2)

$M (R^{4}) = M (R^{3} \circ R) = M (R) ∙ M (R^{3}) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001000010 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ∙ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0100100001001000 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1000010010000100 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = M (R^{2})$

Therefore, its

R^4

$R^{4}$ The subsequent power operation value , Even power relation matrix and

(

)

M(R^2)

$M (R^{2})$ Same value , Odd power relation matrix and

(

)

M(R^3)

$M (R^{3})$ Same value ;

(

)

(

)

∨

(

)

∨

(

)

[

]

M(t(R)) = M(R) \lor M(R^2) \lor M(R^3) =\begin{bmatrix} 1 & 1 & 1 & 1 \\\\ 1 & 1 & 1 & 1 \\\\ 0 & 0 & 0 & 0 \\\\ 0 & 0 & 0 & 0 \end{bmatrix}

$M (t (R)) = M (R) \lor M (R^{2}) \lor M (R^{3}) = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 1100110011001100 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤$

Four 、 Closure operation and relation properties

	reflexivity	symmetry	Transitivity

The median value in the above table is

$1$ , It shows that this property originally exists , Find the corresponding introspect / symmetry / Pass on After closure , It still has this property , On the contrary, it does not have this property ;

The meaning of the second row of the table :

(

)

r(R)

$r (R)$ The corresponding line ;

reflexivity : If
symmetry : If
Transitivity : If

There is only one exception : original

$R$ It's delivered , If we find symmetric closures , The transitivity of its symmetric closure does not exist ;

Description of the second column of the table ( reflexivity ) : If

$R$ Relationships are reflexive , So Symmetric closure

(

)

s(R)

$s (R)$ and Pass closures

(

)

t(R)

$t (R)$ It's also reflexive ;

since

back

⇒

(

)

and

(

)

since

back

R introspect \Rightarrow s(R) and t(R) introspect

$R since back \Rightarrow s (R) and t (R) since back$

The third column of the table explains ( symmetry ) : If

$R$ The relationship is symmetrical , So Reflexive closure

(

)

r(R)

$r (R)$ and Pass closures

(

)

t(R)

$t (R)$ It's also symmetrical ;

Yes

call

⇒

(

)

and

(

)

Yes

call

R symmetry \Rightarrow r(R) and t(R) symmetry

$R Yes call \Rightarrow r (R) and t (R) Yes call$

The fourth column of the table explains ( Transitivity ) : If

$R$ Relationships are transitive , So Reflexive closure

(

)

r(R)

$r (R)$ It is also transmitted ;

Pass on

Deliver

⇒

(

)

Pass on

Deliver

R Pass on \Rightarrow r(R) Pass on

$R Pass on Deliver \Rightarrow r (R) Pass on Deliver$

5、 ... and 、 Closure compound operation

$R$ The relationship is

$A$ Binary relations on sets ,

⊆

R \subseteq A

$R \subseteq A$ , And

$A$ Set is not empty ,

≠

∅

A \not= \varnothing

$A \neq = \emptyset$

(

)

(

)

rs(R) = sr(R)

$r s (R) = s r (R)$ :

rs( R ) : First seek
sr( R ) : First seek
The above two closure operations The result is the same

(

)

(

)

rt(R) = tr(R)

$r t (R) = t r (R)$

rt( R ) : First seek
tr( R ) : First seek
The above two closure operations The result is the same

(

)

⊆

(

)

st(R) \subseteq ts(R)

$s t (R) \subseteq t s (R)$

st( R ) : First seek
ts( R ) : First seek
The results of the above two closure operations ,
$s t (R)$ Relationship ;

原网站

版权声明
本文为[Programmer community]所创，转载请带上原文链接，感谢
https://yzsam.com/2022/02/202202150616325283.html

当前位置：网站首页>[set theory] relational closure (relational closure solution | relational graph closure | relational matrix closure | closure operation and relational properties | closure compound operation)

[set theory] relational closure (relational closure solution | relational graph closure | relational matrix closure | closure operation and relational properties | closure compound operation)

List of articles

One 、 Closure method

Two 、 Find an example of closure ( Diagram angle )

3、 ... and 、 Find an example of closure ( Relationship matrix angle )

Four 、 Closure operation and relation properties

5、 ... and 、 Closure compound operation

边栏推荐

猜你喜欢

随机推荐