第六章-6.1-堆-6.2-维护堆的性质-6.3-建堆

6.1 堆

1、概念：

如图1所示，（二叉）堆是一个数组，它可以被看成一个近似完全的二叉树（除了其底层外这个树是填满的且从左向右填充的）。

2、属性

（1）A.length:通常给出数组元素个数

（2）A.heap-size:多少个堆元素存储在该数组中。

二者区别在于A[1…A.length]中可能都存有数据，但是只有A[1…A.heap-size]中的元素是有效的。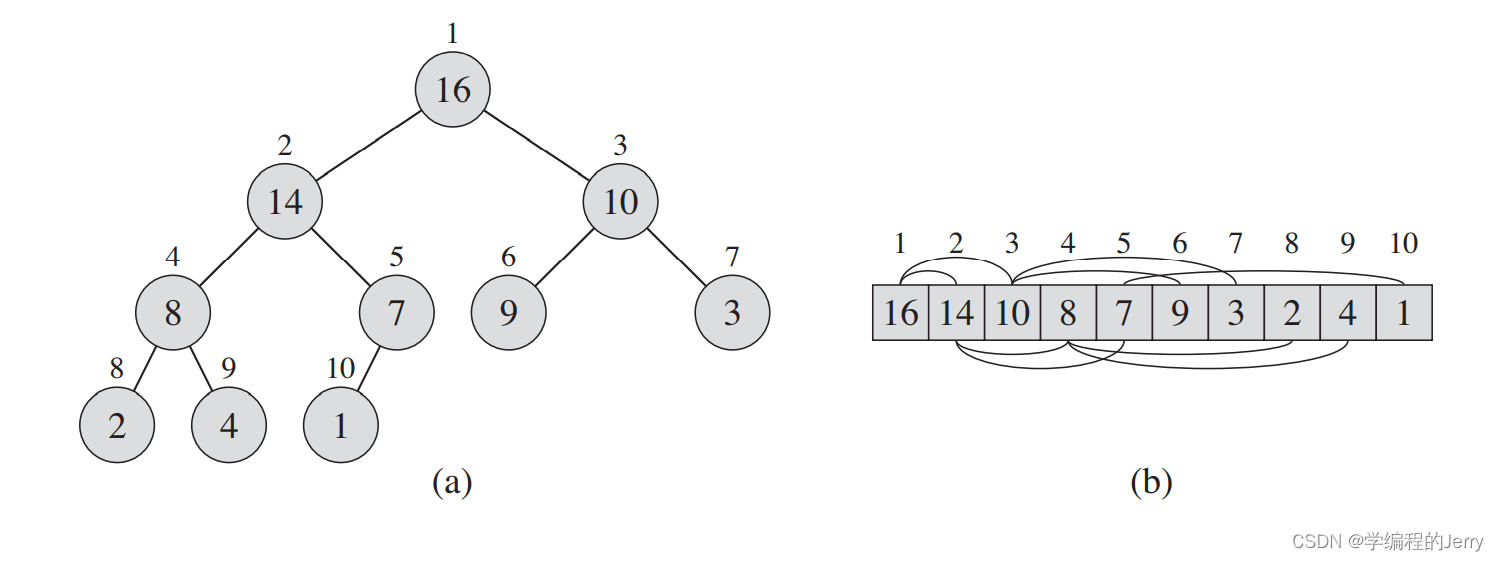
图1（其中1和2、3等构成父子结点，1是根；结点上方的数字表示其下标；在b图中，父结点总是在子结点的左边）

3、使用技巧

（1）如何通过计算得到父结点、左孩子和右孩子：

4、分类

二叉堆可以分为两种形式：最大堆和最小堆，在两种堆中，结点的值都要满足 堆的性质。
（1）最大堆：除了根之外所有元素都要满足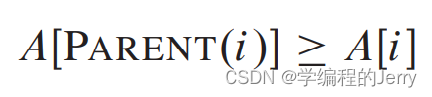

意思就是除了根之外的所有结点的值小于等于父结点的值，那么一个堆中最大的元素就是根结点。
（2）最小堆：除了根之外所有元素都要满足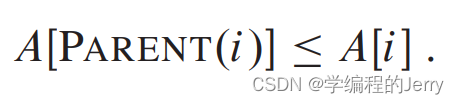

在堆排序算法中，我们往往使用最大堆，最小堆通常用于构造优先队列。

6.2 维护堆的性质

1、MAX-HEAPIFY是用于维护最大堆性质的重要过程。

输入：一个数组A和一个下标i
过程：在调用MAX-HEAPIFY过程中，我们假定根节点LEFT(i)和RIGHT(i)的二叉树都是最大堆，但是我们必须要保证A[i]大于其孩子，我们通过调用这个函数使A[i]可以做到逐级下降。

2、伪代码：

MAX-HEAPIFY(A,i)
//记录A[i]左右子结点的下标
1 l = left(i) 
2 r = right(i)
//如果A[i]的左子结点值大于自己，那么将largest记录为左子结点下标
3 if l <= A.heap-size and A[l] > A[i]
4  	   largest = l
5 else largest = i
//如果A[i]的右子结点值大于自己，那么将largest记录为右子结点下标
6 if r <= A.heap-size and A[r] > A[largest]
7 	   largest = r
//如果largest最后和i不一样，说明A[i]至少小于其一个子结点，那么需要互换值
8 if largest != i
9 	   exchange A[i] with A[largest]
10 	   MAX_HEAPIFY(A,largest)	//以该节点的子树可能会因为上一行而
不满足性质，因此需要进行递归，直到以A[i]为根节点的整个子树满足最大堆性质

3、案例

图2（表示了MAX-HEAPIFY(A,2)的执行过程，（a）中表示初始状态，因为A[2]小于子结点，不符合最大堆的性质。（b）中通过交换A[2]和A[4]的值，但是导致A[4]以下又不符合最大堆的性质。然后递归调用MAX-HEAPIFY(A,4)，此时i=4。（c）中将A[4]和A[9]交换位置，恢复规律，再次递归调用MAX-HEAPTYFY(A,9)，此后数据不变）

4、运行时间分析

对于一棵以i为根结点、大小为n的子树，
（1）调整A[i]、A[LEFT(i)]、A[RIGHT(i)]需要花费θ(1)的时间。
（2）假设递归调用会发生，即在一棵以i的一个孩子为根结点的树上运行MAX-HEAPIFY。
因为每个孩子的子树大小至多是2n/3（最坏情况是最底层半满的时候）。

证明：为什么是2n/3?
前提：二叉堆为完全二叉树，规定总结点数为n，要求根的左子树的最大总结点数
（由于右子树的结点总数<=左子树的结点总数）。
过程：显然，观察最底层节点数目为0, 1, 2...的情况，显然最底层半满的时候左子树达到了最大。
以下求此时左子树的大小：
设底层半满时节点数为x，则再加x个节点就是完全满的树。
满树的总结点数  sum = n + x = 2x * 2 - 1 = 4x - 1 ①	（离散数学知识，p个顶点，t片树叶时，p=2t-1）
可得n = 3x - 1，进而 x =（n+1) / 3  ②
满树时，左子树节点数 = (满树sum - 1) / 2 （满树减掉根结点后左右子树对半分）
代入①②式，得到
 2x -1 = 2n/3 - 1/3 ＜ 2n / 3，最终得证。

那么用下面这个递归式刻画MAX-HEAPIFY的运行时间：
T(n) <= T(2n/3) + Θ(1)
根据之前结论：上式解为T(n) = O(lg n)，因为树高h本质上也是与lg是同一回事，因此MAX-HEAPIFY时间复杂度为O(h)。

6.3 建堆

一、基本内容

1、我们可以使用自底而上的办法利用过程MAX-HEAPIFY把一个大小为n = A.length的数组A[1…n]转换为最大堆。（利用结论：当用数组表示存储n个元素的堆时，叶结点下标分别为⌊n/2⌋+1,⌊n/2⌋+2,…,n）每个叶结点都可以看成只包含一个元素的堆。过程BUILD-MAX-HEAP对树中的其他结点都调用一次MAX-HEAPIFY。
2、伪代码

BUILD-MAX-HEAP(A)
1 A.heap-size = A.length
2 for i = ⌊A.length/2⌋ downto 1
3 		MAX-HEPIFY(A,i)

3、运行时间
（1）不那么紧确的运行时间：每次调用MAX-HEAPIFY的时间复杂度为O(lgn)，BUILD-MAX-HEAP需要O(n)次这样的调用，因此总的时间复杂度为O(n lgn)
（2）更紧确的：利用如下性质得到更加紧确的界：含n个元素的堆的高度为⌊lgn⌋，高度为h的堆最多包含⌈n/2^h+1⌉个结点。
①在一个高度为h的结点上运行MAX-HEAPIFY的代价是O(h),将BUILD-MAX-HEAP的总代价表示为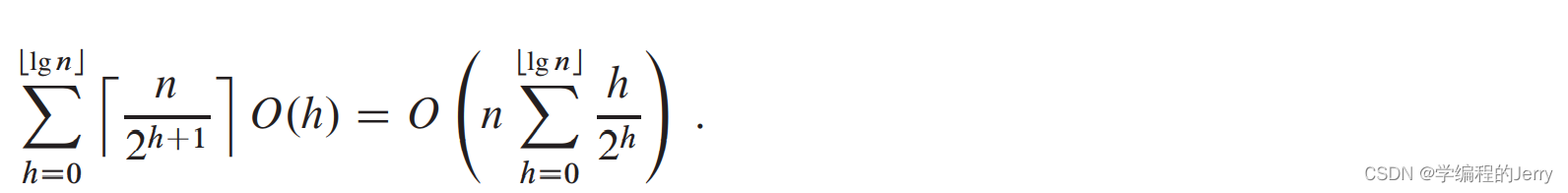

②最后一个累积和的计算可以用x=1/2代入
S(x) = ∑kx^k = x/(1-x)²得到

③于是我们可以知道BUILD-MAX-HEAP的时间复杂度：

二、案例

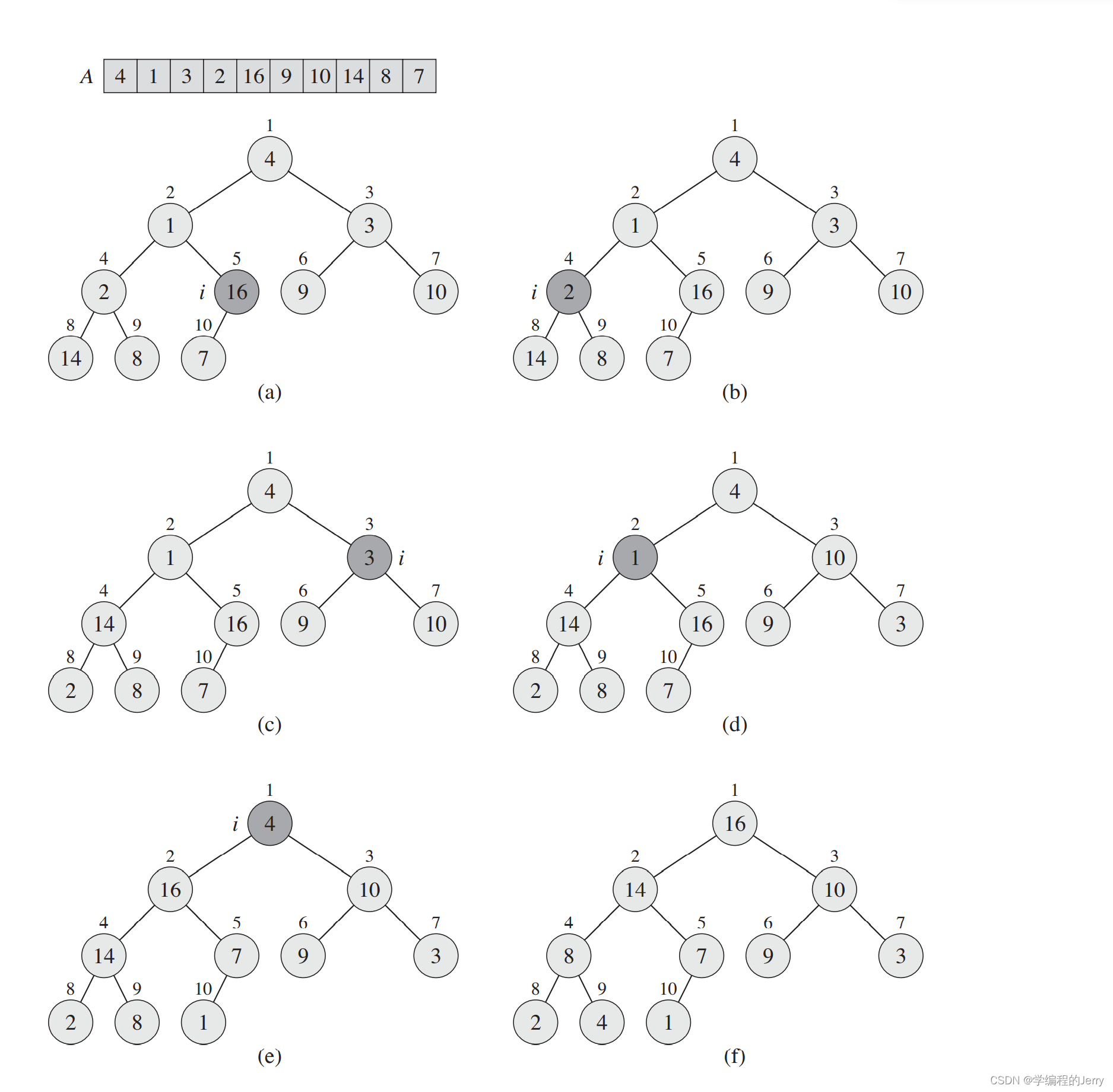
图3 描述了BUILD-MAX-HEAP的操作过程。（a）包括一个输入的数组和一个二叉树，显示调用MAX-HEAPIFY(A,i)之前，i指向结点5的情况。（b）进行一次迭代后，i指向结点4。（c）~（e）BUILD-MAX-HEAP中for循环的后续迭代，注意，在某个结点调用MAX-HEPIFY，该结点的两个子树都是最大堆（虽然过程中可能不是，如d-e）。（f）执行完BUILD-MAX-HEAP形成的最大堆。

三、举一反三

类似的，我们可以通过BUILD-MIN-HEAP构造一个最小堆，除了MAX-HEAP中需要进行微调之外，BUILD-MAX-HEAP不需要变化。