当前位置:网站首页>【学习笔记】AGC010
【学习笔记】AGC010
2022-07-07 10:59:00 【仰望星空的蚂蚁】
多做 AGC 长脑子
不给样例,光靠脑子想
Rearranging
- 考虑如果两个数不互质,那么它们在最终序列相对位置不变
- 因此对两个不互质的数连边,同时对每条边定向构造 DAG
- 答案就是最大的拓扑序,因为考虑一个点没有入度的话可以和任何其他的点交换
- 贪心的构造 。从编号最小的点开始 dfs ,每次找节点编号最小的出边,可以理解成构造了一颗树 。
- 然后模拟就行了 (
Tiling
- 贪心的考虑如何最大限度将网格铺满
- 显然将网格剖分成若干个 2x2 的矩阵是最优的
- 边角料就铺对应的横砖或竖砖
- 这样一定能最大化铺砖的数量
- 手玩发现 n=3,m=3,A=2,B=2 的情况会有问题(这里找 hack 数据是难点
- 也就是说对于最后一个 2x2 的方格,还剩横砖和竖砖各一个,理论上能铺两块砖,但是由于形状原因只能铺一块
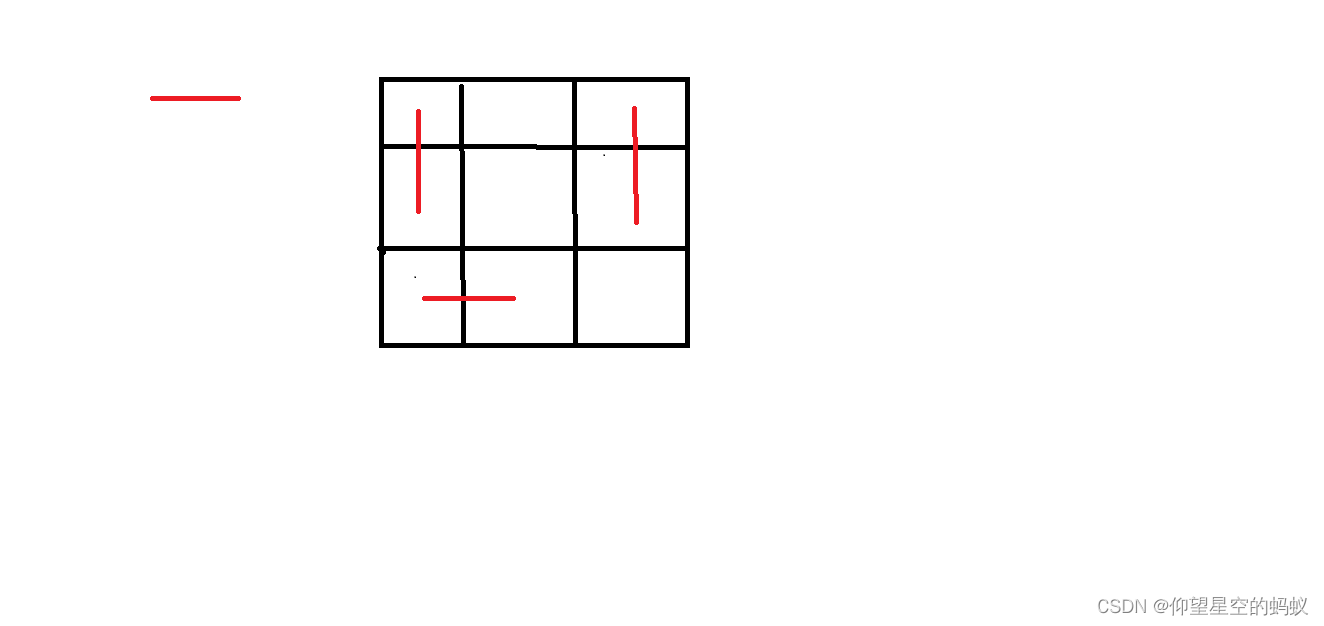
- 注意到右下角还空了一个位置,可以通过调整放下 。
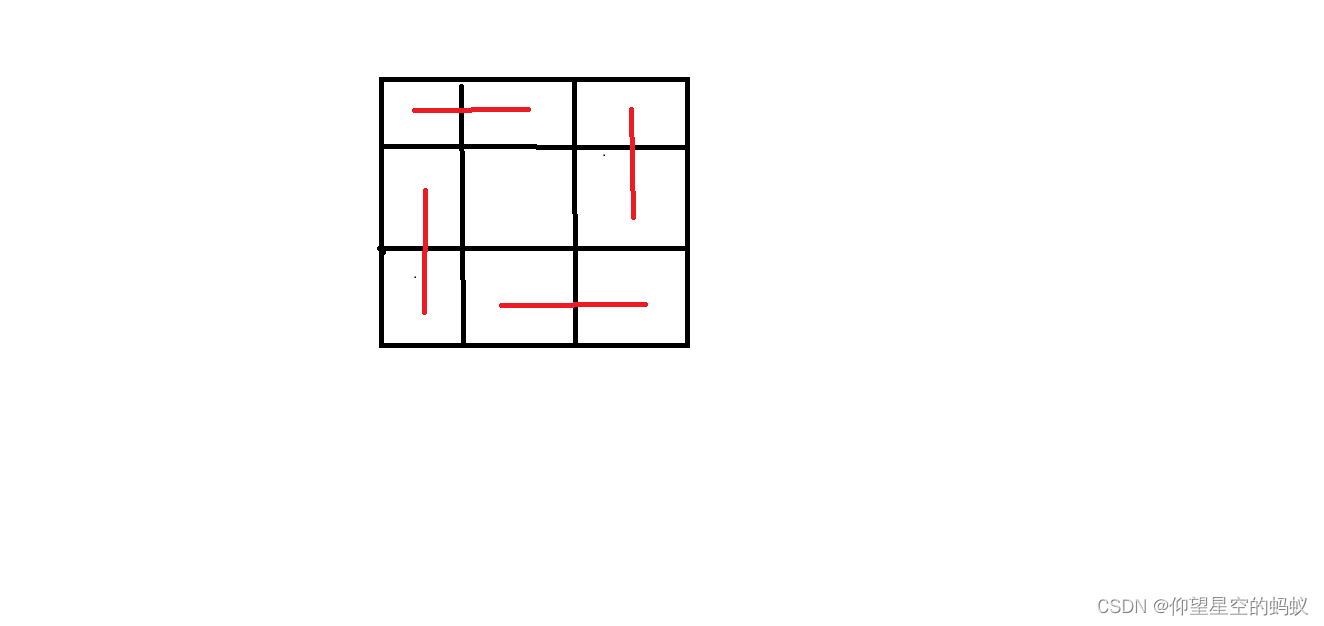
- 直接分两种方案 check 即可 。
- 注意到网格问题 Nastia and a Beautiful Matrix ,从 最大化利用网格空间 入手,找到局部最优,进而构造出全局最优解 。
Three Circuits
- 每个点的度数都必须是偶数
- 题目给了这是一个连通图,所以一定存在欧拉回路
- 如果存在点的度数 >=6 ,那么必然有解(考虑从欧拉回路角度去证
- 记度数 = 4 的点个数为 cnt
- 如果 cnt=0 ,那么最多只能构造出一个环
- 如果 cnt=1 ,那么最多只能构造出两个环
- 如果 cnt=2 ,那么有两种情况(画图感知:可能构造出两个环或三个环
- 如果 cnt>=3 ,那么去掉一个简单环后归纳到 cnt=2 的情况,最少能构造出三个环
Decrementing
- 如果存在 a i = 1 a_i=1 ai=1 ,那么判断 ∑ ( a i − 1 ) \sum{(a_i-1)} ∑(ai−1) 的奇偶性 。
- 定义 ∑ ( a i − 1 ) \sum{(a_i-1)} ∑(ai−1) 奇数时为胜态,偶数时为负态
- 如果当前正在操作的人为胜态,那么无论另一个人怎么操作,当前这个人必胜
- 因为考虑如果没有所有数都除以最大公约数这个操作的话, ∑ a i \sum a_i ∑ai 的奇偶性不会变化,那么 ∑ ( a i − 1 ) \sum (a_i-1) ∑(ai−1) 的奇偶性也不会变化,胜负态是固定的
- 现在相当于 ∑ a i → ∑ a i x \sum{a_i}\to \frac{\sum{a_i}}{x} ∑ai→x∑ai ,当且仅当 x x x 是偶数且 ∑ a i x \frac{\sum{a_i}}{x} x∑ai 为奇数时才行
- 记序列中奇数的个数为 cnt ,初始因为互质所以 cnt>=1 ,那么两个人轮流操作,后手的人永远无法让 cnt=0 (n>=3 时)
- 如果当前操作的人为败态,那就操作唯一的奇数,这样有可能逆转胜负 。
- 因此直接模拟 。最多不会超过 log a \log a loga 次 。
边栏推荐
- Day21 multithreading
- 高瓴投的澳斯康生物冲刺科创板:年营收4.5亿 丢掉与康希诺合作
- Leetcode skimming: binary tree 25 (the nearest common ancestor of binary search tree)
- layer弹出层的关闭问题
- ISPRS2021/遥感影像云检测:一种地理信息驱动的方法和一种新的大规模遥感云/雪检测数据集
- 聊聊Redis缓存4种集群方案、及优缺点对比
- Lingyunguang of Dachen and Xiaomi investment is listed: the market value is 15.3 billion, and the machine is implanted into the eyes and brain
- 【无标题】
- 详解ThinkPHP支持的URL模式有四种普通模式、PATHINFO、REWRITE和兼容模式
- Ip2long and long2ip analysis
猜你喜欢
处理链中断后如何继续/子链出错removed from scheduling
Charles: four ways to modify the input parameters or return results of the interface

关于 appium 如何关闭 app (已解决)
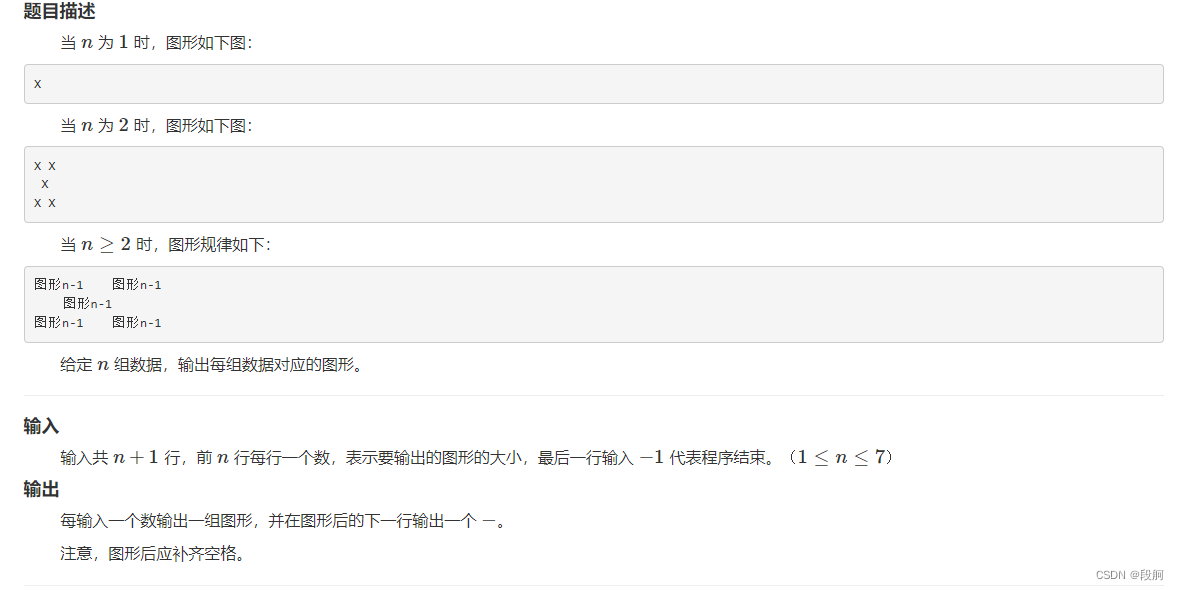
HZOJ #240. Graphic printing IV

《开源圆桌派》第十一期“冰与火之歌”——如何平衡开源与安全间的天然矛盾?

Awk of three swordsmen in text processing

Leetcode brush questions: binary tree 19 (merge binary tree)
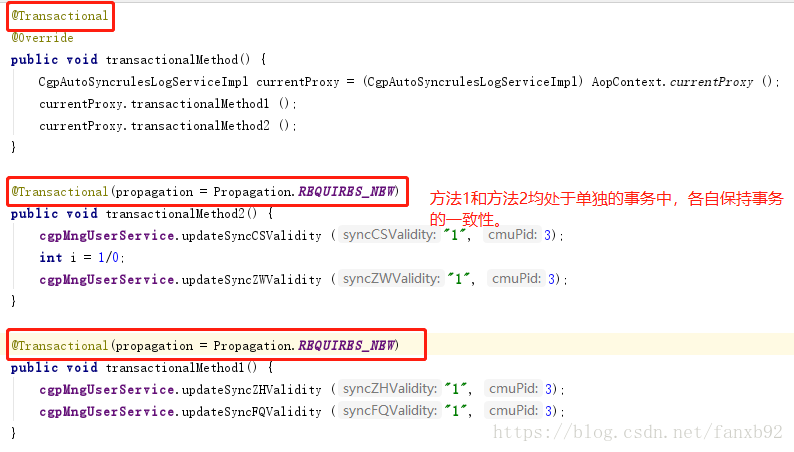
How to apply @transactional transaction annotation to perfection?
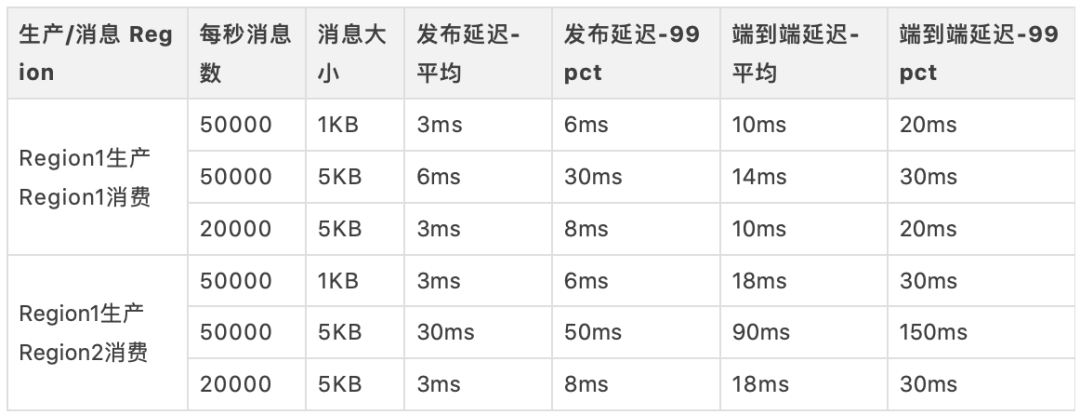
Blog recommendation | Apache pulsar cross regional replication scheme selection practice
Creation and assignment of graphic objects
随机推荐
[statistical learning method] learning notes - support vector machine (Part 2)
飞桨EasyDL实操范例:工业零件划痕自动识别
[learn micro services from 0] [02] move from single application to service
test
Simple implementation of call, bind and apply
有什么类方法或是函数可以查看某个项目的Laravel版本的?
Session
HZOJ #240. 图形打印四
图形对象的创建与赋值
【无标题】
Several ways to clear floating
[binary tree] delete points to form a forest
达晨与小米投的凌云光上市:市值153亿 为机器植入眼睛和大脑
. Net ultimate productivity of efcore sub table sub database fully automated migration codefirst
Leetcode brush question: binary tree 24 (the nearest common ancestor of binary tree)
.Net下極限生產力之efcore分錶分庫全自動化遷移CodeFirst
PHP调用纯真IP数据库返回具体地址
3D content generation based on nerf
详解ThinkPHP支持的URL模式有四种普通模式、PATHINFO、REWRITE和兼容模式
2022-07-07 Daily: Ian Goodfellow, the inventor of Gan, officially joined deepmind