[statistical learning method] learning notes - logistic regression and maximum entropy model

The return of logic （logistic regression） It is a classic classification method in statistical learning . Maximum entropy is a criterion for probabilistic model learning , It is extended to the classification problem to obtain the maximum entropy model （maximum entropy model）. Logistic regression model and maximum entropy model belong to logarithmic linear model .

1. Logistic regression model

1.1 Logistic distribution （logistic distribution）

Definition （ Logistic distribution ） set up X obey continuity A random variable ,X Obeying the logistic distribution means X Have the following Distribution function and Density function ：
$$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu )/r}}$$
$$f(x)=F^{\prime }(x)=\frac{e^{-(x-\mu )/r}}{\gamma (1+e^{-(x-\mu )/r}{)}^2}$$
among ,$\mu$ For position parameters ,$\gamma >0$ For shape parameters .
Density function of logistic distribution $f(x)$ And distribution function $F(x)$ The figure of is shown in the figure below .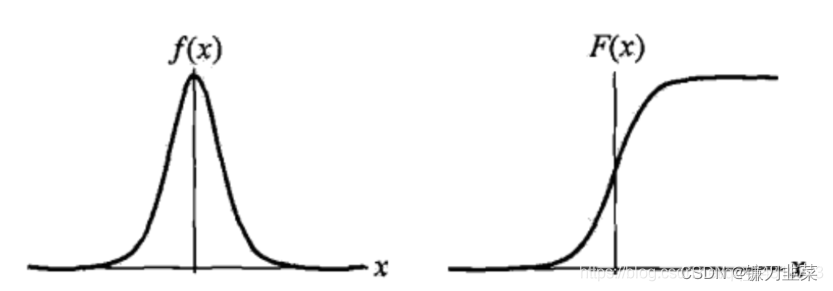

Distribution function belongs to logistic function , Its figure belongs to a S Shape curve （sigmoid curve）. The curve is in point $(\mu ,\frac{1}{2})$ It's central symmetry , The meet
$$F(-x+\mu )-\frac{1}{2}=-F(x+\mu )+\frac{1}{2}$$
The curve grows faster near the center , Slow growth at both ends . shape parameter $\gamma$ The smaller the value of , The faster the curve grows near the center .

1.2 Binomial logistic regression （binomial logistic regression model）

Binomial logistic regression is a classification model , By conditional probability distribution $P(Y|X)$ Express , In the form of parameterized logistic distribution . Here are random variables X The value is a real number , A random variable Y The value is 1 perhaps 0.
Definition （ Logistic regression model ）： Binomial logistic regression model is the following conditional probability distribution ：
$$P(Y=1|x)=\frac{exp(w\cdot x+b)}{1+exp(w\cdot x+b)}$$
$$P(Y=0|x)=\frac{1}{1+exp(w\cdot x+b)}$$
here ,$x\in R^n$ It's input ,$Y\in 0,1$ It's output ,$w\in R^n$ and $b\in R$ Is the parameter ,$wcallbypowervaluetowardsThe\; amount$, $b$ For bias ,$w\cdot x$ by w and x Inner product .
Logistic regression compares two conditional probability values , Will instance x To the category with higher probability value .
Sometimes for convenience , The weight vector and input vector are extended , Still recorded as w,x namely $w=(w^{(1)},w^{(2)},...,w^{(n)},b{)}^T,x=(x^{(1)},x^{(2)},...,x^{(n)},1{)}^T$, be ：
$$P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}$$
$$P(Y=0|x)=\frac{1}{1+exp(w\cdot x)}$$

The characteristics of logistic regression . The probability of an event （odds） It refers to the ratio of the probability of the event occurring to the probability of the event not occurring . If the probability of the event is p, Then the probability of this event is $\frac{p}{1-p}$, The logarithmic probability of the event （log odds） or logit The function is ：
$$logit(p)=log\frac{p}{1-p}$$
For logistic regression , Available ：
$$log\frac{P(Y=1|x)}{1-P(Y=1|x)}=w\cdot x$$
That is to say , In the logistic regression model , Output Y=1 The logarithmic probability of is the input x The linear function of . Or say , Output Y=1 The logarithmic probability of is determined by the input x A model represented by a linear function , Logistic regression model . The closer the value of a linear function approaches positive infinity , The probability value is close to 1; The closer the value of a linear function is to negative infinity , The closer the probability value is to 0.

1.3 Estimation of model parameters

For a given set of training data $T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$, among $x_i\in R^n,y_i\in \{0,1\}$, The maximum likelihood estimation method can be used to estimate the model parameters , So we can get logistic regression model .
set up ：$P(Y=1|x)=\pi (x)$,$P(Y=0|x)=1-\pi (x)$, The likelihood function is :
$$\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}$$
The log likelihood function is ：
$$L(w)=\sum _{i=1}^N[y_i(w\cdot x_i)-\log (1+exp(w\cdot x_i))]$$
Yes $L(w)$ Find the maximum , obtain w The estimate of .
In this way, the problem becomes an optimization problem with log likelihood function as the objective function . The commonly used methods in logistic regression learning are gradient descent method and quasi Newton method .

hypothesis $w$ The maximum likelihood estimate of is $\hat{w}$, Then the learned logistic regression model is ：
$$P(Y=1|x)=\frac{exp(\hat{w}\cdot x)}{1+exp(\hat{w}\cdot x)}$$
$$P(Y=0|x)=\frac{1}{1+exp(\hat{w}\cdot x)}$$

1.4 Multiple logistic regression (multi-nominal logistic regression model)

Suppose a discrete random variable Y The set of values for is {1,2,…, K}, So the multiple logistic regression model is ：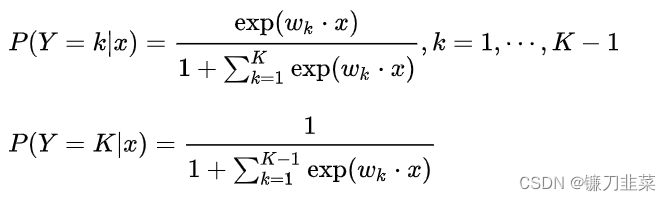

2. Maximum entropy model （maximum entropy model）

The maximum entropy model is derived from the principle of maximum entropy .

2.1 The principle of maximum entropy

The maximum entropy principle is a criterion for probabilistic model learning . Think , When learning probability models , In all possible probability models （ Distribution ） in , The model with the largest entropy is the best model . The set of probabilistic models is usually determined by constraints . therefore , The maximum entropy principle can also be described as selecting the model with the maximum entropy from the set of models that meet the constraints .
Then why choose maximum entropy ？ Because without knowing any information , We can only assume that the data is relatively average in all values , That is, the degree of chaos is the greatest .
Assumed discrete random variable X The probability distribution of $P(X)$, Then its entropy is
$$H(P)=-\sum _{x}P(x)log(x)$$
Entropy satisfies the following inequality ：
$$0\le H(P)\le \log |X|$$
among ,$|X|$ yes X The number of values , If and only if X The equal sign on the right holds when the distribution of is uniform , That is to say, when X When the distribution is uniform , Entropy is maximum .

With this constraint , In the absence of other information ,, It can be said that A and B It's equal probability ,C、D and E It's equal probability , therefore ：
$$P(A)=P(B)=\frac{3}{20}$$
$$P(C)=P(D)=P(E)=\frac{7}{20}$$

2.2 The definition of the maximum entropy model

Suppose the classification model is a conditional probability distribution $P(Y|X)$,$X\in \mathcal{X}\in {\mathbf{R}}^n$ Indicates input ,$Y\in \mathcal{Y}$ Indicative output ,$\mathcal{X}$ and $\mathcal{Y}$ Are the set of input and output respectively . This model represents for a given input $X$, With conditional probability $P(Y|X)$ Output $Y$. Given a training data set $T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$, The goal of learning is to use the maximum entropy principle to select the best classification model .

Given the training data set , We can determine the joint distribution $P(X,Y)$ Empirical distribution and marginal distribution $P(X)$ The distribution of experience , Respectively by $\tilde{P}(X,Y)$ and $\tilde{P}(X)$ Express ：
$$\tilde{P}(X=x,Y=y)=\frac{\nu (X=x,Y=y)}{N}$$
$$\tilde{P}(X=x)=\frac{\nu (X=x)}{N}$$
In style $\nu (X=x,Y=y)$ Represents the sample in the training data $(x,y)$ Frequency of occurrence ,$\nu (X=x)$ Indicates input during training $x$ Frequency of occurrence ,N Represents the training sample size . Then use a characteristic function (feature function)$f(x,y)$ Description input $x$ And the output $y$ A fact between . Its definition is ：
$$f(x,y)=\{\begin{array}{cc}1,& xandyfullfootsomeOnethingsreal\\ 0,& nobe\end{array}$$

The characteristic function $f(x,y)$ About the distribution of experience $\tilde{P}(X,Y)$ The expectation of ：
$$E_{\tilde{P}}(f)=\sum _{x,y}\tilde{P}(x,y)f(x,y)$$

The characteristic function $f(x,y)$ About the model $P(Y|X)$ And experience distribution $\tilde{P}(X,Y)$ The expectation of ：
$$E_P(f)=\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)$$

If the model can get the information in training , Then we can assume that the two expectations are equal , namely ：
$$E_{\tilde{P}}(f)=E_P(f)$$
namely ：
$$\sum _{x,y}\tilde{P}(x,y)f(x,y)=\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)$$
The above formula is the constraint condition of model learning .

Maximum entropy model Suppose that the set of models satisfying all the constraints is ：
$$\mathcal{C}=\{P\in \mathcal{P}|E_P(f_i)=E_{\tilde{P}}(f_i),i=1,2,...,n\}$$
Defined in conditional probability distribution $P(Y|X)$ The conditional entropy on is ：
$$H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$$
Then the model set $\mathcal{C}$ Medium conditional entropy $H(P)$ The largest model is called the maximum entropy model .

2.3 Learning the maximum entropy model

The learning process of the maximum entropy model is The process of solving the maximum entropy model , It can also be formalized as a constrained optimization problem . Given the training data set $T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$ And the characteristic function $f_i(x,y),i=1,2,...n$, The learning of the maximum entropy model is equivalent to the constrained optimization problem ：
$$\underset{P\in \mathcal{C}}{\max }H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$$
$$s.t.E_P(f_i)=E_{\tilde{P}}(f_i),i=1,2,...,n\sum _{y}P(y|x)=1$$

According to the habit of optimization problems , We Transform the problem of finding the maximum value into an equivalent problem of finding the minimum value ：
$$\underset{P\in \mathcal{C}}{\min }-H(P)=\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$$
$$s.t.E_P(f_i)=E_{\tilde{P}}(f_i),i=1,2,...,n\sum _{y}P(y|x)=1$$
here , The original problem of constrained optimization is transformed into the dual problem of unconstrained optimization . Solve the original problem by solving the dual problem .
For the above optimization problem , First , Introduce Lagrange multipliers $w_0,w_1,...,w_n$, Define the Lagrange function $L(P,w)$：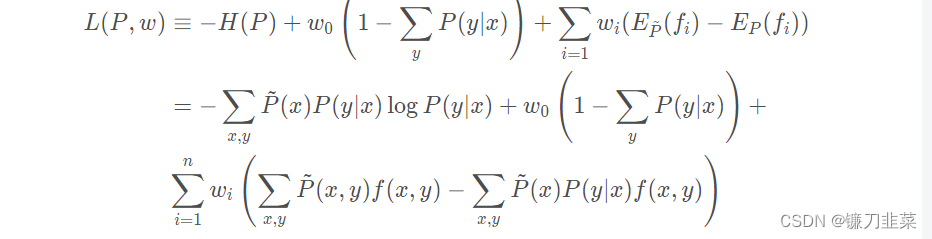

The original problem of optimization is ：
$$\underset{P\in \mathbf{C}}{\min }\underset{w}{\max }L(P,w)$$
The dual problem is ：
$$\underset{w}{\max }\underset{P\in \mathbf{C}}{\min }L(P,w)$$
Because of the Lagrange function $L(P,w)$ yes P The convex function of , The solution of the primal problem is equivalent to the solution of the dual problem . In this way, the original problem can be solved by solving the dual problem .
First, solve the internal minimization problem $\underset{P\in \mathbf{C}}{\min }L(P,w)$, Write it down as ：
$$\Psi (w)=\underset{P\in \mathbf{C}}{\min }L(P,w)=L(P_w,w)$$
$\Psi (w)$ It's called a dual function . meanwhile , Put it down as ：
$$P_w=\arg \underset{P\in \mathbf{C}}{\min }L(P,w)=P_w(y|x)$$
Then seek $L(P,w)$ Yes $P(y|x)$ Partial derivative of ：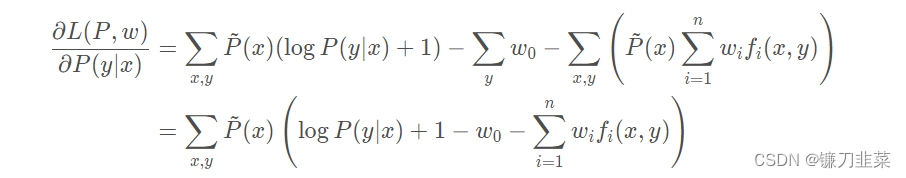

Let the partial derivative be equal to 0 And in $\tilde{P}(x)>0$ Under the circumstances , Solution ：
$$P(y|x)=\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)+w_0-1\right)=\frac{\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)}{\exp (1-w_0)}$$
Due to constraints $\sum _{y}P(y|x)=1$, have to （ Here is based on and 1 Replace the denominator in the above formula with ）：
$$P_w(y|x)=\frac{1}{Z_w(x)}\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$
among ：
$$Z_w(x)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$
$Z_w(x)$ It's called normalization factor ;$f_i(x,y)$ It's a characteristic function ;$w_i$ It's the weight of the feature .
after , Solve the maximization problem outside the dual problem ：
${\max }_w\Psi (w)$
Put it down as $w^{\ast }$, namely ：
$w^{\ast }=\arg {\min }_w\Psi (w)$

2.3 Maximum likelihood estimation

The maximization of dual function is equivalent to the maximum likelihood estimation of maximum entropy model . Prove slightly .
The maximum entropy model has a similar form to the logistic regression model , They are also called log linear models （log linear model）. Model learning is the maximum likelihood estimation or regularized maximum likelihood estimation of the model under the given training data conditions .

3. Optimization algorithms for model learning

Logistic regression model 、 The learning of maximum entropy model is reduced to the optimization problem with likelihood function as the objective function , Usually by iterative algorithm solve . At this time, the objective function is smooth Convex function , Common methods have improved Iterative scaling 、 Gradient descent method 、 Newton method and Quasi Newton method etc. . Newton method or quasi Newton method generally converges faster .

3.1 The improved iterative scaling method （improved iterative scaling, IIS）

IIS It is an optimization algorithm for maximum entropy model learning . The known maximum entropy model is ：
$$P_w(y|x)=\frac{1}{Z_w(x)}\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$
among ：
$$Z_w(x)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$
The log likelihood function is （ Derivation is omitted here ）：
$$\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{w}_i{f}_i(x,y)-\sum _x\tilde{P}(x)\log Z_w(x)$$

The goal is to learn model parameters by maximum likelihood estimation , That is to find the maximum of the log likelihood function $\hat{w}$. The idea of the improved iterative scaling method is ：== Suppose that the current parameter vector of the maximum entropy model is $w=(w_1,w_2,...,w_n{)}^{\mathrm{T}}$, We want to find a new parameter vector $w+\delta =(w_1+\delta ,w_2+\delta ,...,w_n+\delta {)}^{\mathrm{T}}$, Make the log likelihood function of the model increase . If there is such a method of updating parameter vectors $\tau :w\to w+\delta$, Then you can reuse this method , Until the maximum value of the log likelihood function is found . For a given empirical distribution $\tilde{P}(x,y)$, Model parameters from $w$ To $w+\delta$, The variable of log likelihood function is ：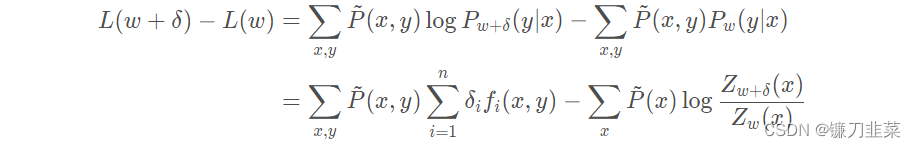

Using inequality ：
$$-log\alpha \ge 1-\alpha ,\alpha >0$$
Establish the lower bound of the variable of the log likelihood function ：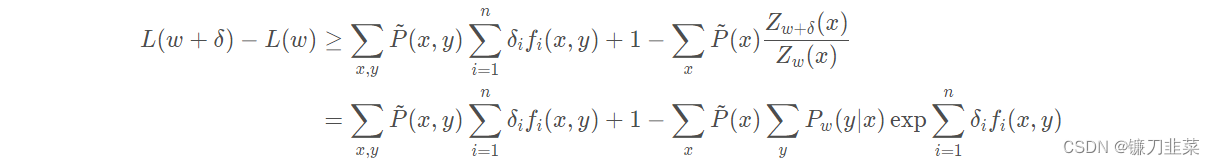

Mark the right end of the above formula as $A(\delta |w)$, namely ：
$$L(w+\delta )-L(w)\ge A(\delta |w)$$
namely $A(\delta |w)$ Is a lower bound of the variable of the log likelihood function . If you can find the right $\delta$ Raise the lower bound , Then the log likelihood function will also improve . However , function $A(\delta |w)$ Medium $\delta$ It's a vector , Contains multiple variables , Not easy to optimize at the same time . The improved iterative scaling method attempts to optimize only one of the variables ${\delta }_i$, And fix other variables ${\delta }_j,i\ne j$.

For this purpose , The improved iterative scaling method further reduces the lower bound . In particular , Introduce a quantity $f^{\#}(x,y)$：
$$f^{\#}(x,y)=\sum _i{f}_i(x,y)$$
because $f_i$ Is a binary function , so $f^{\#}(x,y)$ Indicates that all features are in $(x,y)$ Number of occurrences . such ,$A(\delta |w)$ to ：
$$A(\delta |w)=\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\sum _y{P}_w(y|x)\exp \left(f^{\#}(x,y)\sum _{i=1}^n\frac{{\delta }_i{f}_i(x,y)}{f^{\#}(x,y)}\right)\text{\hspace{1em}(12)}$$
According to the definition ,$f_i(x,y)$ It means the first one $i$ Characteristic in $(x,y)$ Number of occurrences ;$f^{\#}(x,y)$ Indicates that all features are in $(x,y)$ Number of occurrences . So there is ：
$$\frac{f_i(x,y)}{f^{\#}(x,y)}\ge 0,\sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}=1$$
according to Jensen inequality ：
$$f\left({\lambda }_i\sum _{i=1}^{n}f(x_i)\le \sum _{i=1}^n{\lambda }_{i}f(x_i)\right)$$
So there is ：
$$\exp \left(\sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}{\delta }_i{f}^{\#}(x,y)\right)\le \sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}\exp \left({\delta }_i{f}^{\#}(x,y)\right)$$
thus , type （11） I could rewrite it as ：
$$A(\delta |w)\ge \sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\sum _y{P}_w(y|x)\sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}\exp \left({\delta }_i{f}^{\#}(x,y)\right)$$
Remember that the right end of the equation is $B(\delta |w)$, So I got ：
$$L(w+\delta )-L(w)\ge B(\delta |w)$$
there $B(\delta |w)$ A new lower bound of the variable of logarithmic likelihood function . seek $B(\delta |w)$ Yes ${\delta }_i$ Partial derivative of ：
$$\frac{\partial B(\delta |w)}{\partial {\delta }_i}=\sum _{x,y}\tilde{P}(x,y)f_i(x,y)-\sum _x\tilde{P}(x)\sum _y{P}_w(y|x)f_i(x,y)\exp \left({\delta }_i{f}^{\#}(x,y)\right)$$
Let the partial derivative be equal to 0, Yes ：
$$\sum _{x,y}\tilde{P}(x)P_w(y|x)f_i(x,y)\exp \left({\delta }_i{f}^{\#}(x,y)\right)=E_{\tilde{P}}(f_i)$$
therefore , In turn ${\delta }_i$ Solve the equation to find $\delta$.

Algorithm （ Improved iterative scaling algorithm IIS）

3.2 Quasi Newton method

For the maximum entropy model ：
$$P_w(y|x)=\frac{\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)}{\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)}$$

Objective function ：
$$\underset{w\in {\mathbf{R}}^n}{\min }f(w)=\sum _x\tilde{P}(x)\log \sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)-\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{w}_i{f}_i(x,y)$$

gradient ：
$$g(w)={\left(\frac{\partial f(w)}{\partial w_1},\frac{\partial f(w)}{\partial w_2},...,\frac{\partial f(w)}{\partial w_n}\right)}^{\mathrm{T}}$$

among ：
$$\frac{\partial f(w)}{\partial w_i}=\sum _{x,y}\tilde{P}(x)P_w(y|x)f_i(x,y)-E_{\tilde{P}}(f_i),i=1,2,...,n$$

Algorithm （ Quasi Newton method for maximum entropy model learning ）

4. summary

• Logistic regression model can be used to classify two or more classes .
• Logistic regression model is a logarithmic probability model of output expressed by linear function of input .
• The principle of maximum entropy is a criterion for learning or estimating probabilistic models .
• The maximum entropy principle holds that in all possible probability models （ Distribution ） The collection of , The model with the largest entropy is the best model .
• Logistic regression model and maximum entropy model are both logarithmic linear models .
• The learning of logistic regression model and maximum entropy model generally adopts maximum likelihood estimation , Or regularized MLE .
• The learning of logistic regression model and maximum entropy model can be formalized as unconstrained optimization problem . The algorithm for solving this problem is the improved iterative scaling method 、 Gradient descent method 、 Quasi Newton method .

5. Content sources

[1] 《 Statistical learning method 》 expericnce