当前位置:网站首页>Master公式。(用于计算递归的时间复杂度。)
Master公式。(用于计算递归的时间复杂度。)
2022-07-07 10:33:00 【Kinght_123】

一、Mster公式

前提条件:
- 递归的子问题的规模必须是相同的。
下面让我来解释一下,这个公式具体的含义。
首先a是一个递归问题的子问题的规模的调用次数,d是子问题的数目,后面的N的d次方就是除了递归子问题的调用,其他问题规模的时间复杂度。
举个例子:
def func(arr, l, r): # 再arr数组中找到最大的数值
if l == r:
return arr[l]
mid = l + ((r - l) >> 1)
l_max = func(arr, l, mid)
r_max = func(arr, mid + 1, r)
return max(l_max, r_max)
比如上面的代码就是一个简单的递归。
那么的它的T(N) = 2 * T(N / 2) + O(1)
因为每次调用主函数,需要调用两次规模相同的子问题的函数,所以为2 * T(N / 2),又因为它除了调用子问题的函数,其他的时间复杂度为O(1).所以这就是这个递归的Master公式。
二、计算时间复杂度

按照这个公式和我们上面的代码,时间复杂度应该为O(N)
边栏推荐
- Static routing assignment of network reachable and telent connections
- Dialogue with Wang Wenyu, co-founder of ppio: integrate edge computing resources and explore more audio and video service scenarios
- When OSPF specifies that the connection type is P2P, it enables devices on both ends that are not in the same subnet to Ping each other
- 2022聚合工艺考试题模拟考试题库及在线模拟考试
- [statistical learning methods] learning notes - Chapter 5: Decision Tree
- 广州市召开安全生产工作会议
- 普乐蛙小型5d电影设备|5d电影动感电影体验馆|VR景区影院设备
- 图形对象的创建与赋值
- GCC compilation error
- 【统计学习方法】学习笔记——支持向量机(上)
猜你喜欢

【统计学习方法】学习笔记——支持向量机(上)

SQL lab 11~20 summary (subsequent continuous update) contains the solution that Firefox can't catch local packages after 18 levels
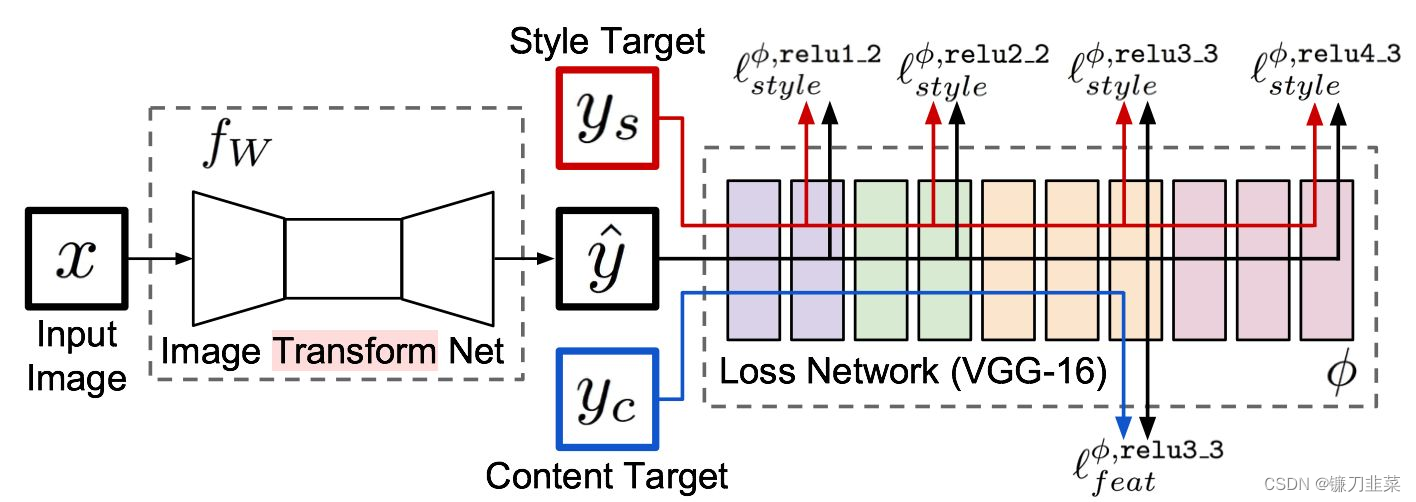
【PyTorch实战】用PyTorch实现基于神经网络的图像风格迁移
Multi row and multi column flex layout
![[爬虫]使用selenium时,躲避脚本检测](/img/3a/85ea729be2aa76c3de4a822ca6939b.png)
[爬虫]使用selenium时,躲避脚本检测

<No. 9> 1805. Number of different integers in the string (simple)
![[statistical learning methods] learning notes - Chapter 5: Decision Tree](/img/0e/c60e04ab4a7ae4728cc76eff1c028a.png)
[statistical learning methods] learning notes - Chapter 5: Decision Tree
![[pytorch practice] image description -- let neural network read pictures and tell stories](/img/39/b2c61ae0668507f50426b01f2deee4.png)
[pytorch practice] image description -- let neural network read pictures and tell stories
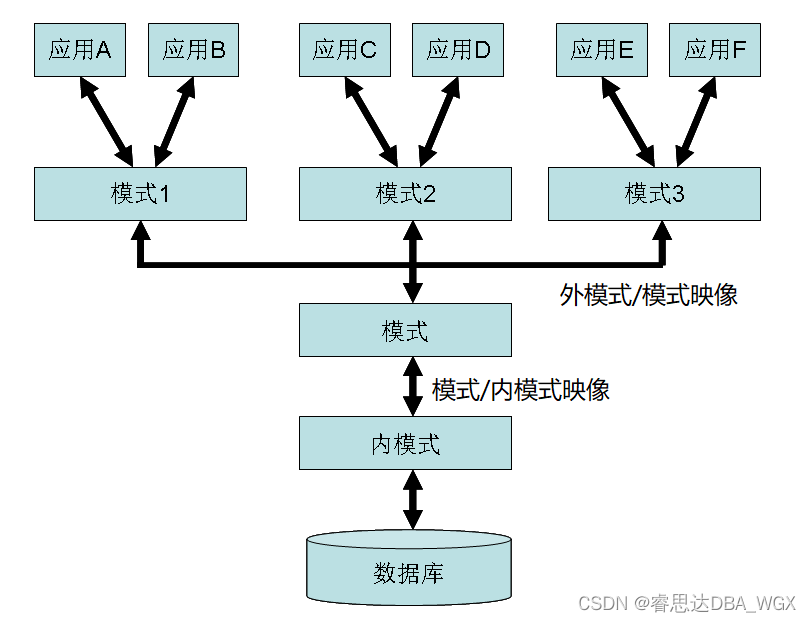
Tutorial on principles and applications of database system (007) -- related concepts of database
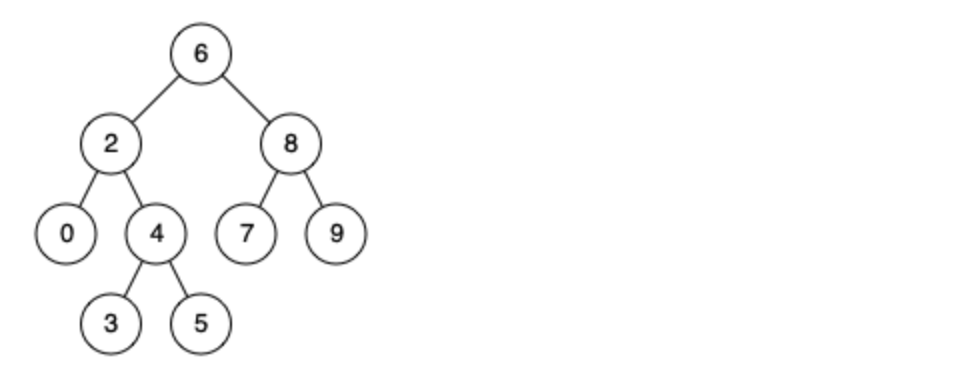
leetcode刷题:二叉树25(二叉搜索树的最近公共祖先)
随机推荐
Attack and defense world - PWN learning notes
【从 0 开始学微服务】【01】什么是微服务
[pytorch practice] use pytorch to realize image style migration based on neural network
Financial data acquisition (III) when a crawler encounters a web page that needs to scroll with the mouse wheel to refresh the data (nanny level tutorial)
【从 0 开始学微服务】【02】从单体应用走向服务化
[statistical learning method] learning notes - support vector machine (I)
SQL lab 26~31 summary (subsequent continuous update) (including parameter pollution explanation)
MPLS experiment
2022聚合工艺考试题模拟考试题库及在线模拟考试
idm服务器响应显示您没有权限下载解决教程
【从 0 开始学微服务】【03】初探微服务架构
2022A特种设备相关管理(锅炉压力容器压力管道)模拟考试题库模拟考试平台操作
VSCode的学习使用
Object. Simple implementation of assign()
About web content security policy directive some test cases specified through meta elements
SQL Lab (36~40) includes stack injection, MySQL_ real_ escape_ The difference between string and addslashes (continuous update after)
sql-lab (54-65)
[statistical learning method] learning notes - support vector machine (Part 2)
牛客网刷题网址
Vxlan static centralized gateway