当前位置:网站首页>complete knapsack problem
complete knapsack problem
2022-08-03 10:49:00 【hnjzsyjyj】
【题目来源】
https://www.acwing.com/problem/content/description/3/
【问题描述】
有 N 种物品和一个容量是 V 的背包,每种Items are无限件可用.
第 i 种物品的体积是 vi,价值是 wi.
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大.
输出最大价值.
【输入格式】
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积.
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 种物品的体积和价值.
【输出格式】
输出一个整数,表示最大价值.
【数据范围】
0<N,V≤1000
0<vi,wi≤1000
【算法分析】
背包问题,求解的是“将Some kind of物品装入背包,......”,而不是求解“将某些个物品装入背包,......”的问题.切记.
完全背包问题,类似于0-1背包问题,Still is solving“将What kind of物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大”.Therefore, still can set c[i][j] 为将前 i Kind of goods loading capacity of j 的背包中所获得的最大价值,vol[i] 为第 i The volume of goods,val[i] 为第 i 种物品的价值.但由于其特殊性,In completely knapsack problem of each item in无限多个,而0-1Each items from the knapsack problem is一个,Therefore, in using the“最后一步法”To build fully knapsack problem when the state transition equation,针对第 i 种物品,可能会选择0,1,2,... ,k个(k*vol[i]<=j).Are selected to k 个,Rather than an unlimited number of,The reason is that even though the knapsack problem completely each item has an unlimited number of,But is limited by a knapsack capacity,Can hold only a finite number of.
Knapsack problem completely video interpretation refer:https://www.bilibili.com/video/BV16F411M7CU
Ideas as shown in the figure below:

Visible on the basis of the analysis of the above ideas,Code is completely knapsack problem will have a triple loop,Bound to lead to code complexity increases.同时,It also will inevitably lead to time complexity increase,有可能会TLE.因此,需要进行优化.
Will completely knapsack problem of state transition equation is written in the below:
c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i], ..., c[i-1][j-(k-1)*vol[i]]+(k-1)*val[i], c[i-1][j-k*vol[i]]+k*val[i]),
令 j=j-vol[i],并考虑到 k*vol[i]<=j,则有
c[i][j-vol[i]]=max(c[i-1][j-vol[i]],c[i-1][j-vol[i]-vol[i]]+val[i], ..., c[i-1][j-vol[i]-(k-1)*vol[i]]+(k-1)*val[i])
=max(c[i-1][j-vol[i]],c[i-1][j-2*vol[i]]+val[i], ..., c[i-1][j-k*vol[i]]+(k-1)*val[i])
Launched completely knapsack problem of state transition equation c[i][j]=max(c[i-1][j], c[i][j-vol[i]]+val[i]),This optimization for 2 d.
类比于0-1背包问题的状态转移方程 c[i][j]=max(c[i-1][j],c[i-1][j-vol[i]]+val[i]) Optimization for one dimensional thinking,But on the basis of the above optimization for 2 d,Further completely knapsack problem come to the one dimensional optimization form:
c[j]=max(c[j], c[j-vol[i]]+val[i]),满足 i:1~n,j:1~V 且 j>=vol[i]
If it is from the point of view of the code template,Completely knapsack problem code only needs to be0-1Knapsack problem of one-dimensional implementation code of the inner loop instead of from vol 到 V To traverse the can.即将0-1Knapsack problem of one-dimensional implementation中的内层循环 for(int j=V;j>=vol;j--) 改为 for(int j=vol;j<=V;j++) ,For full backpack code.Isn't it a bit of a wasteO(∩_∩)O哈哈~
【算法代码】
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
int c[maxn];
int main() {
int n,V;
cin>>n>>V;
for(int i=1;i<=n;i++){
int vol,val;
cin>>vol>>val;
for(int j=vol;j<=V;j++)
c[j]=max(c[j],c[j-vol]+val);
}
cout<<c[V]<<endl;
return 0;
}
/*
in:
4 5
1 2
2 4
3 4
4 5
out:
10
*/
【参考文献】
https://www.bilibili.com/video/BV16F411M7CU
https://www.acwing.com/problem/content/description/3/
https://blog.csdn.net/hnjzsyjyj/article/details/125987923
边栏推荐
猜你喜欢
随机推荐
混动产品谁更吃香,看技术还是看市场?
再谈“雷克萨斯”安全装置失效!安全手册疑点重重,网友:细思极恐
This article understands the process from RS485 sensor to IoT gateway to cloud platform
从餐桌到太空,孙宇晨的“星辰大海”
后台图库上传功能
STM32入门开发 介绍SPI总线、读写W25Q64(FLASH)(硬件+模拟时序)
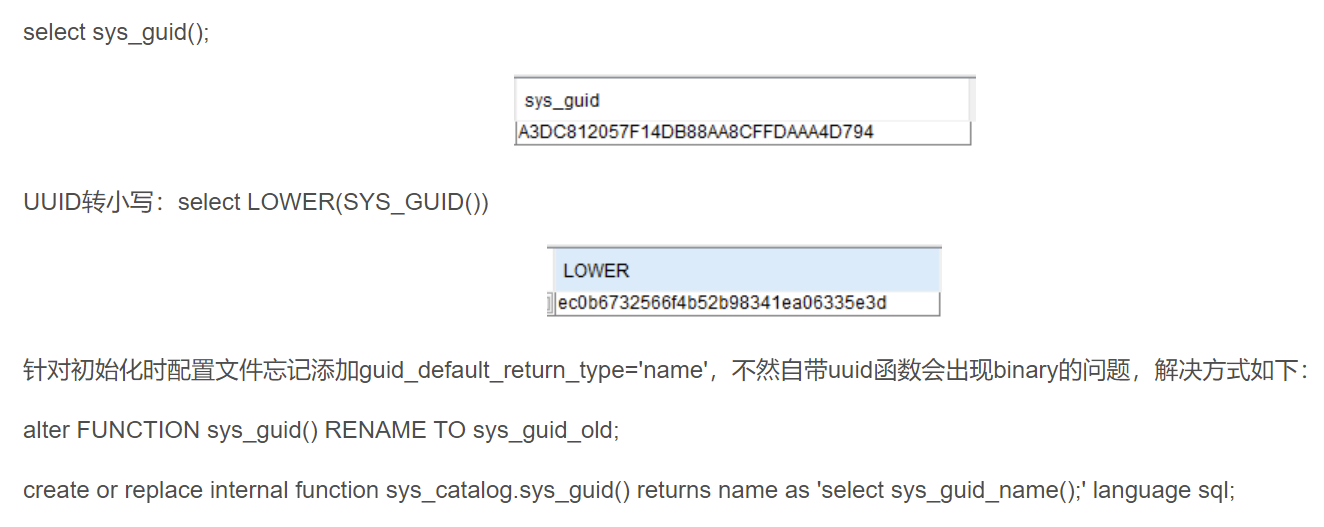
如何改变sys_guid() 返回值类型
记某社区问答
Regulation action for one hundred days during the summer, more than 700 traffic safety hidden dangers were thrown out
分布式事务七种解决方案
OPENCV学习DAY7
多态详细讲解(简单实现买票系统模拟,覆盖/重定义,多态原理,虚表)
面试突击71:GET 和 POST 有什么区别?
Advanced use of MySQL database
error C2872: “flann”: 不明确的符号 解决方法
ARIMA实现(亲测可用)
成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
LeetCode_多叉树_中等_429.N 叉树的层序遍历
免费的mysql数据库管理工具_易语言快速导入MySQL数据库
synchronized