当前位置:网站首页>2022牛客多校第四场C.Easy Counting Problem(EGF+NTT)
2022牛客多校第四场C.Easy Counting Problem(EGF+NTT)
2022-08-05 05:09:00 【吃花椒的妙酱】
题意:给一个字符集,大小不超过10,第i个字符出现次数不少于ci,求字符串长度为n的方案数,至多300个询问,ci<=5000,n<=1e7
(不复制图片了,要钱的比赛不知道会不会被举办==)
思路:指数生成函数
由egf定义,第k个字符的egf为 f ( k ) = ∑ c k + o o x i i ! f(k)=\sum_{c_k}^{+oo}\frac{x^i}{i!} f(k)=∑ck+ooi!xi
则答案为 [ x n n ! ] ∏ k = 1 w f ( k ) , w 为字符集大小 [\frac{x^n}{n!}]\prod_{k=1}^w{f(k)},w为字符集大小 [n!xn]∏k=1wf(k),w为字符集大小
但是n比较大,直接卷肯定不行。改写一下f(k)的形式
f ( k ) = e x p ( x ) − ∑ i = 0 c k − 1 x i i ! f(k)=exp(x)-\sum_{i=0}^{c_k-1}\frac{x^i}{i!} f(k)=exp(x)−∑i=0ck−1i!xi
可以将exp(x)看成一个整体,最后的答案的形式是
∑ i = 0 w g ( i ) ∗ e x p ( x ) i = ∑ i = 0 w g ( i ) ∗ e x p ( i x ) , 其中 g ( i ) 是一个多项式 \sum_{i=0}^wg(i)*exp(x)^i=\sum_{i=0}^wg(i)*exp(ix),其中g(i)是一个多项式 ∑i=0wg(i)∗exp(x)i=∑i=0wg(i)∗exp(ix),其中g(i)是一个多项式
g(i)最高次数不超过 ∑ c i \sum{c_i} ∑ci,而exp(ix)的每项系数都是已知,那么只要遍历每个g(i)项的系数乘上exp(ix)对应项系数即可。最后别忘了乘n!
具体写法可以借鉴dp的思路,设dpij表示前i个f相乘得到的式子exp(jx)的系数是什么,存的是个多项式
转移方程 d p i , j = d p i − 1 , j − d p i , j − 1 ∗ ∑ k = 0 c i − 1 x k k ! dp_{i,j}=dp_{i-1,j} - dp_{i,j-1}*\sum_{k=0}^{c_i-1}\frac{x^k}{k!} dpi,j=dpi−1,j−dpi,j−1∗∑k=0ci−1k!xk,其实就是模拟多项式暴力算罢了,这样思路清楚一点。
复杂度 O ( w 2 s l o g s + q w s ) , s = ∑ c i O(w^2slogs+qws),s=\sum{ci} O(w2slogs+qws),s=∑ci
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(nullptr)
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x7f7f7f7f7f7f7f7f
#define endl "\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
#define ldb long double
const int maxn = 6e6+10;
const int p = 998244353;
const int mod = 998244353;
int Pow(int x,int d){
int tans = 1;
if(d == 0)return 1%p;
int a = Pow(x,d/2);
tans = 1ll*a*a%p;
if(d%2)tans = 1ll*tans*x%p;
return tans%p;
}
typedef vector<int> Poly;//多项式定义
inline Poly operator + (const Poly&A ,const Poly&B){
Poly res (max(A.size(),B.size()),0);
for(int i=0 ;i<max(A.size(),B.size()) ;i++){
if( i < A.size() && i<B.size() ) res[i] = (A[i]+B[i])%mod;
else if( i >= A.size() ){
res[i] = B[i];
}
else res[i] = A[i];
}
return res;
}
inline Poly operator - (const Poly&A ,const Poly&B){
Poly res (max(A.size(),B.size()),0);
for(int i=0 ;i<max(A.size(),B.size()) ;i++){
if( i < A.size() && i<B.size() ) res[i] = (A[i]-B[i]+mod)%mod;
else if( i >= A.size() ){
res[i] = (mod-B[i])%mod;
}
else res[i] = A[i];
}
return res;
}
int F1[maxn],F2[maxn];
int rev[maxn];
void NTT(int * A,int lim,int opt) {
int i, j, k, m, gn, g, tmp;
for(int i = 0; i < lim; ++i)rev[i] = (i & 1)*(lim >> 1) + (rev[i >> 1] >> 1);
for(i = 0; i < lim; ++i)if (rev[i] < i) swap(A[i], A[rev[i]]);
for(m = 2; m <= lim; m <<= 1) {
k = m >> 1;
gn = Pow(3,(p - 1) / m);
for(i = 0; i < lim; i += m) {
g = 1;
for (j = 0; j < k; ++j, g = 1ll * g * gn % p) {
tmp = 1ll * A[i + j + k] * g % p;
A[i + j + k] = (A[i + j] - tmp + p) % p;
A[i + j] = (A[i + j] + tmp) % p;
}
}
}
if(opt == -1){
reverse(A+1,A+lim);
int inv = Pow(lim,p-2);
for(i = 0; i < lim; ++i) A[i] = 1ll * A[i] * inv % p;
}
}
Poly mul(const Poly & A,const Poly & B){
int n = A.size(),m = B.size();
int siz = n + m - 1;
Poly C(siz);
if(siz < 64){
//小于等于64项直接暴力算
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++)C[i+j] = (C[i+j] + 1LL*A[i]*B[j]%p)%p;
}
return C;
}
int fsiz = 1;
while(fsiz <= siz)fsiz *= 2;
for(int i = 0;i < fsiz;i++)F1[i] = F2[i] = 0;
for(int i = 0;i < n;i++)F1[i] = A[i];
for(int i = 0;i < m;i++)F2[i] = B[i];
NTT(F1,fsiz,1);
NTT(F2,fsiz,1);
for(int i = 0;i < fsiz;i++)F1[i] = 1ll*F1[i]*F2[i]%p;
NTT(F1,fsiz,-1);
for(int i = 0;i < siz;i++){
C[i] = F1[i];
}
return C;
}
const int N = 5e5+10;
const int M = 1e7+5;
int W,n;
int c[11],fac[M],ni_f[M];
int mi[11][M];
Poly f[11][11];
ll qsm(int a,int b){
a %= mod;
ll ans=1,tmp=a;
while( b ){
if( b&1 ) ans = (ans * tmp)%mod;
tmp = tmp * tmp%mod;
b>>=1;
}
return ans;
}
void ini(){
int mx = 1e7;
fac[0]=1;
_for(i,1,mx) fac[i] = fac[i-1]*i%mod;
ni_f[mx] = qsm(fac[mx],mod-2);
_rep(i,mx-1,0) ni_f[i] = ni_f[i+1]*(i+1)%mod;
}
int S;
void ff(Poly F){
F.resize(min(S+1,(int)F.size()));
}
void solve(){
f[1][1].resize(1,1);
f[1][0].resize(c[1]+1,0);
_for(i,0,c[1]-1){
f[1][0][i] = (mod-ni_f[i])%mod;
}
_for(i,2,W){
_for(j,0,i){
Poly t (c[i]+1,0);
_for(k,0,c[i]-1){
t[k] = (mod-ni_f[k])%mod;
}
f[i][0] = mul(f[i-1][0],t);
ff(f[i][0]);
f[i][j] = (f[i-1][j-1] + mul(f[i-1][j],t));
ff(f[i][j]);
}
}
}
int Q(int n){
int ans=0;
for(int i=0 ;i<=W ;i++){
// exp(ix)
int pw = qsm(i,n-min(n,(int)f[W][i].size()-1ll));
for(int j=min(n,(int)f[W][i].size()-1ll) ;j>=0 ;j--){
int t = n-j;
if( j < min(n,(int)f[W][i].size()-1ll) ) pw = pw * i%mod;
ans = (ans + f[W][i][j] * pw %mod*ni_f[t]%mod)%mod;
}
}
return ans*fac[n]%mod;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
IOS;
cin>>W;
_for(i,1,W) cin>>c[i];
S = accumulate(c+1,c+1+W,0ll);
ini();
solve();
int q;cin>>q;
while( q-- ){
int x;cin>>x;
int ans = Q(x);
cout<<ans<<endl;
}
AC;
}
边栏推荐
- WPF中DataContext作用
- Using QR codes to solve fixed asset management challenges
- How to deal with DNS hijacking?
- Requests库部署与常用函数讲解
- Flutter真机运行及模拟器运行
- The underlying mechanism of the class
- Flutter学习三-Flutter基本结构和原理
- 【学生毕业设计】基于web学生信息管理系统网站的设计与实现(13个页面)
- Reverse theory knowledge 4
- Cryptography Series: PEM and PKCS7, PKCS8, PKCS12
猜你喜欢
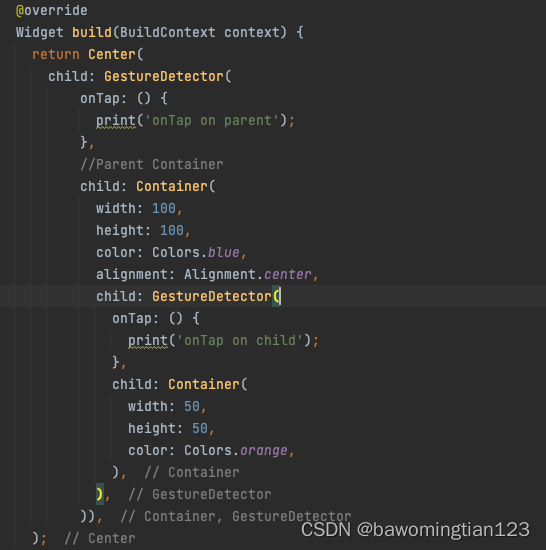
Flutter 父子组件如何都能收到点击事件
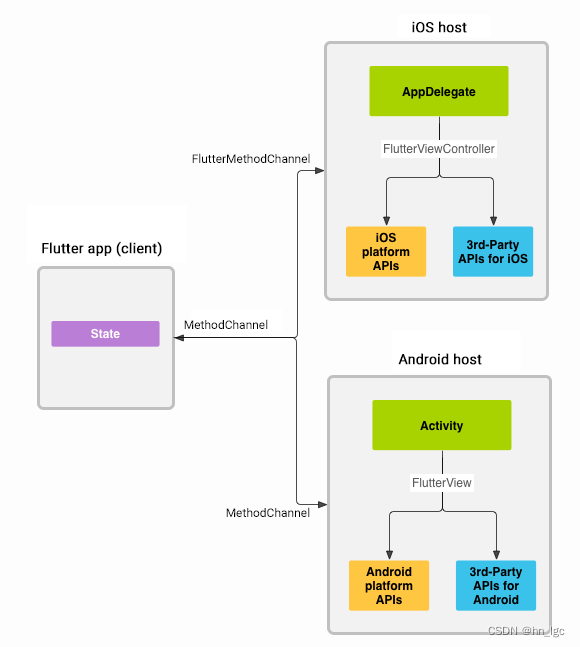
Flutter learning 5-integration-packaging-publish

Analyses the mainstream across technology solutions

span标签和p标签的区别
小程序_动态设置tabBar主题皮肤

Reverse theory knowledge 4
Dephi逆向工具Dede导出函数名MAP导入到IDA中

Application status of digital twin technology in power system

University Physics---Particle Kinematics

使用二维码解决固定资产管理的难题
随机推荐
[Surveying] Quick Summary - Excerpt from Gaoshu Gang
8.04 Day35-----MVC three-tier architecture
LeetCode:1403. 非递增顺序的最小子序列【贪心】
[cesium] element highlighting
In the hot summer, teach you to use Xiaomi smart home accessories + Raspberry Pi 4 to connect to Apple HomeKit
App rapid development and construction experience: the importance of small programs + custom plug-ins
Cryptography Series: PEM and PKCS7, PKCS8, PKCS12
Flutter real machine running and simulator running
Please write the SparkSQL statement
基于Web的商城后台管理系统的设计与实现
AUTOCAD - dimension association
mutillidae download and installation
一篇博客通关Redis技术栈
UVA10827
upload上传图片到腾讯云,如何上传图片
u-boot debugging and positioning means
dedecms error The each() function is deprecated
Flutter Learning 4 - Basic UI Components
for..in和for..of的区别
类的底层机制