当前位置:网站首页>Recommendation system (IX) PNN model (product based neural networks)
Recommendation system (IX) PNN model (product based neural networks)
2022-07-06 04:10:00 【Tianze 28】
Recommendation system ( Nine )PNN Model (Product-based Neural Networks)
Recommendation system series blog :
- Recommendation system ( One ) Overall overview of the recommendation system
- Recommendation system ( Two )GBDT+LR Model
- Recommendation system ( 3、 ... and )Factorization Machines(FM)
- Recommendation system ( Four )Field-aware Factorization Machines(FFM)
- Recommendation system ( 5、 ... and )wide&deep
- Recommendation system ( 6、 ... and )Deep & Cross Network(DCN)
- Recommendation system ( 7、 ... and )xDeepFM Model
- Recommendation system ( 8、 ... and )FNN Model (FM+MLP=FNN)
PNN Model (Product-based Neural Networks) And the last blog introduction FNN The model is the same , They are all from teacher Zhangweinan and his collaborators of Jiaotong University , This article paper Published in ICDM’2016 On , It's a CCF-B Class meeting , Personally, I have never heard of any company in the industry that has practiced this model in its own scenario , But we can still read this paper The results of , Maybe it can provide some reference for your business model . By the name of this model Product-based Neural Networks, We can also basically know PNN By introducing product( It can be inner product or outer product ) To achieve the purpose of feature intersection .
This blog will introduce motivation and model details .
One 、 motivation
This article paper The main improvement is introduced in the last blog FNN,FNN There are two main shortcomings :
- DNN Of embedding Layer quality is limited by FM The quality of training .
- stay FM Implicit vector dot product is used in feature intersection , hold FM Pre trained embedding The vector is sent to MLP Full link layer in ,MLP The full link layer of is essentially a linear weighted sum between features , That is to do 『add』 The operation of , This is related to FM A little inconsistent . in addition ,MLP Different field The difference between , All use linear weighted summation .
The original text of the paper is :
- the quality of embedding initialization is largely limited by the factorization machine.、
- More importantly, the “add” operations of the perceptron layer might not be useful to explore the interactions of categorical data in multiple fields. Previous work [1], [6] has shown that local dependencies between features from different fields can be effectively explored by feature vector “product” operations instead of “add” operations.
Actually, I think FNN There is also a big limitation :FNN It's a two-stage training model , It's not a data-driven Of end-to-end Model ,FNN There is still a strong shadow of traditional machine learning .
Two 、PNN Model details
2.1 PNN The overall structure of the model
PNN The network structure of is shown in the figure below ( The picture is taken from the original paper )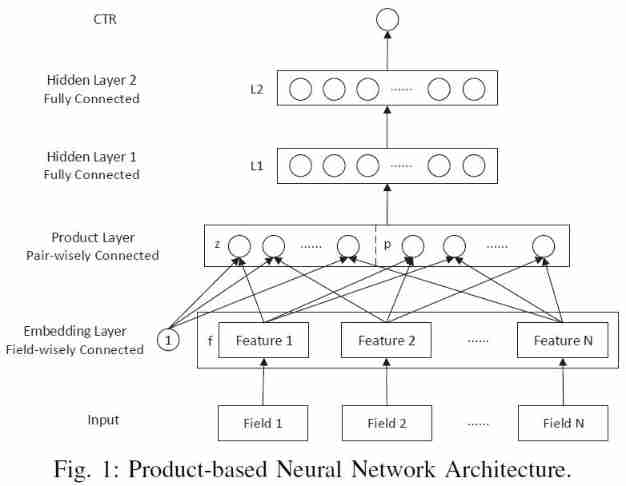
PNN The core of the model is product layer, It's the one in the picture above product layer pair-wisely connected This floor . But unfortunately , The picture given in the original paper hides the most important information , The first impression after reading the above picture is product layer from z z z and p p p form , Then send it directly to the upper L 1 L1 L1 layer . But it's not , What is described in the paper is : z z z and p p p stay product layer The transformation of the whole connection layer is carried out respectively , Separately z z z and p p p The mapping becomes D 1 D_1 D1 Dimension input vector l z l_z lz and l p l_p lp( D 1 D_1 D1 Is the number of neurons in the hidden layer ), And then l z l_z lz and l p l_p lp superposition , Then send it to L 1 L_1 L1 layer .
therefore , I will product layer Redraw , It looks more detailed PNN Model structure , As shown in the figure below :
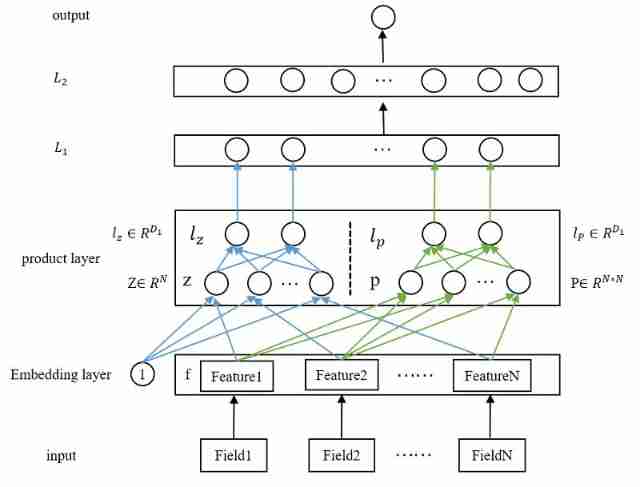
The above figure is basically very clear PNN The overall structure and core details of . Let's take a look at each floor from the bottom up
- Input layer
Original features , There's nothing to say . In the paper is N N N Features . - embedding layer
Nothing to say , Just an ordinary embedding layer , Dimension for D 1 D_1 D1. - product layer
The core of the whole paper , There are two parts here : z z z and p p p, Both are from embedding Layer .
【1. About z z z】
among z z z Is a linear signal vector , In fact, it's just to put N N N Characteristic embedding Vector directly copy To come over , A constant is used in the paper 1, Do multiplication . The paper gives a formal definition :
z = ( z 1 , z 2 , z 3 , . . . , z N ) ≜ ( f 1 , f 2 , f 3 , . . . , f N ) (1) z = (z_1,z_2,z_3,...,z_N) \triangleq (f_1,f_2,f_3,...,f_N) \tag{1} z=(z1,z2,z3,...,zN)≜(f1,f2,f3,...,fN)(1)
among ≜ \triangleq ≜ Is identity , therefore z z z The dimensions are N ∗ M N*M N∗M.
【2. About p p p】
p p p Here is the real cross operation , About how to generate p p p, The paper gives a formal definition : p i , j = g ( f i , f j ) p_{i,j}=g(f_i,f_j) pi,j=g(fi,fj), there g g g Theoretically, it can be any mapping function , This paper gives two kinds of mappings : The inner product and the outer product , Corresponding to IPNN and OPNN. therefore :
p = { p i , j } , i = 1 , 2 , . . . , N ; j = 1 , 2 , . . . , N (2) p=\{p_{i,j}\}, i=1,2,...,N;j=1,2,...,N \tag{2} p={ pi,j},i=1,2,...,N;j=1,2,...,N(2)
therefore , p p p The dimensions are N 2 ∗ M N^2*M N2∗M.
【3. About l z l_z lz】
With z z z after , Through a fully connected network , Such as in the figure above product layer in The blue line part , Finally mapped to D 1 D_1 D1 dimension ( Number of hidden layer units ) Vector , The formal expression is :
l z = ( l z 1 , l z 2 , . . . , l z k , . . . , l z D 1 ) l z k = W z k ⊙ z (3) l_z=(l_z^1,l_z^2,...,l_z^k,...,l_z^{D_1}) \ \ \ \ \ \ \ \ \ \ \ \ l_z^k=W_z^k\odot z \tag{3} lz=(lz1,lz2,...,lzk,...,lzD1) lzk=Wzk⊙z(3)
among , ⊙ \odot ⊙ Is the inner product symbol , Defined as : A ⊙ B ≜ ∑ i , j A i j A i j A\odot B\triangleq \sum_{i,j}A_{ij}A_{ij} A⊙B≜∑i,jAijAij, because z z z The dimensions are N ∗ M N*M N∗M, therefore W z k W_z^k Wzk The dimension of is also N ∗ M N*M N∗M.
【4. About l p l_p lp】
and l z l_z lz equally , Through a fully connected network , Such as in the figure above product layer in The green line , Finally mapped to D 1 D_1 D1 dimension ( Number of hidden layer units ) Vector , The formal expression is :
l p = ( l p 1 , l p 2 , . . . , l p k , . . . , l z D 1 ) l z k = W p k ⊙ p (4) l_p=(l_p^1,l_p^2,...,l_p^k,...,l_z^{D_1}) \ \ \ \ \ \ \ \ \ \ \ \ l_z^k=W_p^k\odot p \tag{4} lp=(lp1,lp2,...,lpk,...,lzD1) lzk=Wpk⊙p(4)
W p k W_p^k Wpk And p p p The dimensions of are the same , by N 2 ∗ M N^2*M N2∗M. - Fully connected layer
Here is the ordinary two-layer full connection layer , Go straight to the formula , Simple and clear .
l 1 = r e l u ( l z + l p + b 1 ) (5) l_1 = relu(l_z + l_p + b_1) \tag{5} l1=relu(lz+lp+b1)(5)
l 2 = r e l u ( W 2 l 1 + b 2 ) (6) l_2 = relu(W_2l_1 + b_2) \tag{6} l2=relu(W2l1+b2)(6) - Output layer
Because the scene is CTR forecast , So it is classified into two categories , Activate the function directly sigmoid,
y ^ = σ ( W 3 l 2 + b 3 ) (6) \hat{y} = \sigma(W_3l_2 + b_3) \tag{6} y^=σ(W3l2+b3)(6) - Loss function
Cross entropy goes ,
L ( y , y ^ ) = − y log y ^ − ( 1 − y ) log ( 1 − y ) ^ (7) L(y,\hat{y}) = -y\log\hat{y} - (1-y)\log\hat{(1-y)} \tag{7} L(y,y^)=−ylogy^−(1−y)log(1−y)^(7)
2.2 IPNN
stay product layer , On features embedding Vectors do cross , Theoretically, it can be any operation , This article paper Two ways are given : The inner product and the outer product , They correspond to each other IPNN and OPNN. In terms of complexity ,IPNN The complexity is lower than OPNN, Therefore, if you plan to implement the industry , Don't think about OPNN 了 , So I will introduce it in detail IPNN.
IPNN, That is to say product Layers do inner product operation , According to the definition of inner product given above , It can be seen that the result of the inner product of two vectors is a scalar . The formal expression is :
g ( f i , f j ) = < f i , f j > (8) g(f_i,f_j) = <f_i,f_j> \tag{8} g(fi,fj)=<fi,fj>(8)
Let's analyze IPNN Time complexity of , In defining the dimensions of the next few variables :embedding Dimension for M M M, The number of features is N N N, l p l_p lp and l z l_z lz The dimensions are D 1 D_1 D1. Because we need to cross the features in pairs , therefore p p p The size is N ∗ N N*N N∗N, So get p p p The time complexity of is N ∗ N ∗ M N*N*M N∗N∗M, With p p p, After mapping, we get l p l_p lp The time complexity of is N ∗ N ∗ D 1 N*N*D_1 N∗N∗D1, So for IPNN, Whole product The time complexity of the layer is O ( N ∗ N ( D 1 + M ) ) O(N*N(D1+M)) O(N∗N(D1+M)), This time complexity is very high , So it needs to be optimized , The technique of matrix decomposition is used in this paper , Reduce the time complexity to D 1 ∗ M ∗ N D1*M*N D1∗M∗N. Let's see how the paper is done :
Because the features intersect , therefore p p p It's obviously a N ∗ N N*N N∗N The symmetric matrix of , be W p k W_p^k Wpk It's also a N ∗ N N*N N∗N The symmetric matrix of , obviously W p k W_p^k Wpk It can be decomposed into two N N N Multiplied by dimensional vectors , hypothesis W p k = θ k ( θ k ) T W_p^k=\theta^k(\theta^k)^T Wpk=θk(θk)T, among θ k ∈ R N \theta^k\in R^N θk∈RN.
therefore , We have :
W p k ⊙ p = ∑ i = 1 N ∑ j = 1 N θ i k θ j k < f i , f j > = < ∑ i = 1 N θ i k f i , ∑ j = 1 N θ j k f j > (9) W_p^k \odot p = \sum_{i=1}^N\sum_{j=1}^N\theta^k_i\theta^k_j<f_i,f_j> = <\sum_{i=1}^N\theta^k_if_i, \sum_{j=1}^N\theta^k_jf_j> \tag{9} Wpk⊙p=i=1∑Nj=1∑Nθikθjk<fi,fj>=<i=1∑Nθikfi,j=1∑Nθjkfj>(9)
If we remember δ i k = θ i k f i \delta_i^k=\theta^k_if_i δik=θikfi, be δ i k ∈ R M \delta_i^k \in R^M δik∈RM, δ i k = ( δ 1 k , δ 2 k , . . . , δ N k ) ∈ R N ∗ M \delta_i^k=(\delta_1^k,\delta_2^k,...,\delta_N^k) \in R^{N*M} δik=(δ1k,δ2k,...,δNk)∈RN∗M.
therefore l p l_p lp by :
l p = ( ∣ ∣ ∑ i δ i 1 ∣ ∣ , . . . . , ∣ ∣ ∑ i δ i D 1 ∣ ∣ ) (10) l_p = (||\sum_i\delta_i^1||,....,||\sum_i\delta_i^{D_{1}}||) \tag{10} lp=(∣∣i∑δi1∣∣,....,∣∣i∑δiD1∣∣)(10)
The above series of formulas go up , It is estimated that there are not enough people interested in reading this blog 10% 了 , It's too obscure to understand . Want others to understand , The simplest way is to give examples , Let's go straight to the example , Suppose our sample has 3 Features , Every feature of embedding Dimension for 2, namely N = 3 , M = 2 N=3, M=2 N=3,M=2, So we have the following sample :
| features (field) | embedding vector |
|---|---|
| f 1 f_1 f1 | [1,2] |
| f 2 f_2 f2 | [3,4] |
| f 1 f_1 f1 | [5,6] |
It is represented by a matrix as :
[ 1 2 3 4 5 6 ] (11) \begin{bmatrix} 1& 2 \\ 3&4 \\ 5&6 \\ \end{bmatrix} \tag{11} ⎣⎡135246⎦⎤(11)
Then define W p 1 W_p^1 Wp1:
W p 1 = [ 1 2 3 2 4 6 3 6 9 ] (12) W_p^1 = \begin{bmatrix} 1& 2 & 3\\ 2&4 & 6\\ 3&6 &9 \\ \end{bmatrix} \tag{12} Wp1=⎣⎡123246369⎦⎤(12)
Let's separate them according to the ( The complexity is O ( N ∗ N ( D 1 + M ) ) O(N*N(D1+M)) O(N∗N(D1+M))) And decomposition, then calculate , As soon as we compare, we find the mystery .
- Before decomposition
Direct pair ( f 1 , f 2 , f 3 ) (f_1,f_2,f_3) (f1,f2,f3) Do the inner product in pairs to get the matrix p p p, The calculation process is as follows :
p = [ 1 2 3 4 5 6 ] ⋅ [ 1 3 5 2 4 6 ] = [ 5 11 17 11 25 39 17 39 61 ] (13) p = \begin{bmatrix} 1& 2 \\ 3&4 \\ 5&6 \\ \end{bmatrix} \cdot \begin{bmatrix} 1& 3 & 5 \\ 2&4 & 6 \\ \end{bmatrix} = \begin{bmatrix} 5& 11 & 17 \\ 11& 25 & 39 \\ 17& 39 & 61 \\ \end{bmatrix} \tag{13} p=⎣⎡135246⎦⎤⋅[123456]=⎣⎡51117112539173961⎦⎤(13)
among p i j = f i ⊙ f j p_{ij} = f_i \odot f_j pij=fi⊙fj.
With p p p, Let's calculate l p 1 l_p^1 lp1, In fact, it is an arithmetic 2 in product Layer l p l_p lp( The green part ) The value of the first element of , Yes :
W p 1 ⊙ p = [ 1 2 3 2 4 6 3 6 9 ] ⊙ [ 5 11 17 11 25 39 17 39 61 ] = s u m ( [ 5 22 51 22 100 234 51 234 549 ] ) = 1268 (14) W_p^1 \odot p = \begin{bmatrix} 1& 2 & 3\\ 2&4 & 6\\ 3&6 &9 \\ \end{bmatrix} \odot \begin{bmatrix} 5& 11 & 17 \\ 11& 25 & 39 \\ 17& 39 & 61 \\ \end{bmatrix} = sum(\begin{bmatrix} 5 &22 & 51 \\ 22 &100 &234 \\ 51 &234 &549 \\ \end{bmatrix}) = 1268 \tag{14} Wp1⊙p=⎣⎡123246369⎦⎤⊙⎣⎡51117112539173961⎦⎤=sum(⎣⎡522512210023451234549⎦⎤)=1268(14) - After decomposition
W p 1 W_p^1 Wp1 Obviously, it can be decomposed , Can be broken down into :
W p 1 = [ 1 2 3 2 4 6 3 6 9 ] = [ 1 2 3 ] [ 1 2 3 ] = θ 1 ( θ 1 ) T (15) W_p^1 = \begin{bmatrix} 1& 2 & 3\\ 2&4 & 6\\ 3&6 &9 \\ \end{bmatrix} = \begin{bmatrix} 1\\ 2\\ 3 \\ \end{bmatrix} \begin{bmatrix} 1&2&3\\ \end{bmatrix} = \theta^1 (\theta^1)^T \tag{15} Wp1=⎣⎡123246369⎦⎤=⎣⎡123⎦⎤[123]=θ1(θ1)T(15)
So according to the formula δ i 1 = θ i 1 f i \delta_i^1=\theta^1_if_i δi1=θi1fi, So let's calculate δ i 1 \delta_i^1 δi1, See the table below :
| features (field) | embedding vector | θ i 1 \theta^1_i θi1 | δ i 1 \delta_i^1 δi1 |
|---|---|---|---|
| f 1 f_1 f1 | [1,2] | 1 | [1,2] |
| f 2 f_2 f2 | [3,4] | 2 | [6,8] |
| f 1 f_1 f1 | [5,6] | 3 | [15,18] |
Because there is still a step to be done ∑ i = 1 N δ i 1 \sum_{i=1}^N\delta_i^1 ∑i=1Nδi1, therefore , Finally, we get the vector δ 1 \delta^1 δ1:
δ 1 = ∑ i = 1 N δ i 1 = [ 22 28 ] (16) \delta^1 = \sum_{i=1}^N\delta_i^1 = \begin{bmatrix} 22& 28 \end{bmatrix} \tag{16} δ1=i=1∑Nδi1=[2228](16)
So in the end :
< δ 1 , δ 1 > = δ 1 ⊙ δ 1 = [ 22 28 ] ⊙ [ 22 28 ] = 1268 (17) <\delta^1, \delta^1> = \delta^1 \odot \delta^1 = \begin{bmatrix} \tag{17} 22& 28 \end{bmatrix} \odot \begin{bmatrix} 22& 28 \end{bmatrix} = 1268 <δ1,δ1>=δ1⊙δ1=[2228]⊙[2228]=1268(17)
therefore , Finally we can find , Calculated before and after decomposition l p l_p lp The value of the first element of is the same , The time complexity after decomposition is only O ( D 1 ∗ M ∗ N ) O(D1*M*N) O(D1∗M∗N).
therefore , We are realizing IPNN When , The dimension of parameter matrix of linear part and cross part is :
- For linear weight matrix W z W_z Wz Come on , The size is D 1 ∗ N ∗ M D_1 * N * M D1∗N∗M.
- Pair crossover ( square ) Weight matrices W p W_p Wp Come on , The size is D 1 ∗ N D_1 * N D1∗N.
2.3 OPNN
OPNN and IPNN The only difference is that product layer Middle computation l p l_p lp From inner product to outer product , As a result of the outer product operation, we get a M ∗ M M*M M∗M Matrix , namely :
g ( f i , f j ) = f i f j T (18) g(f_i,f_j) = f_if_j^T \tag{18} g(fi,fj)=fifjT(18)
therefore ,OPNN The whole time is complicated as O ( D 1 M 2 N 2 ) O(D1M^2N^2) O(D1M2N2), The time complexity is also high , therefore , In this paper, a superposition (superposition) Methods , To reduce time complexity , Let's take a look at the formula :
p = ∑ i = 1 N ∑ j = 1 N f i f j T = f ∑ ( f ∑ ) T (19) p = \sum_{i=1}^N \sum_{j=1}^N f_i f_j^T = f_{\sum}(f_{\sum})^T \tag{19} p=i=1∑Nj=1∑NfifjT=f∑(f∑)T(19)
among , f ∑ = ∑ i = 1 N f i f_{\sum} = \sum_{i=1}^Nf_i f∑=∑i=1Nfi .
After the above simplification ,OPNN The time complexity is reduced to O ( D 1 M ( M + N ) ) O(D1M(M + N)) O(D1M(M+N)).
But let's look at the above formula (19), f ∑ = ∑ i = 1 N f i f_{\sum} = \sum_{i=1}^Nf_i f∑=∑i=1Nfi, This is equivalent to making an analysis of all features sum pooling, That is to add the corresponding dimension elements of different features , There may be some problems in the actual business , For example, two features : Age and gender , These two characteristics embedding Vectors are not in a vector space , Do this forcibly sum pooling May cause some unexpected problems . We pass only for multivalued features , For example, the user clicks in history item Of embedding Vector do pooling, There's no problem with that , because item Ben is in the same vector space , And it has practical significance .
In practice , I suggest to use IPNN.
reference
[1]: Yanru Qu et al. Product-Based Neural Networks for User Response Prediction. ICDM 2016: 1149-1154
边栏推荐
- Scalpel like analysis of JVM -- this article takes you to peek into the secrets of JVM
- Take you to wechat applet development in 3 minutes
- Stc8h development (XII): I2C drive AT24C08, at24c32 series EEPROM storage
- Leetcode32 longest valid bracket (dynamic programming difficult problem)
- Query the number and size of records in each table in MySQL database
- 【PSO】基于PSO粒子群优化的物料点货物运输成本最低值计算matlab仿真,包括运输费用、代理人转换费用、运输方式转化费用和时间惩罚费用
- Determine which week of the month the day is
- C mouse event and keyboard event of C (XXVIII)
- MySQL transaction isolation level
- 查询mysql数据库中各表记录数大小
猜你喜欢
Error 1045 (28000): access denied for user 'root' @ 'localhost' (using password: no/yes

Facebook等大廠超十億用戶數據遭泄露,早該關注DID了

C mouse event and keyboard event of C (XXVIII)
![[disassembly] a visual air fryer. By the way, analyze the internal circuit](/img/73/29553d60f47deadfff420be40b7f77.jpg)
[disassembly] a visual air fryer. By the way, analyze the internal circuit
Detailed explanation of serialization and deserialization

MySQL master-slave replication
![[FPGA tutorial case 11] design and implementation of divider based on vivado core](/img/39/f337510c2647d365603a8485583a20.png)
[FPGA tutorial case 11] design and implementation of divider based on vivado core

Scalpel like analysis of JVM -- this article takes you to peek into the secrets of JVM
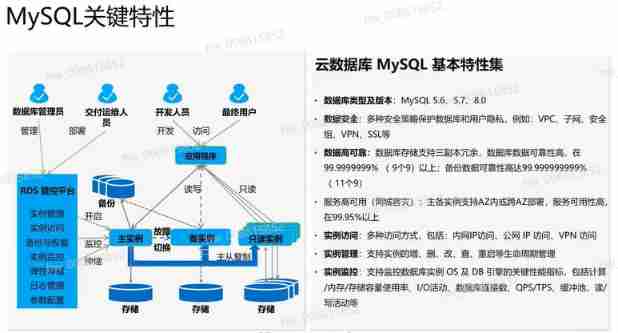
Stable Huawei micro certification, stable Huawei cloud database service practice
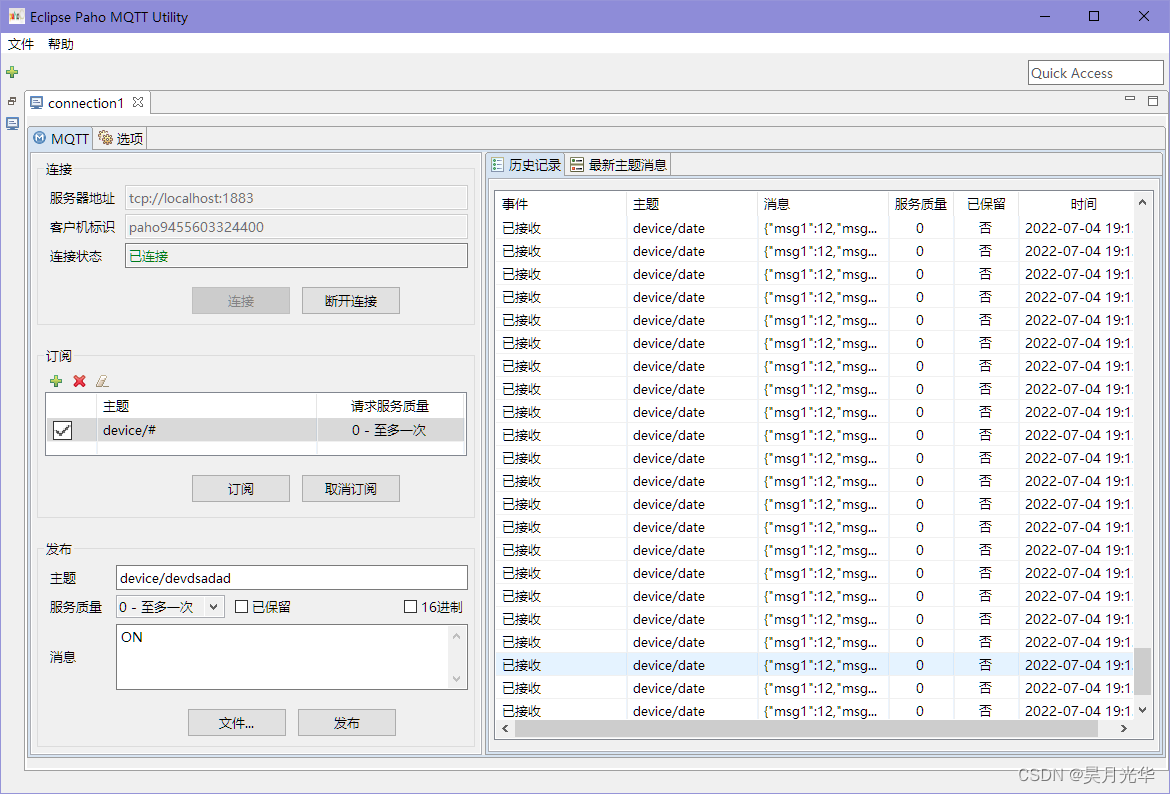
ESP32(基于Arduino)连接EMQX的Mqtt服务器上传信息与命令控制
随机推荐
Global and Chinese markets for endoscopic drying storage cabinets 2022-2028: Research Report on technology, participants, trends, market size and share
Mlapi series - 04 - network variables and network serialization [network synchronization]
Stc8h development (XII): I2C drive AT24C08, at24c32 series EEPROM storage
DM8 archive log file manual switching
[001] [stm32] how to download STM32 original factory data
Chinese brand hybrid technology: there is no best technical route, only better products
C mouse event and keyboard event of C (XXVIII)
C (XXIX) C listbox CheckedListBox Imagelist
C form application of C (27)
MySQL transaction isolation level
关于进程、线程、协程、同步、异步、阻塞、非阻塞、并发、并行、串行的理解
Introduction to data types in MySQL
Proof of Stirling formula
In Net 6 CS more concise method
P3033 [usaco11nov]cow steelchase g (similar to minimum path coverage)
Simple blog system
Execution order of scripts bound to game objects
10個 Istio 流量管理 最常用的例子,你知道幾個?
mysql关于自增长增长问题
C (thirty) C combobox listview TreeView