当前位置:网站首页>P7735-[noi2021] heavy and heavy edges [tree chain dissection, line segment tree]
P7735-[noi2021] heavy and heavy edges [tree chain dissection, line segment tree]
2022-07-06 03:44:00 【QuantAsk】
Preface
On the front line of A I'm writing a blog now 
On the subject
Topic link :https://www.luogu.com.cn/problem/P7735
The main idea of the topic
Yes n n n A tree at a point , All edges are light at first , m m m operations .
- hold x → y x\rightarrow y x→y The heavy edges connected by all points on the path become light edges , Then turn the edge on the path into a heavy edge .
- Ask the number of heavy edges on a path .
1 ≤ T ≤ 3 , 1 ≤ n , m ≤ 1 0 5 1\leq T\leq 3,1\leq n,m\leq 10^5 1≤T≤3,1≤n,m≤105
Their thinking
Just find a spot to be the root , We use each point to store the information it connects to its parent node .
Then consider how to operate , Discovery is a path operation on the tree , Consider tree chain subdivision .
* For the convenience of description, we use the light and heavy sides of tree chain partition In bold Describe
First, we can put all the edges on the path ( Information stored at the corresponding point ) Change to double edge , Then the problem lies in how to change the heavy edge of the connection into a light edge .
It is obviously not feasible to modify these edges violently , We notice that we can easily modify the tree chain after splitting Heavy edge , And on a path Light side Not many paths , So we can consider maintaining only the important edge information , We can process the light edge information when we query .
Then it's obvious , about Heavy edge We use the segment tree to modify the information of , And for Light side , We open a segment tree to record the path number of each endpoint covered last time .
If Light side The two endpoints connected are covered by different paths , Then this side is the light side , Otherwise, it is the heavy side .
Time complexity : O ( m log 2 n ) O(m\log^2 n) O(mlog2n)
code
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cctype>
using namespace std;
const int N=1e5+10;
int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){
if(c=='-')f=-f;c=getchar();}
while(isdigit(c)){
x=(x<<1)+(x<<3)+c-48;c=getchar();}
return x*f;
}
struct node{
int to,next;
}a[N<<1];
int T,n,m,cnt,tot,ls[N],fa[N],dep[N];
int rfn[N],ed[N],siz[N],son[N],top[N],id[N];
void addl(int x,int y){
a[++tot].to=y;
a[tot].next=ls[x];
ls[x]=tot;return;
}
void dfs(int x){
rfn[x]=++cnt;siz[x]=1;
dep[x]=dep[fa[x]]+1;
for(int i=ls[x];i;i=a[i].next){
int y=a[i].to;
if(y==fa[x])continue;
fa[y]=x;dfs(y);
siz[x]+=siz[y];
if(siz[y]>siz[son[x]])son[x]=y;
}
ed[x]=cnt;
return;
}
void dFs(int x){
id[x]=++cnt;
if(son[x]){
top[son[x]]=top[x];
dFs(son[x]);
}
for(int i=ls[x];i;i=a[i].next){
int y=a[i].to;
if(y==fa[x]||y==son[x])continue;
top[y]=y;dFs(y);
}
return;
}
struct SegTree{
int w[N<<2],lazy[N<<2];
void Clear(){
memset(w,0,sizeof(w));
memset(lazy,0,sizeof(lazy));
return;
}
void Downdata(int x,int l,int r){
if(!lazy[x])return;int mid=(l+r)>>1;
w[x*2]=(mid-l+1)*lazy[x];
w[x*2+1]=(r-mid)*lazy[x];
lazy[x*2]=lazy[x*2+1]=lazy[x];
lazy[x]=0;return;
}
int Ask(int x,int L,int R,int l,int r){
if(L==l&&R==r)return w[x];
int mid=(L+R)>>1;Downdata(x,L,R);
if(r<=mid)return Ask(x*2,L,mid,l,r);
if(l>mid)return Ask(x*2+1,mid+1,R,l,r);
return Ask(x*2,L,mid,l,mid)+Ask(x*2+1,mid+1,R,mid+1,r);
}
void Change(int x,int L,int R,int l,int r,int val){
if(L==l&&R==r){
w[x]=(R-L+1)*val;lazy[x]=val;return;}
int mid=(L+R)>>1;Downdata(x,L,R);
if(r<=mid)Change(x*2,L,mid,l,r,val);
else if(l>mid)Change(x*2+1,mid+1,R,l,r,val);
else Change(x*2,L,mid,l,mid,val),Change(x*2+1,mid+1,R,mid+1,r,val);
w[x]=w[x*2]+w[x*2+1];
}
}Tw,Tl;
void Updata(int x,int y,int pos){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
if(top[x]!=x)Tw.Change(1,1,n,id[top[x]]+1,id[x],1);
Tl.Change(1,1,n,id[top[x]],id[x],pos);
if(son[x])Tw.Change(1,1,n,id[x]+1,id[x]+1,0);
x=fa[top[x]];
}
if(dep[x]>dep[y])swap(x,y);
Tl.Change(1,1,n,id[x],id[y],pos);
if(id[x]!=id[y])Tw.Change(1,1,n,id[x]+1,id[y],1);
if(son[y])Tw.Change(1,1,n,id[y]+1,id[y]+1,0);
if(top[x]!=x)Tw.Change(1,1,n,id[x],id[x],0);
}
bool check(int x){
int p=Tl.Ask(1,1,n,id[x],id[x]);
if(!p)return 0;
return (p==Tl.Ask(1,1,n,id[fa[x]],id[fa[x]]));
}
int Ask(int x,int y){
int ans=0;
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
ans+=Tw.Ask(1,1,n,id[top[x]],id[x]);
x=top[x];ans+=check(x);
x=fa[x];
}
if(dep[x]>dep[y])swap(x,y);
if(id[x]!=id[y])ans+=Tw.Ask(1,1,n,id[x]+1,id[y]);
return ans;
}
int main()
{
T=read();
while(T--){
tot=0;
memset(ls,0,sizeof(ls));
memset(fa,0,sizeof(fa));
memset(son,0,sizeof(son));
Tl.Clear();Tw.Clear();
n=read();m=read();
for(int i=1;i<n;i++){
int x=read(),y=read();
addl(x,y);addl(y,x);
}
cnt=0;dfs(1);cnt=0;
top[1]=1;dFs(1);cnt=0;
while(m--){
int op=read(),x=read(),y=read();
if(op==1)++cnt,Updata(x,y,cnt);
else cout<<Ask(x,y)<<'\n';
}
}
return 0;
}
边栏推荐
- Failure causes and optimization methods of LTE CSFB
- C#(二十九)之C#listBox checkedlistbox imagelist
- Python implementation of maddpg - (1) openai maddpg environment configuration
- 简易博客系统
- Factors affecting user perception
- Recommended papers on remote sensing image super-resolution
- Computer graduation project asp Net fitness management system VS development SQLSERVER database web structure c programming computer web page source code project
- 在 .NET 6 中使用 Startup.cs 更简洁的方法
- C#(三十一)之自定义事件
- Restful style
猜你喜欢
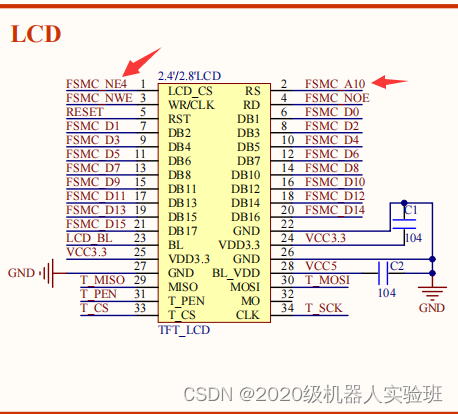
Cubemx transplantation punctual atom LCD display routine
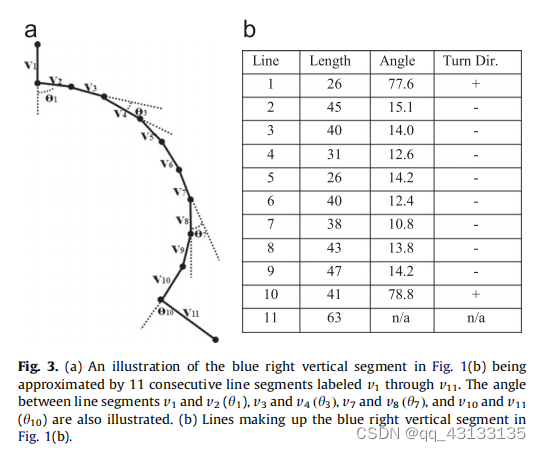
EDCircles: A real-time circle detector with a false detection control 翻译

C#(三十)之C#comboBox ListView treeView
![[risc-v] external interrupt](/img/9d/eb1c27e14045d9f1f690f4a7f5c596.jpg)
[risc-v] external interrupt
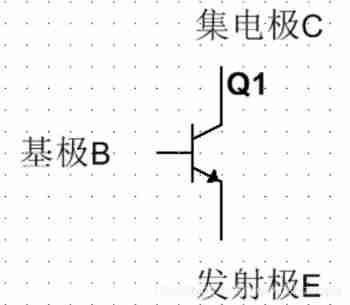
Ethernet port &arm & MOS &push-pull open drain &up and down &high and low sides &time domain and frequency domain Fourier
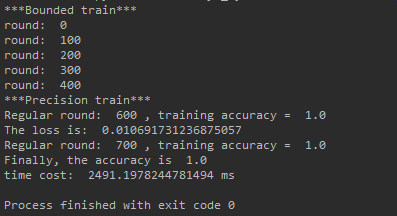
Teach you to build your own simple BP neural network with pytoch (take iris data set as an example)
![[slam] orb-slam3 parsing - track () (3)](/img/87/b580837778c2c9f6bac5ba49403d6b.png)
[slam] orb-slam3 parsing - track () (3)
Python implementation of maddpg - (1) openai maddpg environment configuration
![[analysis of variance] single factor analysis and multi factor analysis](/img/92/5337d0ef6e487d1af2f56cb3a3268a.jpg)
[analysis of variance] single factor analysis and multi factor analysis
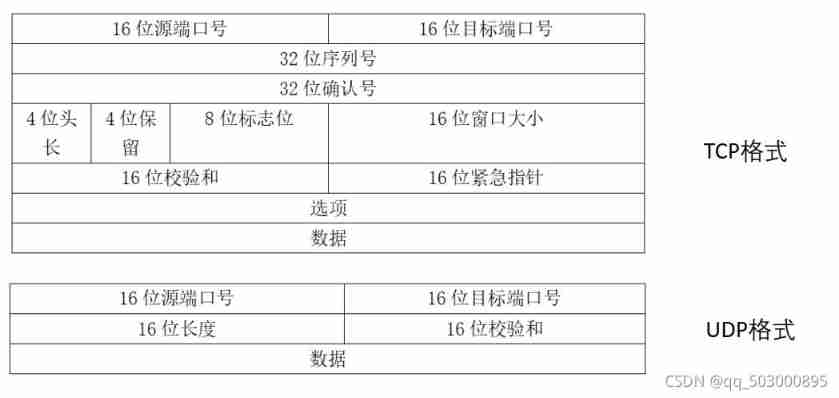
UDP reliable transport protocol (quic)
随机推荐
Pytorch load data
Cubemx transplantation punctual atom LCD display routine
在 .NET 6 中使用 Startup.cs 更简洁的方法
Pytorch基础——(2)张量(tensor)的数学运算
cookie,session,Token 这些你都知道吗?
[risc-v] external interrupt
3.2 detailed explanation of rtthread serial port device (V2)
Restful style
Idea push rejected solution
C#(二十八)之C#鼠标事件、键盘事件
Image super resolution using deep revolutionary networks (srcnn) interpretation and Implementation
Pointer written test questions ~ approaching Dachang
Getting started with applet cloud development - getting user search content
2.2 fonctionnement stm32 GPIO
[slam] orb-slam3 parsing - track () (3)
Python implementation of maddpg - (1) openai maddpg environment configuration
2.1 rtthread pin device details
WPF效果第一百九十一篇之框选ListBox
Canvas cut blocks game code
Overview of super-resolution reconstruction of remote sensing images