当前位置:网站首页>CCPC 2021 Weihai - G. shinyruo and KFC (combination number, tips)
CCPC 2021 Weihai - G. shinyruo and KFC (combination number, tips)
2022-07-05 20:23:00 【Dimple】
G. Shinyruo and KFC
The question
Altogether n n n Kind of food , Each food has a i a_i ai individual . The total number of food should not exceed 1 0 5 10^5 105.
Now I want to share these foods with k k k personal , Everyone can take many things , But each kind of food takes at most 1 individual .
about k k k from 1 To m m m, Output the food distribution plan separately .
Answer model 998244353 998244353 998244353.
1 ≤ m , n ≤ 5 ⋅ 1 0 4 1 \le m,n \le 5 \cdot 10^4 1≤m,n≤5⋅104
0 ≤ a i ≤ 1 0 5 , ∑ i = 1 n a i ≤ 1 0 5 0\le a_i\le 10^5,\ \sum_{i=1}^n a_i\le 10^5 0≤ai≤105, ∑i=1nai≤105
Ideas
Common to one food a i a_i ai individual , among k k k personal , Each person can get one at most , Then the distribution scheme is C ( k , a i ) C(k, ai) C(k,ai).
that n Kind of food , among k The overall personal distribution plan is : ∏ i = 1 n C ( k , a i ) \prod_{i=1}^{n} C(k, a_i) ∏i=1nC(k,ai);
Re traversal m personal , In this case, the minimum time complexity is O(n * m), Overtime .
And the title says ai The total does not exceed 1e5, that ai The number of species is 1 e 5 \sqrt {1e5} 1e5 Level , For repetition, use fast power to find power .
Preprocess the inverse element to find the combination number .
In this way, the time complexity is reduced to : O ( m n l o g n ) O(m \sqrt n \ logn) O(mn logn)
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define fi first
#define se second
#define endl '\n'
map<int,int> mp;
const int N = 200010, mod = 998244353;
int T, n, m;
int a[N];
struct node{
int x, cnt;
}b[N];
int fac[N], inv[N], finv[N];
int qmi(int x, int y)
{
int ans = 1;
while(y)
{
if(y & 1) ans = ans * x % mod;
x = x*x % mod;
y >>= 1;
}
return ans;
}
void init(){
fac[0]=inv[0]=inv[1]=finv[0]=finv[1]=1ll;
for(int i=1;i<N;i++)fac[i]=fac[i-1]*i%mod;
for(int i=2;i<N;i++)inv[i]=(mod-mod/i)*inv[mod%i]%mod;
for(int i=2;i<N;i++)finv[i]=finv[i-1]*inv[i]%mod;
}
inline int C(int a,int b){
if(b>a)return 0;
else return fac[a]*finv[a-b]%mod*finv[b]%mod;
}
signed main(){
Ios;
cin >> n >> m;
for(int i=1;i<=n;i++) cin >> a[i], mp[a[i]]++;
int cnt = 0;
for(auto it : mp)
{
cnt++;
b[cnt] = {
it.first, it.second};
}
init();
for(int i=1;i<=m;i++)
{
int ans = 1;
for(int j=1;j<=cnt;j++)
{
ans = ans * qmi(C(i, b[j].x), b[j].cnt) % mod;
}
cout << ans << endl;
}
return 0;
}
Experience
- If n The sum of the numbers does not exceed m, Then the number of types of these numbers is m \sqrt m m Level .
边栏推荐
- [C language] merge sort
- Practical demonstration: how can the production research team efficiently build the requirements workflow?
- Leetcode(695)——岛屿的最大面积
- Fundamentals - configuration file analysis
- Guidelines for application of Shenzhen green and low carbon industry support plan in 2023
- model方法
- Leetcode brush questions: binary tree 11 (balanced binary tree)
- Rainbow 5.7.1 supports docking with multiple public clouds and clusters for abnormal alarms
- y57.第三章 Kubernetes从入门到精通 -- 业务镜像版本升级及回滚(三十)
- mongodb基操的练习
猜你喜欢
基础篇——配置文件解析

14、Transformer--VIT TNT BETR
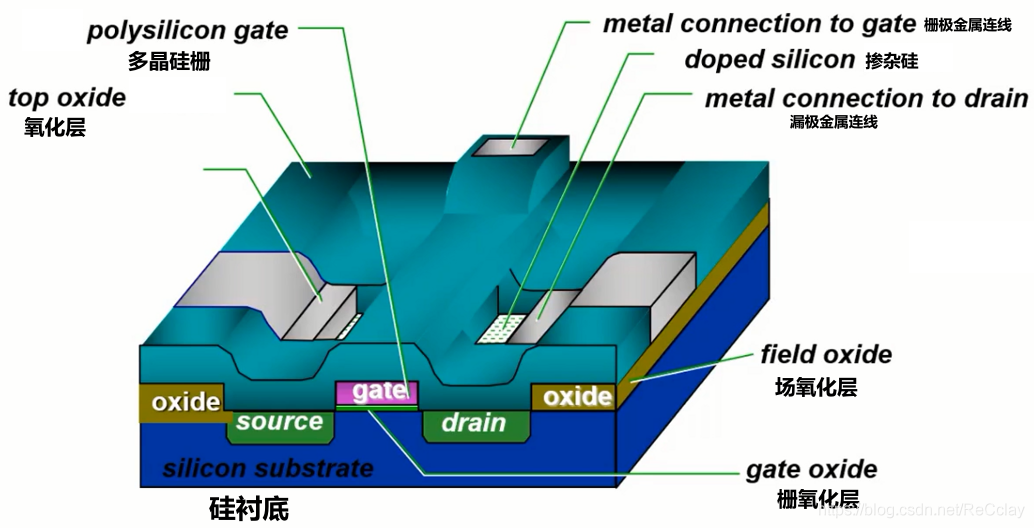
【数字IC验证快速入门】7、验证岗位中必备的数字电路基础知识(含常见面试题)
Go language | 01 wsl+vscode environment construction pit avoidance Guide
Rainbow 5.7.1 supports docking with multiple public clouds and clusters for abnormal alarms
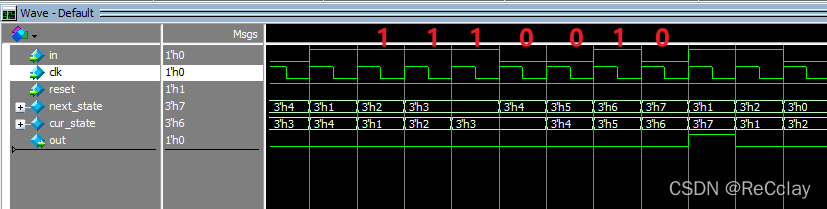
【数字IC验证快速入门】9、Verilog RTL设计必会的有限状态机(FSM)
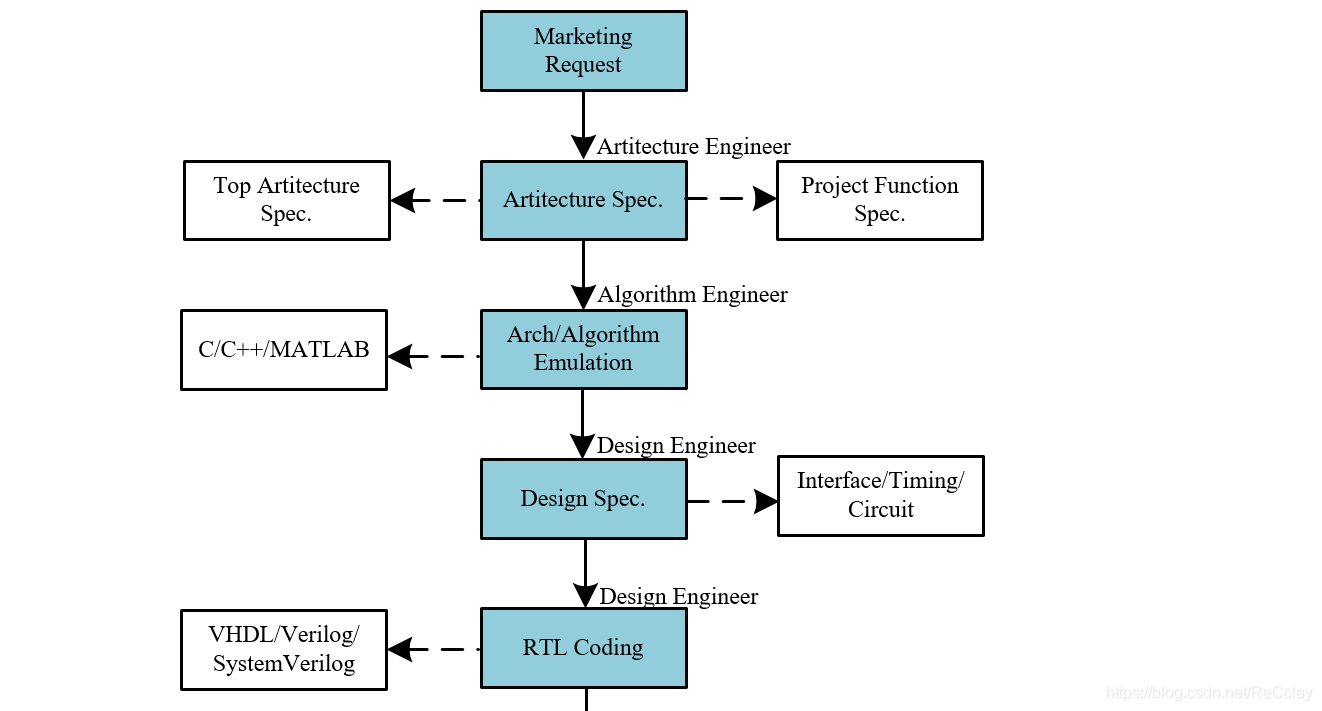
【数字IC验证快速入门】3、数字IC设计全流程介绍
欢迎来战,赢取丰厚奖金:Code Golf 代码高尔夫挑战赛正式启动
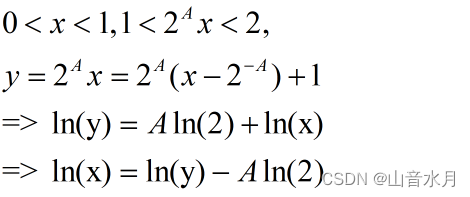
计算lnx的一种方式
死信队列入门(两个消费者,一个生产者)
随机推荐
微信小程序正则表达式提取链接
实操演示:产研团队如何高效构建需求工作流?
计算lnx的一种方式
【数字IC验证快速入门】1、浅谈数字IC验证,了解专栏内容,明确学习目标
常用的视图容器类组件
19 mongoose modularization
Notes on key vocabulary in the English original of the biography of jobs (12) [chapter ten & eleven]
本季度干货导航 | 2022年Q2
Codeforces Round #804 (Div. 2) - A, B, C
A way to calculate LNX
Leetcode skimming: binary tree 16 (path sum)
Y57. Chapter III kubernetes from entry to proficiency -- business image version upgrade and rollback (30)
document方法
【数字IC验证快速入门】3、数字IC设计全流程介绍
How to retrieve the root password of MySQL if you forget it
Elk distributed log analysis system deployment (Huawei cloud)
mongodb/文档操作
【数字IC验证快速入门】9、Verilog RTL设计必会的有限状态机(FSM)
JS implementation prohibits web page zooming (ctrl+ mouse, +, - zooming effective pro test)
Mysql频繁操作出现锁表问题