当前位置:网站首页>Luogu p4127 [ahoi2009] similar distribution problem solution
Luogu p4127 [ahoi2009] similar distribution problem solution
2022-07-06 07:29:00 【q779】
Luogu P4127 [AHOI2009] The same kind of distribution Answer key
Topic link :P4127 [AHOI2009] The same kind of distribution
The question :
Give two numbers a , b a,b a,b , Find out [ a , b ] [a,b] [a,b] The sum of the numbers in can divide the number of the original number .
For all the data , 1 ≤ a ≤ b ≤ 1 0 18 1 ≤ a ≤ b ≤ 10^{18} 1≤a≤b≤1018.
Tomorrow is the final exam, not only do not review, but also brush questions qwqqwqwq
Because we can't know the digit sum of each number exactly
But we know they must be [ 1 , 9 × l ] [1,9 \times l] [1,9×l] Within the scope of ( l l l Is the longest digit )
We enumerate all digit sums and calculate each digit and the corresponding answer
Add up these answers to [ 0 , x ] [0,x] [0,x] The answer
[ a , b ] [a,b] [a,b] The answer of can be split into two questions [ 0 , b ] [0,b] [0,b] and [ 0 , a − 1 ] [0,a-1] [0,a−1]
And here a , b ≤ 1 0 18 a,b \le 10^{18} a,b≤1018 , The direct press in state is obviously unacceptable
So we can consider recording the digits of the current enumeration and the numbers in the sense
Convenience , We call the sum of digits of the current enumeration m m m
set up f i , j , k f_{i,j,k} fi,j,k It means that only the former i i i digit ( Including leading zeros ), front i i i The sum of digits is j j j , Current digital analog m m m by k k k The answer is
It's not hard to find out
f i , j , k = ∑ 0 ≤ d ≤ t f i + 1 , j + d , ( k × 10 + d m o d m ) f_{i,j,k} = \sum_{0 \le d \le t} f_{i+1,j+d,\left(k\times 10 + d \, \bmod \, m\right)} fi,j,k=0≤d≤t∑fi+1,j+d,(k×10+dmodm)
among t t t For the first time i + 1 i+1 i+1 High bit limit
The search and writing method can be much simpler
Time complexity O ( 9 3 × l 4 ) O(9^3\times l^4) O(93×l4)
Code :
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iomanip>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N (int)()
int len,num[25],f[25][205][205];
int dfs(int u,int sum,int st,int limit,int p)
{
if(u>len)
{
if(!sum)return 0;
return st==0&&sum==p;
}
if(!limit&&f[u][sum][st]!=INF)
return f[u][sum][st];
int up=limit?num[len-u+1]:9;
int res=0;
for(int i=0; i<=up; i++)
res+=dfs(u+1,sum+i,(10*st+i)%p,limit&&i==up,p);
return limit?res:f[u][sum][st]=res;
}
int solve(int x)
{
int res=0; len=0;
while(x) num[++len]=x%10,x/=10;
for(int m=1; m<=9*len; m++)
{
memset(f,0x3f,sizeof(f));
res+=dfs(1,0,0,1,m);
}
return res;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
// freopen("check.in","r",stdin);
// freopen("check.out","w",stdout);
int l,r; cin >> l >> r;
cout << solve(r)-solve(l-1) << '\n';
return 0;
}
It's okay anyway whk For the time being
Reprint please explain the source
边栏推荐
- C intercept string
- Ali's redis interview question is too difficult, isn't it? I was pressed on the ground and rubbed
- Uni app practical project
- The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
- Is the super browser a fingerprint browser? How to choose a good super browser?
- 【线上问题处理】因代码造成mysql表死锁的问题,如何杀掉对应的进程
- Solution to the problem of breakthrough in OWASP juice shop shooting range
- (4) Web security | penetration testing | network security web site source code and related analysis
- C # connect to SQLite database to read content
- Seriously recommend several machine learning official account
猜你喜欢

Google可能在春节后回归中国市场。
智能终端设备加密防护的意义和措施

qt颜色与字符串、uint相互转换
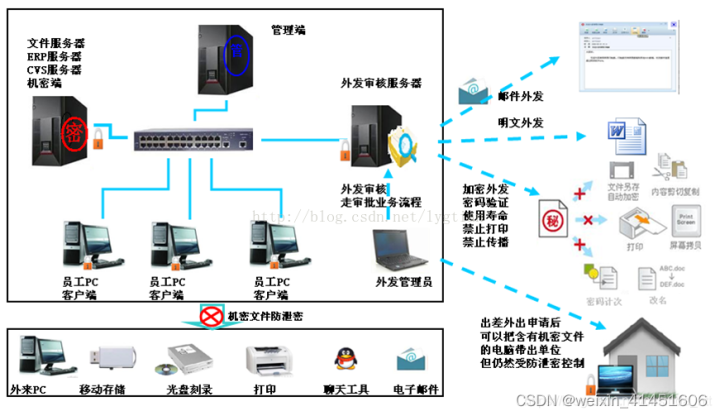
Sharing of source code anti disclosure scheme under burning scenario
SSM学习

杰理之BLE【篇】

1091: two or three things in childhood (multi instance test)
You deserve this high-value open-source third-party Netease cloud music player
![Ble of Jerry [chapter]](/img/00/27486ad68bf491997d10e387c32dd4.png)
Ble of Jerry [chapter]
![[MySQL learning notes 32] mvcc](/img/0d/2df82b63d1eb3283a84e27f67c1523.png)
[MySQL learning notes 32] mvcc
随机推荐
Set picture annotation in markdown
The way to learn go (I) the basic introduction of go to the first HelloWorld
How to delete all the words before or after a symbol in word
The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower
剪映的相关介绍
Supervisor usage document
TS 类型体操 之 extends,Equal,Alike 使用场景和实现对比
TS 类型体操 之 循环中的键值判断,as 关键字使用
After the hot update of uniapp, "mismatched versions may cause application exceptions" causes and Solutions
Brief explanation of instagram operation tips in 2022
合规、高效,加快药企数字化转型,全新打造药企文档资源中心
杰理之BLE【篇】
Ble of Jerry [chapter]
C intercept string
(4) Web security | penetration testing | network security web site source code and related analysis
NiO programming introduction
SSM learning
杰理之普通透传测试---做数传搭配 APP 通信【篇】
LeetCode Algorithm 2181. Merge nodes between zero
TypeScript 接口属性