当前位置:网站首页>浅谈函数递归汉诺塔
浅谈函数递归汉诺塔
2022-08-03 05:11:00 【宗介@bit】
前言
谈到递归相信大家都会想起一个特别经典的问题——汉诺塔。本文浅谈一下自己对汉诺塔问题的简单理解和对该问题简单思考。如有错误,请多指教!
一、汉诺塔问题是什么?
汉诺塔问题源自印度一个古老的传说,印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱,其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上,移动过程中必须遵守以下规则:
每次只能移动柱子最顶端的一个圆盘;
每个柱子上,小圆盘永远要位于大圆盘之上;
二、思考方式
1.大体思考
这个问题猛然一看感觉无从下手,我们不妨将问题简单抽象出来。我们可以简单举个小例子:
当盘子为3的时候,(为了便于描述:因为规则是大盘子在下,所以盘子从下往上命名为3 2 1;柱子状态为空为0)
起始状态
A: 3 2 1;(从下往上)
B:空
C:空
--------------
A:3 2
B:0
C :1
A: 3
B: 2
C: 1
A:3
B:2 1
C: 0
A:0
B:2 1
C:3 ;
A:1
B:2
C:3
A:1
B:0
C:3 2
A :
B :
C : 3 2 1
----------------
Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C
从上面例子简单分析:
第一步:先移动1从A到C柱上,
第二步:现在把2从A移动到B柱上,
第三步:把1从C移动动到B;
第四步:把3从A移动到C;
第五步:把1从B移动到A;
第六步:把2从B移动到C;
第七步:把1从A移动到C;
我们先通过抽象思考一下这个移动盘子的最后一步肯定是:前N-1个盘子一定在C柱子上(或者B都行只是一个代号用来举例),把此时另外某个柱子上一定有一个1号盘子,只需把这个1号盘子移动到C柱上就行了。那么前N-1个盘子是怎么到C柱的,一定有N-2个盘子移动到了C柱上,只需移动1号盘子到C柱上,便可得到N-1个盘子到C柱上,这样依此类推可以把n-1,n-2,n-3,…看成一个整体,直到把n分解成1这种简单求解的问题。
2.简单归纳
通过上述的简单思考,其实我们可以把这个相对复杂的问题简化成规模较小的问题。这种处理问题的思想叫做分治思想。分而治之,把大问题转化成小问题。但其实不难看出,该问题的处理方法都是相同的,都是重复的计算步骤,因此分治思想的前提是保证划分出来的小规模问题处理方法都是相同的。如果该问题把简单转成数学模型来求解的话,可以很自然的把n个盘子移动次数设为F(n),当A柱子上有n个盘子时候,A柱上除了n号盘子以外的前n-1个盘子都会通过某种方式移动到B柱子上;A上最大的盘子N号盘子移动一次到C柱,B上的n-1个盘子通过某种方式移动到C柱上,所以一共有2F(n-1)+1次,当n=1时,可以明显看出只需移动一次,于是即可得到表达式F(n)=2F(n-1)+1,F(1)=1;这便推导出了递归表达式,有了该式子可以很容易写出递归函数。
3.函数递归的实现
写递归首先找到边界条件,也就是递归出口,这样才不会死递归,递归出口就是n=1的时候,直接一次移动。当n>1时实际上是上面表达式中调用了两次F(n-1),所以在写递归时须在函数内部写两次(n-1)的情景。
#include<stdio.h>
void hanoi(int n, char A, char C, char B)
{
if (n == 1)
printf("Move disk %d from %c to %c\n", n, A, C);
else
{
hanoi(n - 1, A, B, C);
printf("Move disk %d from %c to %c\n", n, A, C);
hanoi(n - 1, B, C, A);
}
}
int main()
{
int n;
scanf("%d", &n);
hanoi(n, 'A', 'C', 'B');
return 0;
}
``
总结
其实,如果有兴趣的话是可以推导出证明出来F(n)的详细表达式的,因为F(1)=1,F(n)=2*F(n-1)+1;
可以得到F(1)=1,F(2)=3,F(3)=7,F(4)=15…其实F(n)=2^n-1。这是可以证明出来的,但是以上主要还是想介绍函数递归的使用,以及用分治思想来处理解决一些问题。以上便是我的拙见,如有错误,请多指教!
边栏推荐
猜你喜欢
力扣561. 数组拆分

High availability, two locations and three centers
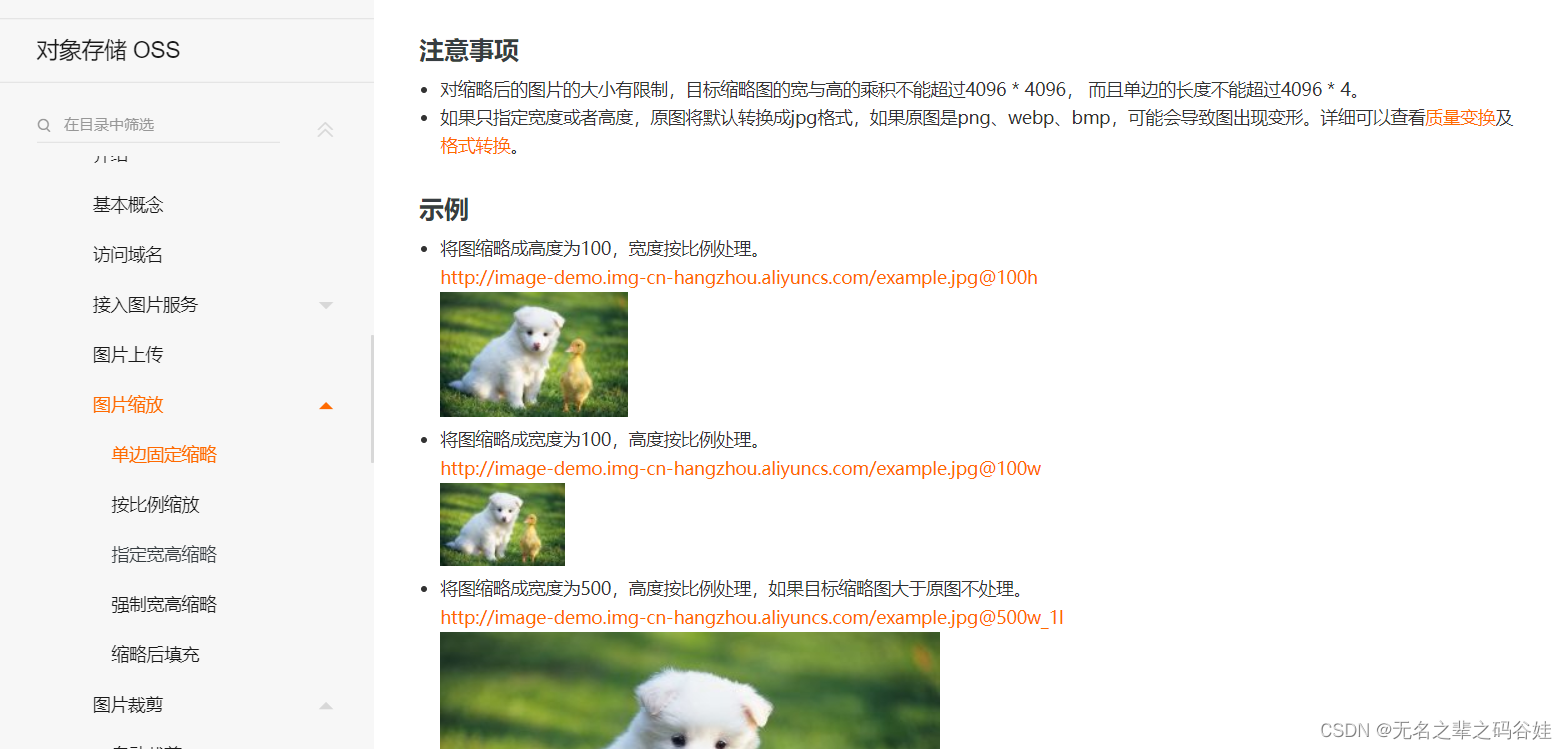
阿里云对象存储oss私有桶生成链接

13.
lt.647. Palindromic substring + lt.516. Longest palindrome subsequence 
ModelArts第二次培训
网络流媒体下载的 10 种方法(以下载 Echo 音乐为例)
Kaggle(四)Scikit-learn
Modelarts第一次培训
UV decomposition of biotin - PEG2 - azide | CAS: 1192802-98-4 biotin connectors
用C语言来实现扫雷小游戏
随机推荐
VSO Downloader Ultimate 5.0.1.45 中文多语免费版 在线视频下载工具
-完全数-
HarmonyOS应用开发培训第二次作业
mysql 存储过程 动态参数 查询执行结果
嵌入式-I2C-物理电路图
minio下载文件乱码或者是一条横线
Exception (abnormal) and Error (error) difference analysis
0.ROS常用命令
阿凡提的难题
7.18(7)
Newifi路由器第三方固件玩机教程,这个路由比你想的更强大以及智能_Newifi y1刷机_smzdm
Flask Web 报错:
Tag stack - stack monotonically preparatory knowledge - lt. 739. The daily temperature
Apache DolphinScheduler版本2.0.5分布式集群的安装
-一尺之棰-
Ali cloud object storage oss private barrels to generate links
Redis6学习笔记
1095 解码PAT准考证 (25 分)(C语言)
UV decomposition of biotin - PEG2 - azide | CAS: 1192802-98-4 biotin connectors
Object类与常用API
