当前位置:网站首页>Codeworks 5 questions per day (1700 average) - day 7
Codeworks 5 questions per day (1700 average) - day 7
2022-07-07 03:42:00 【Soup key TJ】
Multicolored Cars
Topic translation
【 Title Description 】
Definition c n t x ( i ) cnt_{x}(i) cntx(i) To i i i moment x x x The number of occurrences .
Now give n n n Number a 1 , a 2 … … a n a_{1},a_{2}……a_{n} a1,a2……an, a i a_{i} ai It means the moment i i i Number of occurrences . A l i c e Alice Alice Selected a number m m m, Please help B o b Bob Bob Choose a number k k k, Make for any moment i i i, There are c n t k ( i ) > = c n t m ( i ) cnt_{k}(i)>=cnt_{m}(i) cntk(i)>=cntm(i). If there is no such k k k Please export − 1 -1 −1.
【 Input format 】
The first line has two integers n n n, m m m, Express n n n Number , A l i c e Alice Alice Number selected m m m.
The second line n n n It's an integer a 1 , a 2 … … a n a_{1},a_{2}……a_{n} a1,a2……an, a i a_{i} ai It means the moment i i i Number of occurrences .
【 Output format 】
There is such k k k Please output any feasible solution , If there is no such k k k Please export − 1 -1 −1.
【 Data range 】
No more than 1 0 6 10^6 106
Title Description
Alice and Bob got very bored during a long car trip so they decided to play a game.
From the window they can see cars of different colors running past them. Cars are going one after another.
The game rules are like this.
Firstly Alice chooses some color A A A , then Bob chooses some color B B B ( A ≠ B A≠B A=B ).
After each car they update the number of cars of their chosen color that have run past them.
Let’s define this numbers after i i i -th car c n t A ( i ) cnt_{A}(i) cntA(i) and c n t B ( i ) cnt_{B}(i) cntB(i) .
- If KaTeX parse error: Expected 'EOF', got '&' at position 11: cnt_{A}(i)&̲gt;cnt_{B}(i) for every i i i then the winner is Alice.
- If c n t B ( i ) > = c n t A ( i ) cnt_{B}(i)>=cnt_{A}(i) cntB(i)>=cntA(i) for every i i i then the winner is Bob.
- Otherwise it’s a draw.
Bob knows all the colors of cars that they will encounter and order of their appearance.
Alice have already chosen her color A A A and Bob now wants to choose such color B B B that he will win the game (draw is not a win).
Help him find this color.
If there are multiple solutions, print any of them.
If there is no such color then print -1.
Input format
The first line contains two integer numbers n n n and A A A ( 1 < = n < = 1 0 5 , 1 < = A < = 1 0 6 1<=n<=10^{5},1<=A<=10^{6} 1<=n<=105,1<=A<=106 ) – number of cars and the color chosen by Alice.
The second line contains n n n integer numbers c 1 , c 2 , . . . , c n c_{1},c_{2},...,c_{n} c1,c2,...,cn ( 1 < = c i < = 1 0 6 1<=c_{i}<=10^{6} 1<=ci<=106 ) — colors of the cars that Alice and Bob will encounter in the order of their appearance.
Output format
Output such color B B B ( 1 < = B < = 1 0 6 1<=B<=10^{6} 1<=B<=106 ) that if Bob chooses it then he will win the game.
If there are multiple solutions, print any of them.
If there is no such color then print -1.
It is guaranteed that if there exists any solution then there exists solution with ( 1 < = B < = 1 0 6 1<=B<=10^{6} 1<=B<=106 ).
Examples #1
The sample input #1
4 1
2 1 4 2
Sample output #1
2
Examples #2
The sample input #2
5 2
2 2 4 5 3
Sample output #2
-1
Examples #3
The sample input #3
3 10
1 2 3
Sample output #3
4
Tips
Let’s consider availability of colors in the first example:
- c n t 2 ( i ) > = c n t 1 ( i ) cnt_{2}(i)>=cnt_{1}(i) cnt2(i)>=cnt1(i) for every i i i , and color 2 2 2 can be the answer.
- KaTeX parse error: Expected 'EOF', got '&' at position 11: cnt_{4}(2)&̲lt;cnt_{1}(2) , so color 4 4 4 isn’t the winning one for Bob.
- All the other colors also have KaTeX parse error: Expected 'EOF', got '&' at position 11: cnt_{j}(2)&̲lt;cnt_{1}(2) , thus they are not available.
In the third example every color is acceptable except for 10 10 10 .
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
int n,m,k,a[1000005],mmax,signm=0;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
scanf("%d",&k);
mmax=max(mmax,k);
if(k==m){
signm++;
}
else if(a[k]>=signm){
a[k]++;
}
}
for(int i=1;i<=mmax;i++){
if(a[i]>=signm&&m!=i){
cout<<i;
return 0;
}
}
puts("-1");
return 0;
}
Remove Extra One
Topic translation
Give a length of n Permutation p, Find an element , So that the elements are arranged after taking this element out of the arrangement “records” most .
One "record" Is an element a i a_i ai Satisfy : For each positive integer 1 ≤ j < i 1\le j <i 1≤j<i , a i > a j a_i > a_j ai>aj.
Title Description
You are given a permutation p p p of length n n n .
Remove one element from permutation to make the number of records the maximum possible.
We remind that in a sequence of numbers a 1 , a 2 , . . . , a k a_{1},a_{2},...,a_{k} a1,a2,...,ak the element a i a_{i} ai is a record if for every integer j j j ( KaTeX parse error: Expected 'EOF', got '&' at position 5: 1<=j&̲lt;i ) the following holds: KaTeX parse error: Expected 'EOF', got '&' at position 6: a_{j}&̲lt;a_{i} .
Input format
The first line contains the only integer n n n ( 1 < = n < = 1 0 5 1<=n<=10^{5} 1<=n<=105 ) — the length of the permutation.
The second line contains n n n integers p 1 , p 2 , . . . , p n p_{1},p_{2},...,p_{n} p1,p2,...,pn ( 1 < = p i < = n 1<=p_{i}<=n 1<=pi<=n ) — the permutation.
All the integers are distinct.
Output format
Print the only integer — the element that should be removed to make the number of records the maximum possible.
If there are multiple such elements, print the smallest one.
Examples #1
The sample input #1
1
1
Sample output #1
1
Examples #2
The sample input #2
5
5 1 2 3 4
Sample output #2
5
Tips
In the first example the only element can be removed.
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
ll n,a[N],sign[N],x=0,y=0,k;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
}
for(int i=1;i<=n;i++){
if(a[i]>a[y]){
x=y;
y=i;
sign[i]--;
}
else if(a[i]>a[x]){
x=i;
sign[y]++;
}
}
k=1;
for(int i=2;i<=n;i++){
if(sign[i]>sign[k]||(sign[i]==sign[k]&&a[i]<a[k])){
k=i;
}
}
cout<<a[k]<<endl;
return 0;
}
The Meaningless Game
Topic translation
Slastyona And her loyal dog pushk are playing a meaningless but interesting game . The game includes multiple rounds .
Its rules are very simple : First choose a natural number k. then , Who says ( Or bark ) If you are faster than the other one, you will win a game .
The winner's score will be multiplied by k The square of , The score of the loser can only be multiplied by k. At the beginning of the game ,Slastyona and PurSok Have an initial score .
Unfortunately ,Slastyona I lost my notepad , There is a record of what they have played N History of games .
She managed to recall the final result of each match , But the memory is very vague .
help Slastyona Verify their correctness , perhaps , let me put it another way , For each pair of given scores , Determine whether the game can achieve such a result .
Title Description
 Slastyona and her loyal dog Pushok are playing a meaningless game that is indeed very interesting.
Slastyona and her loyal dog Pushok are playing a meaningless game that is indeed very interesting.
The game consists of multiple rounds.
Its rules are very simple: in each round, a natural number k k k is chosen.
Then, the one who says (or barks) it faster than the other wins the round.
After that, the winner’s score is multiplied by k 2 k^{2} k2 , and the loser’s score is multiplied by k k k .
In the beginning of the game, both Slastyona and Pushok have scores equal to one.
Unfortunately, Slastyona had lost her notepad where the history of all n n n games was recorded.
She managed to recall the final results for each games, though, but all of her memories of them are vague.
Help Slastyona verify their correctness, or, to put it another way, for each given pair of scores determine whether it was possible for a game to finish with such result or not.
Input format
In the first string, the number of games n n n ( 1 < = n < = 350000 ) (1<=n<=350000) (1<=n<=350000) is given.
Each game is represented by a pair of scores a a a , b b b ( 1 < = a , b < = 1 0 9 ) (1<=a,b<=10^{9}) (1<=a,b<=109) – the results of Slastyona and Pushok, correspondingly.
Output format
For each pair of scores, answer “Yes” if it’s possible for a game to finish with given score, and “No” otherwise.
You can output each letter in arbitrary case (upper or lower).
Examples #1
The sample input #1
6
2 4
75 45
8 8
16 16
247 994
1000000000 1000000
Sample output #1
Yes
Yes
Yes
No
No
Yes
Tips
First game might have been consisted of one round, in which the number 2 2 2 would have been chosen and Pushok would have won.
The second game needs exactly two rounds to finish with such result: in the first one, Slastyona would have said the number 5 5 5 , and in the second one, Pushok would have barked the number 3 3 3 .
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
ll n,a,b,c;
int main(){
cin>>n;
while(n--){
scanf("%lld %lld",&a,&b);
ll s=a*b;
c=round(pow(1.0*s,1.0/3));
if(c*c*c==s&&a%c==0&&b%c==0){
puts("Yes");
}
else puts("No");
}
return 0;
}
Posterized
Topic translation
Give a set of numbers , Divide this group of numbers into consecutive groups , The number of each group shall not exceed k, All numbers in each group are assigned to the smallest number in the Group , Find the case where this group of numbers has the smallest canonical order
Title Description
Professor Ibrahim has prepared the final homework for his algorithm’s class.
He asked his students to implement the Posterization Image Filter.
Their algorithm will be tested on an array of integers, where the i i i -th integer represents the color of the i i i -th pixel in the image.
The image is in black and white, therefore the color of each pixel will be an integer between 0 and 255 (inclusive).
To implement the filter, students are required to divide the black and white color range [0, 255] into groups of consecutive colors, and select one color in each group to be the group’s key.
In order to preserve image details, the size of a group must not be greater than k k k , and each color should belong to exactly one group.
Finally, the students will replace the color of each pixel in the array with that color’s assigned group key.
To better understand the effect, here is an image of a basking turtle where the Posterization Filter was applied with increasing k k k to the right.
 To make the process of checking the final answer easier, Professor Ibrahim wants students to divide the groups and assign the keys in a way that produces the lexicographically smallest possible array.
To make the process of checking the final answer easier, Professor Ibrahim wants students to divide the groups and assign the keys in a way that produces the lexicographically smallest possible array.
Input format
The first line of input contains two integers n n n and k k k ( 1 ≤ n ≤ 1 0 5 1 \leq n \leq 10^5 1≤n≤105 , 1 ≤ k ≤ 256 1 \leq k \leq 256 1≤k≤256 ), the number of pixels in the image, and the maximum size of a group, respectively.
The second line contains n n n integers p 1 , p 2 , … , p n p_1, p_2, \dots, p_n p1,p2,…,pn ( 0 ≤ p i ≤ 255 0 \leq p_i \leq 255 0≤pi≤255 ), where p i p_i pi is the color of the i i i -th pixel.
Output format
Print n n n space-separated integers;
the lexicographically smallest possible array that represents the image after applying the Posterization filter.
Examples #1
The sample input #1
4 3
2 14 3 4
Sample output #1
0 12 3 3
Examples #2
The sample input #2
5 2
0 2 1 255 254
Sample output #2
0 1 1 254 254
Tips
One possible way to group colors and assign keys for the first sample:
Color 2 2 2 belongs to the group [ 0 , 2 ] [0,2] [0,2] , with group key 0 0 0 .
Color 14 14 14 belongs to the group [ 12 , 14 ] [12,14] [12,14] , with group key 12 12 12 .
Colors 3 3 3 and 4 4 4 belong to group [ 3 , 5 ] [3, 5] [3,5] , with group key 3 3 3 .
Other groups won’t affect the result so they are not listed here.
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
int n,k,a[N],sign[N];
int main(){
cin>>n>>k;
memset(sign,-1,sizeof(sign));
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
if(sign[a[i]]==-1){
int p=a[i]-k+1;
if(p<0) p=0;
while(sign[p]!=-1&&sign[p]!=p) p++;
for(int j=p;j<=a[i];j++) sign[j]=p;
}
}
for(int i=1;i<=n;i++){
printf("%d ",sign[a[i]]);
}
return 0;
}
Covered Points Count
Topic translation
The main idea of the topic :
Here you are. n Intervals , Find the number of layers covered by these intervals as k ( k < = n ) k(k<=n) k(k<=n) The number of points
Input format :
The first line is an integer , n n n, n < = 2 ∗ 1 0 5 n<=2*10^5 n<=2∗105
following n n n That's ok , Each line has two integers , That is, the left and right endpoints of this interval l , r ( 0 < = l < = r < = 1 0 18 ) l,r(0<=l<=r<=10^{18}) l,r(0<=l<=r<=1018)
Output format :
n n n It's an integer , That is, the number of points corresponding to the number of each covered layer
Title Description
You are given n n n segments on a coordinate line; each endpoint of every segment has integer coordinates.
Some segments can degenerate to points.
Segments can intersect with each other, be nested in each other or even coincide.
Your task is the following: for every k ∈ [ 1.. n ] k \in [1..n] k∈[1..n] , calculate the number of points with integer coordinates such that the number of segments that cover these points equals k k k .
A segment with endpoints l i l_i li and r i r_i ri covers point x x x if and only if l i ≤ x ≤ r i l_i \le x \le r_i li≤x≤ri .
Input format
The first line of the input contains one integer n n n ( 1 ≤ n ≤ 2 ⋅ 1 0 5 1 \le n \le 2 \cdot 10^5 1≤n≤2⋅105 ) — the number of segments.
The next n n n lines contain segments.
The i i i -th line contains a pair of integers l i , r i l_i, r_i li,ri ( 0 ≤ l i ≤ r i ≤ 1 0 18 0 \le l_i \le r_i \le 10^{18} 0≤li≤ri≤1018 ) — the endpoints of the i i i -th segment.
Output format
Print n n n space separated integers c n t 1 , c n t 2 , … , c n t n cnt_1, cnt_2, \dots, cnt_n cnt1,cnt2,…,cntn , where c n t i cnt_i cnti is equal to the number of points such that the number of segments that cover these points equals to i i i .
Examples #1
The sample input #1
3
0 3
1 3
3 8
Sample output #1
6 2 1
Examples #2
The sample input #2
3
1 3
2 4
5 7
Sample output #2
5 2 0
Tips
The picture describing the first example:
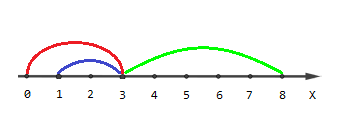
Points with coordinates [ 0 , 4 , 5 , 6 , 7 , 8 ] [0, 4, 5, 6, 7, 8] [0,4,5,6,7,8] are covered by one segment, points [ 1 , 2 ] [1, 2] [1,2] are covered by two segments and point [ 3 ] [3] [3] is covered by three segments.
The picture describing the second example:

Points [ 1 , 4 , 5 , 6 , 7 ] [1, 4, 5, 6, 7] [1,4,5,6,7] are covered by one segment, points [ 2 , 3 ] [2, 3] [2,3] are covered by two segments and there are no points covered by three segments.
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
ll n,k,l,r,s[N];
map<ll,ll> a;
map<ll,ll>::iterator it;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%lld %lld",&l,&r);
a[l]++;
a[r+1]--;
}
it=a.begin();
ll x=it->first;
ll y=it->second;
it++;
for(;it!=a.end();it++){
s[y]+=it->first-x;
x=it->first;
y+=it->second;
}
for(int i=1;i<=n;i++){
cout<<s[i]<<" ";
}
return 0;
}
边栏推荐
- SSL证书部署
- Not All Points Are Equal Learning Highly Efficient Point-based Detectors for 3D LiDAR Point
- Create applet from 0
- 腾讯云原生数据库TDSQL-C入选信通院《云原生产品目录》
- PIP download only, not install
- U.S. Air Force Research Laboratory, "exploring the vulnerability and robustness of deep learning systems", the latest 85 page technical report in 2022
- HMS core machine learning service creates a new "sound" state of simultaneous interpreting translation, and AI makes international exchanges smoother
- PHP lightweight Movie Video Search Player source code
- VHDL implementation of arbitrary size matrix addition operation
- 【达梦数据库】备份恢复后要执行两个sql语句
猜你喜欢
Confirm the future development route! Digital economy, digital transformation, data This meeting is very important
Open3d mesh filtering
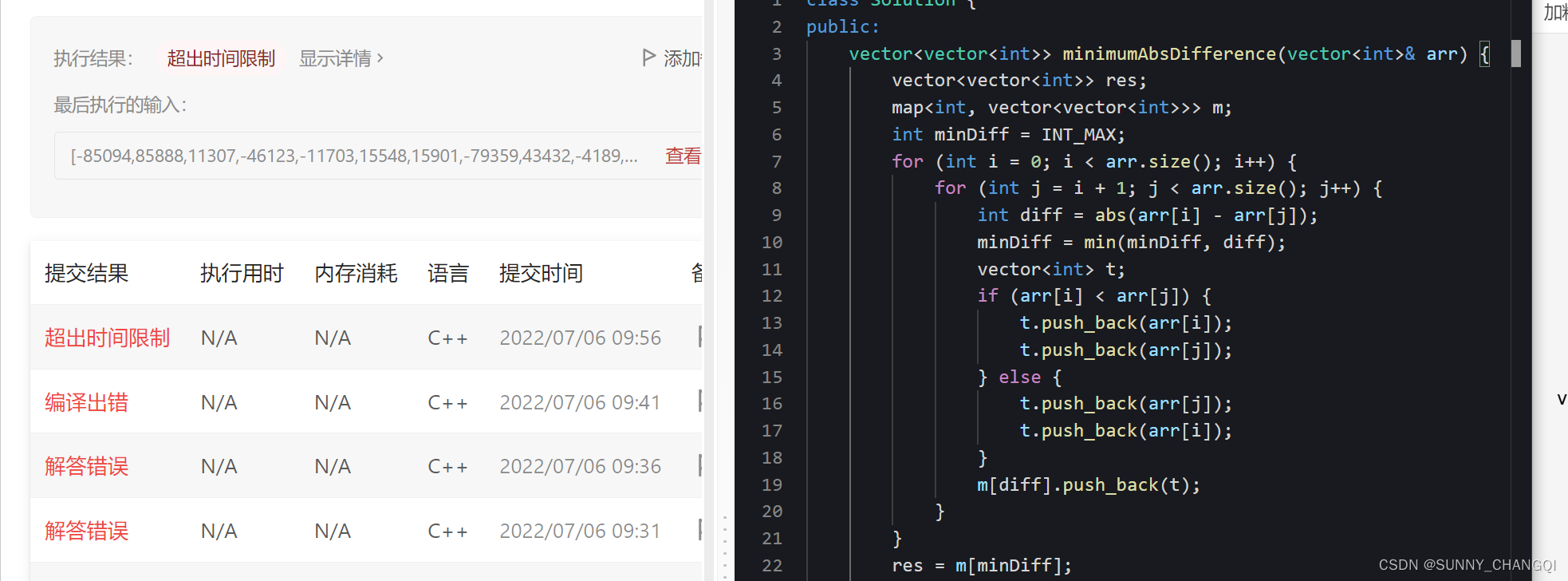
1200.Minimum Absolute Difference

树莓派设置静态ip
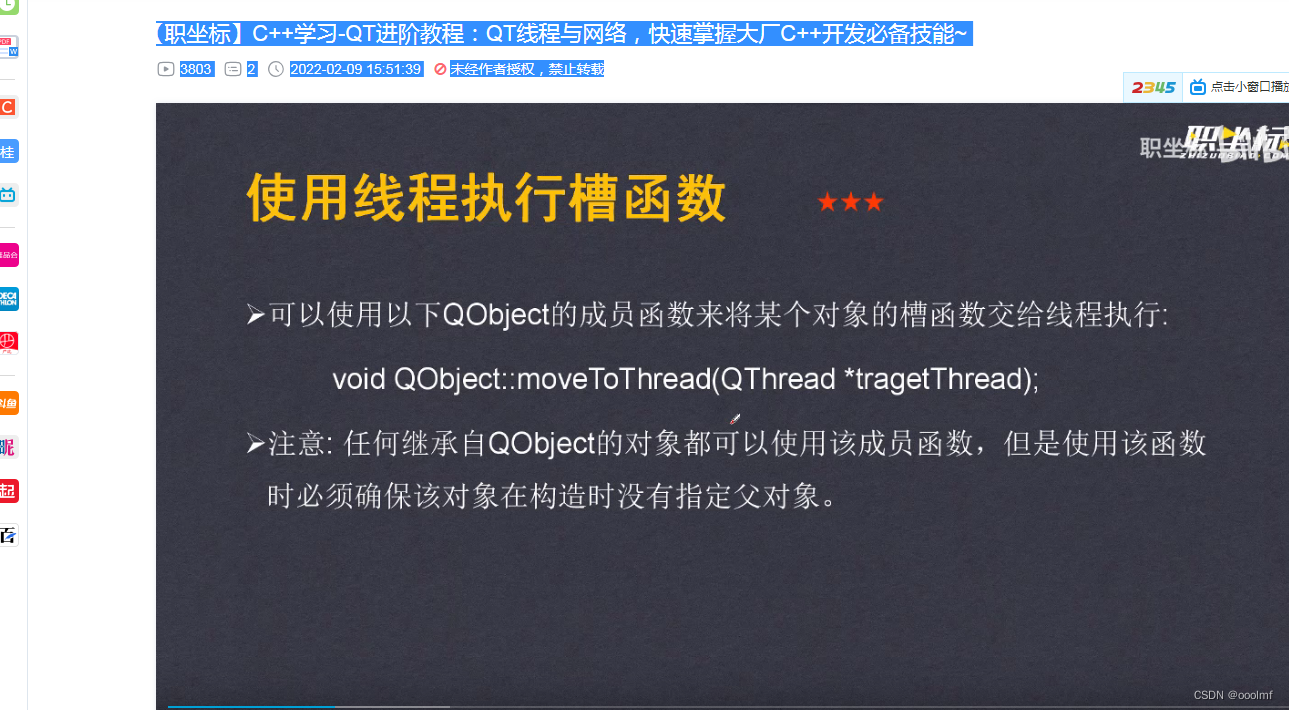
qt-线程等01概念
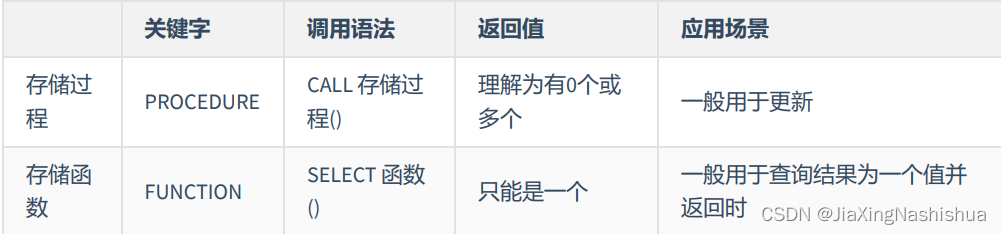
Stored procedures and functions (MySQL)
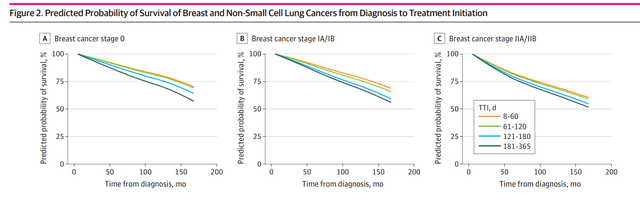
R数据分析:cox模型如何做预测,高分文章复现
Docker部署Mysql8的实现步骤
ubuntu20安装redisjson记录

VHDL implementation of arbitrary size matrix multiplication
随机推荐
密码学系列之:在线证书状态协议OCSP详解
20.(arcgis api for js篇)arcgis api for js面采集(SketchViewModel)
Tencent cloud native database tdsql-c was selected into the cloud native product catalog of the Academy of communications and communications
Stored procedures and functions (MySQL)
Under the tide of "going from virtual to real", Baidu AI Cloud is born from real
Create applet from 0
Install torch 0.4.1
sshd[12282]: fatal: matching cipher is not supported: aes256- [email protected] [preauth]
Confirm the future development route! Digital economy, digital transformation, data This meeting is very important
Introduction to opensea platform developed by NFT trading platform (I)
Appx code signing Guide
Clock in during winter vacation
Graphical tools package yolov5 and generate executable files exe
什么是 BA ?BA怎么样?BA和BI是什么关系?
[leetcode] 700 and 701 (search and insert of binary search tree)
如何自定义Latex停止运行的快捷键
华为小米互“抄作业”
Mobile measurement and depth link platform - Branch
PHP lightweight Movie Video Search Player source code
[Dameng database] after backup and recovery, two SQL statements should be executed