当前位置:网站首页>01tire+链式前向星+dfs+贪心练习题.1
01tire+链式前向星+dfs+贪心练习题.1
2022-07-07 14:11:00 【汤键.TJ】
最长异或路径
题目描述
给定一棵 n n n 个点的带权树,结点下标从 1 1 1 开始到 n n n。寻找树中找两个结点,求最长的异或路径。
异或路径指的是指两个结点之间唯一路径上的所有边权的异或。
输入格式
第一行一个整数 n n n,表示点数。
接下来 n − 1 n-1 n−1 行,给出 u , v , w u,v,w u,v,w ,分别表示树上的 u u u 点和 v v v 点有连边,边的权值是 w w w。
输出格式
一行,一个整数表示答案。
样例 #1
样例输入 #1
4
1 2 3
2 3 4
2 4 6
样例输出 #1
7
提示
最长异或序列是 1 , 2 , 3 1,2,3 1,2,3,答案是 7 = 3 ⊕ 4 7=3\oplus 4 7=3⊕4。
数据范围
1 ≤ n ≤ 100000 ; 0 < u , v ≤ n ; 0 ≤ w < 2 31 1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31} 1≤n≤100000;0<u,v≤n;0≤w<231。
过程全部在注释内
#include<bits/stdc++.h>
using namespace std;
const int N=6e5+10;
typedef long long ll;
int son[N][2],idx=1,s=0;
int n,head[N],dis[N],nt[N],to[N],weight[N],cnt;
void add(int u,int v,int w){
//链式前向星加边
nt[++cnt]=head[u];
head[u] = cnt;
to[cnt]=v;
weight[cnt]=w;
}
void insert(int k){
int p=1;
for(int i=30;i>=0;i--){
//由于题目范围w<2^31,所以对于异或和只需要30位即可
int u=k>>i&1;//得到k的第i个二进制位的值
if(!son[p][u]) son[p][u]=++idx;//查看当前节点p的子节点u是否已给予编号,没有则标记给予编号
p=son[p][u];//移至下一节点转换位置
}
}
void dodo(int k){
int p=1,da=0;
for(int i=30;i>=0;i--){
int u=k>>i&1;//得到k的第i个二进制位的值
//当前在trie树的节点u; u的两个儿子是son[u][0/1];
//我们贪心的考虑
//trie树从顶向下,对应着二进制位从高到低
//而我们希望高的二进制位尽可能异或出来是1
//也就是说我们在trie树从根往下走的过程中,要尽量选择能让当前这一位异或得到1的路径
if(son[p][u^1]){
//异或有异或两个相同数等于没异或的特点; 为了让这一位异或得到1,我们下一层遍历就需要去son[p][u^1]
p=son[p][u^1];//存在son[p][u^1],则贪心选择并移至下一节点转换位置
da|=(1<<i);//da存储答案,此处将da的第i个二进制位赋1
}
else p=son[p][u];//如果实在不存在son[p][u^1],我们就只能放弃这一位,去son[p][u]
}
s=max(s,da);//更新答案
}
void dfs(int u,int v){
//求dis数组做转化用
insert(dis[u]);//将此值二进制各位数插入trie树中
dodo(dis[u]);//从顶向下,贪心选择,更新答案
for(int i=head[u];i;i=nt[i]){
//遍历以i为起点的边
int vv=to[i];//到达点
if(vv==v) continue;
dis[vv]=dis[u]^weight[i];//进行两个结点之间唯一路径上的所有边权的异或
dfs(vv,u);//继续深入遍历
}
}
int main(){
cin>>n;
for(int i=1;i<n;i++){
int u,v,w;
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);//链式前向星加双向边,无论有向无向
add(v,u,w);
}
dfs(1,0);//题目所示,结点从1开始
cout<<s;
return 0;
}
边栏推荐
- Mysql database backup script
- 2022第四届中国(济南)国际智慧养老产业展览会,山东老博会
- Odoo集成Plausible埋码监控平台
- Xcode Revoke certificate
- 招标公告:福建省农村信用社联合社数据库审计系统采购项目(重新招标)
- What are compiled languages and interpreted languages?
- Leetcode-136-只出现一次的数(用异或来解答)
- 神经网络c语言中的指针是怎么回事
- Eye of depth (VI) -- inverse of matrix (attachment: some ideas of logistic model)
- iptables只允许指定ip地址访问指定端口
猜你喜欢
Numpy --- basic learning notes

Dotween -- ease function
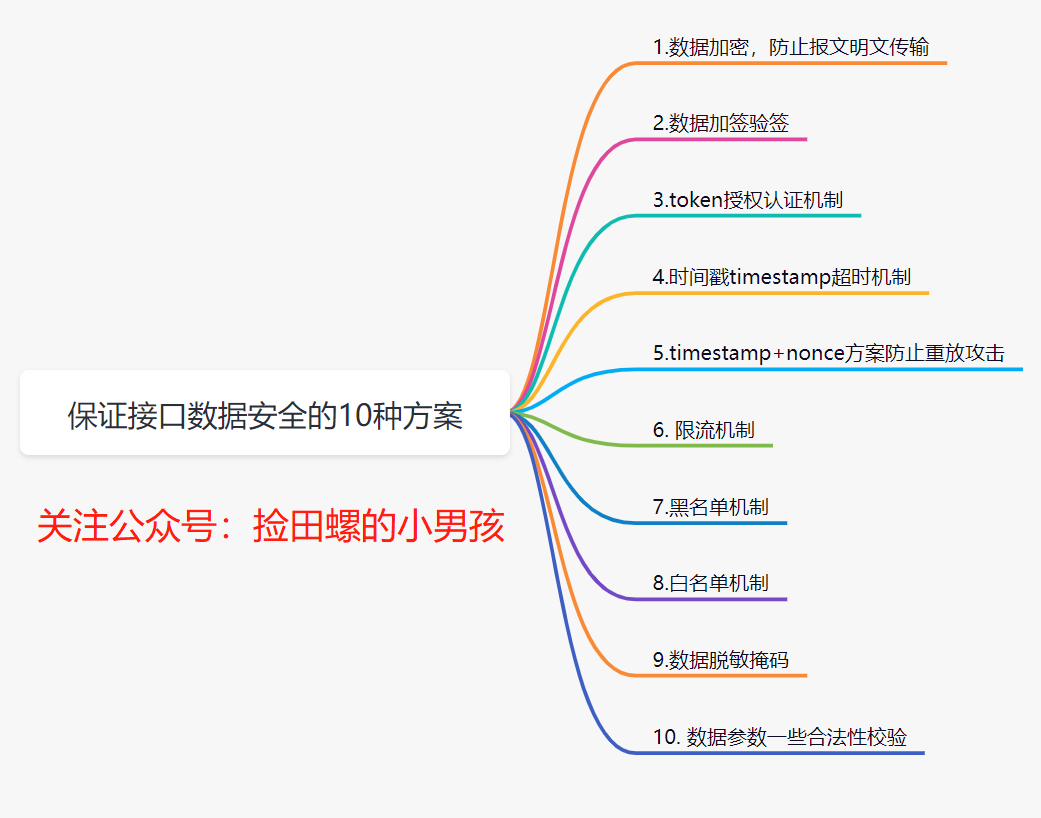
10 schemes to ensure interface data security
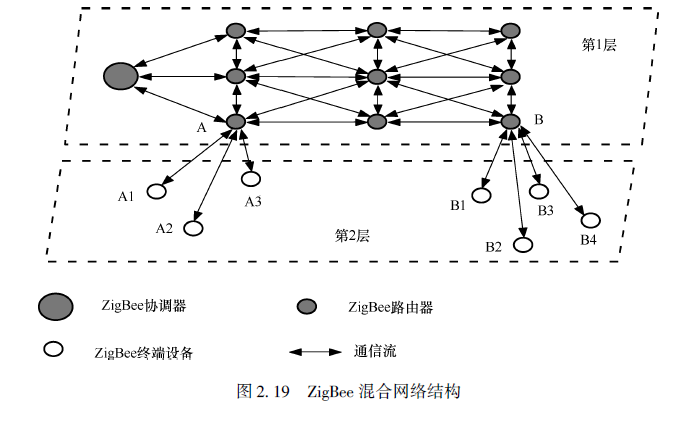
Wireless sensor networks -- ZigBee and 6LoWPAN

持续创作,还得靠它!
统计学习方法——感知机

Shipping companies' AI products are mature, standardized and applied on a large scale. CIMC, the global leader in port and shipping AI / container AI, has built a benchmark for international shipping
C4D learning notes 1- animation - animation key frames
C4D learning notes 3- animation - animation rendering process case

星瑞格数据库入围“2021年度福建省信息技术应用创新典型解决方案”
随机推荐
讲师征集令 | Apache SeaTunnel(Incubating) Meetup 分享嘉宾火热招募中!
121. 买卖股票的最佳时机
Mysql database basic operation DQL basic query
Three. JS introductory learning notes 13: animation learning
C4D learning notes 1- animation - animation key frames
iptables只允许指定ip地址访问指定端口
Enterprise log analysis system elk
hellogolang
Three. JS introductory learning notes 10:three JS grid
统计学习方法——感知机
Step by step monitoring platform ZABBIX
分步式监控平台zabbix
How to implement backspace in shell
Balanced binary tree (AVL)
记一次项目的迁移过程
修改配置文件后tidb无法启动
尤雨溪,来了!
用手机在通达信上开户靠谱吗?这样炒股有没有什么安全隐患
模仿企业微信会议室选择
Numpy --- basic learning notes