当前位置:网站首页>Codeforces Round #804 (Div. 2) - A, B, C
Codeforces Round #804 (Div. 2) - A, B, C
2022-07-05 20:23:00 【Dimple】
https://codeforces.com/contest/1699
C. The Third Problem
The question
Given a 0 0 0 To n − 1 n-1 n−1 The whole arrangement , Ask how many 0 0 0 To n − 1 n-1 n−1 The full arrangement of is similar to this arrangement ?
The answer is right 1e9+7 modulus .
Similarity definition : If two full permutations meet the following conditions , Let's say that the two are similar in full arrangement .
- For any interval [ l , r ] ( 1 ≤ l ≤ r ≤ n ) [l, r] (1 \le l \le r \le n) [l,r](1≤l≤r≤n) All satisfied with : MEX ( [ a l , a l + 1 , … , a r ] ) = MEX ( [ b l , b l + 1 , … , b r ] ) \operatorname{MEX}([a_l,a_{l+1},\ldots,a_r])=\operatorname{MEX}([b_l,b_{l+1},\ldots,b_r]) MEX([al,al+1,…,ar])=MEX([bl,bl+1,…,br])
For a pile of numbers c 1 , c 2 , … , c k c_1,c_2,\ldots,c_k c1,c2,…,ck Of MEX \operatorname{MEX} MEX Refer to , In collection c c c The first non negative integer that does not appear in x x x.
Ideas
from 0 To n-1, Count one by one , See where it can be placed . Multiplication of all possible positions is the answer .
Number of tags x The position in the original arrangement is p[x].
- First, it's easy to determine ,0 and 1 The position in a similar arrangement does not change , All for
p[0]. set uplIs the left end position ,rIs the right end position . - about 2:
1. Ifp[2]be located[l, r]in , that 2 Can be placed in[l, r]All free locations in ;
(2 Originally in[l, r]in , that MEX [ l , r ] \operatorname{MEX}[l, r] MEX[l,r] To achieve 3 了 , So in a similar arrangement 2 Only on the[l, r]in )
2. otherwise ,2 It can only be placed in its original positionp[2]; thenp[2]takelperhapsrto update ;
(2 Originally in[l, r]outside , that MEX [ l , r ] \operatorname{MEX}[l, r] MEX[l,r] It can only reach 2,2 Can't be in[l, r]in ; And if its position changes , There will be intervals MEX Value change , So in this case 2 The position of the cannot be changed ) - about 3:
1. Ifp[3]be located[l, r]in , that 3 Can be placed in[l, r]All free locations in ;
2. otherwise ,3 It can only be placed in its original positionp[3]; thenp[3]takelperhapsrto update ; - …
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N], p[N];
signed main(){
Ios;
cin >> T;
while(T--)
{
cin >> n;
for(int i=1;i<=n;i++) cin >> a[i], p[a[i]] = i;
int ans = 1;
int l = min(p[0], p[1]), r = max(p[0], p[1]);
for(int i=2;i<n;i++)
{
if(p[i] > l && p[i] < r)
{
ans = ans * (r-l+1 - i) % mod;
}
else{
if(p[i] < l) l = p[i];
else r = p[i];
}
}
cout << ans << endl;
}
return 0;
}
Experience
When there is no idea, you should calm down and push back bit by bit from the initial situation , Maybe there is a way to push .
Instead of looking at the sample and thinking ..
B. Almost Ternary Matrix
The question
Construct a n*m Of 01 matrix , bring :
- For each location , In its directly adjacent position , There are exactly two locations that are different from this location element .
2 ≤ n , m ≤ 50 2 \le n,m \le 50 2≤n,m≤50 And all are even .
Ideas
So constructed :
6 8
1 0 0 1 1 0 0 1
0 1 1 0 0 1 1 0
0 1 1 0 0 1 1 0
1 0 0 1 1 0 0 1
1 0 0 1 1 0 0 1
0 1 1 0 0 1 1 0
Code
#include<bits/stdc++.h>
using namespace std;
const int N = 210, mod = 1e9+7;
int T, n, m;
int a[N] = {
1, 0, 0, 1}, b[N] = {
0, 1, 1, 0};
int ans[N][N];
signed main(){
scanf("%d", &T);
while(T--)
{
scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++)
{
for(int j=0;j<m;j++)
{
if(i%4 == 1 || i%4 == 0) ans[i][j] = a[j%4];
else ans[i][j] = b[j%4];
}
}
for(int i=1;i<=n;i++){
for(int j=0;j<m;j++){
printf("%d ", ans[i][j]);
}
printf("\n");
}
}
return 0;
}
A. The Third Three Number Problem
The question
Give a number n n n, Find three numbers a , b , c a, b, c a,b,c Satisfy :
- ( a ⊕ b ) + ( b ⊕ c ) + ( a ⊕ c ) = n (a\oplus b)+(b\oplus c)+(a\oplus c)=n (a⊕b)+(b⊕c)+(a⊕c)=n
Output not found − 1 -1 −1.
1 ≤ n ≤ 1 0 9 , 0 ≤ a , b , c ≤ 1 0 9 1 \le n \le 10^9,\ 0 \le a, b, c \le 10^9 1≤n≤109, 0≤a,b,c≤109
Ideas
from a + b = a ⊕ b + 2 ⋅ ( a a + b = a \oplus b + 2 \cdot (a a+b=a⊕b+2⋅(a & b ) b) b) You know , a ⊕ b a \oplus b a⊕b and a + b a + b a+b Having the same parity .
that n = ( a ⊕ b ) + ( b ⊕ c ) + ( a ⊕ c ) n = (a\oplus b)+(b\oplus c)+(a\oplus c) n=(a⊕b)+(b⊕c)+(a⊕c) Just like ( a + b ) + ( b + c ) + ( a + c ) = 2 ⋅ ( a + b + c ) (a+b) + (b+c) + (a+c) =2 \cdot (a+b+c) (a+b)+(b+c)+(a+c)=2⋅(a+b+c) Having the same parity , It must be an even number .
- When n by Odd number output -1.
- otherwise Make b = c = 0 b=c=0 b=c=0, Then the original formula becomes : a + a = n a + a = n a+a=n, that a = n 2 a = \frac n 2 a=2n.
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
const int N = 200010, mod = 1e9+7;
int T, n, m;
int a[N];
signed main(){
Ios;
cin >> T;
while(T--)
{
cin >> n;
if(n % 2 == 0) cout << n/2 << " " << 0 << " " << 0 << endl;
else cout << -1 << endl;
}
return 0;
}
Experience
Focus on special circumstances .
边栏推荐
- 炒股开户最低佣金,低佣金开户去哪里手机上开户安全吗
- Leetcode: binary tree 15 (find the value in the lower left corner of the tree)
- 强化学习-学习笔记4 | Actor-Critic
- 618 "low key" curtain call, how can baiqiushangmei join hands with the brand to cross the "uncertain era"?
- 【愚公系列】2022年7月 Go教学课程 004-Go代码注释
- 银河证券在网上开户安全吗?
- Leetcode(695)——岛屿的最大面积
- 【数字IC验证快速入门】6、Questasim 快速上手使用(以全加器设计与验证为例)
- ICTCLAS word Lucene 4.9 binding
- 【数字IC验证快速入门】2、通过一个SoC项目实例,了解SoC的架构,初探数字系统设计流程
猜你喜欢

Oracle tablespace management

实操演示:产研团队如何高效构建需求工作流?

Oracle-表空间管理
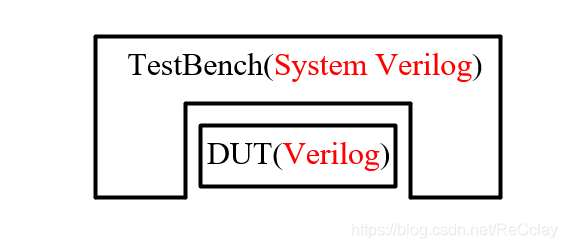
【数字IC验证快速入门】1、浅谈数字IC验证,了解专栏内容,明确学习目标
![Scala basics [HelloWorld code parsing, variables and identifiers]](/img/75/1d89581b9b8299ffb55d95514e6df4.png)
Scala basics [HelloWorld code parsing, variables and identifiers]
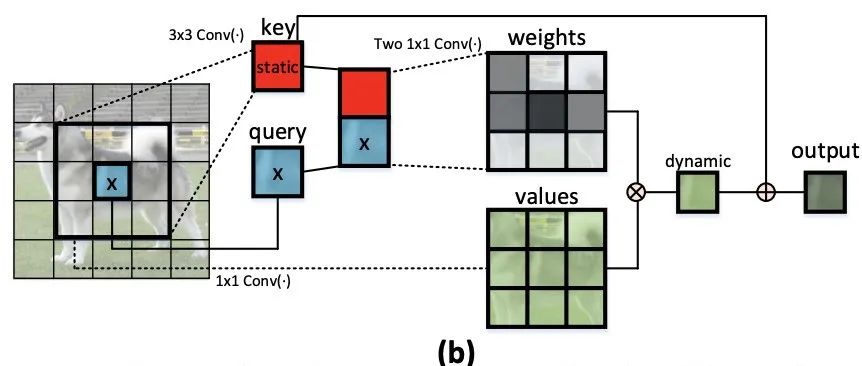
无卷积骨干网络:金字塔Transformer,提升目标检测/分割等任务精度(附源代码)...

About the priority of Bram IP reset
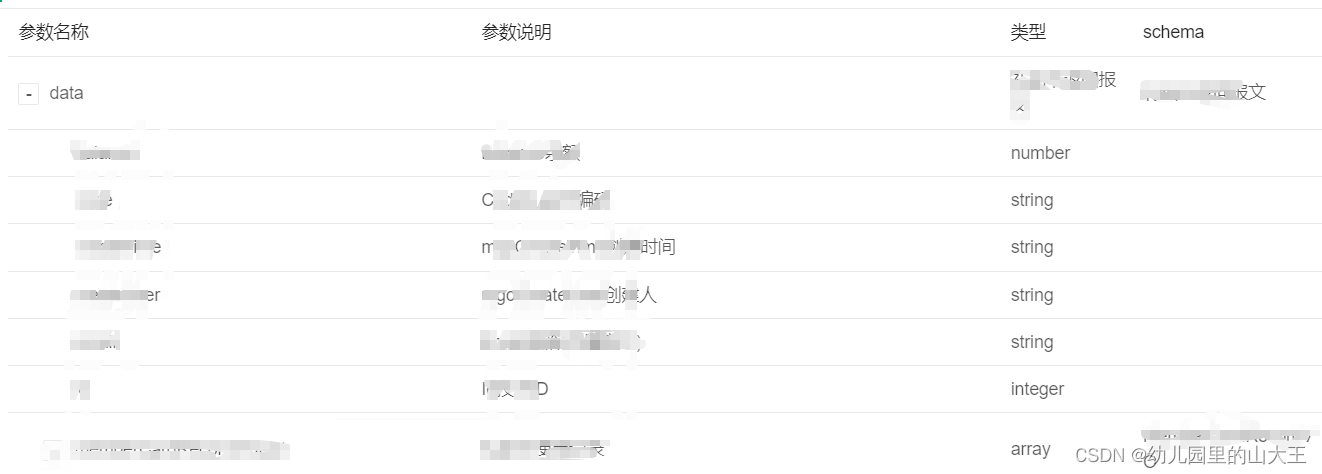
如何形成规范的接口文档
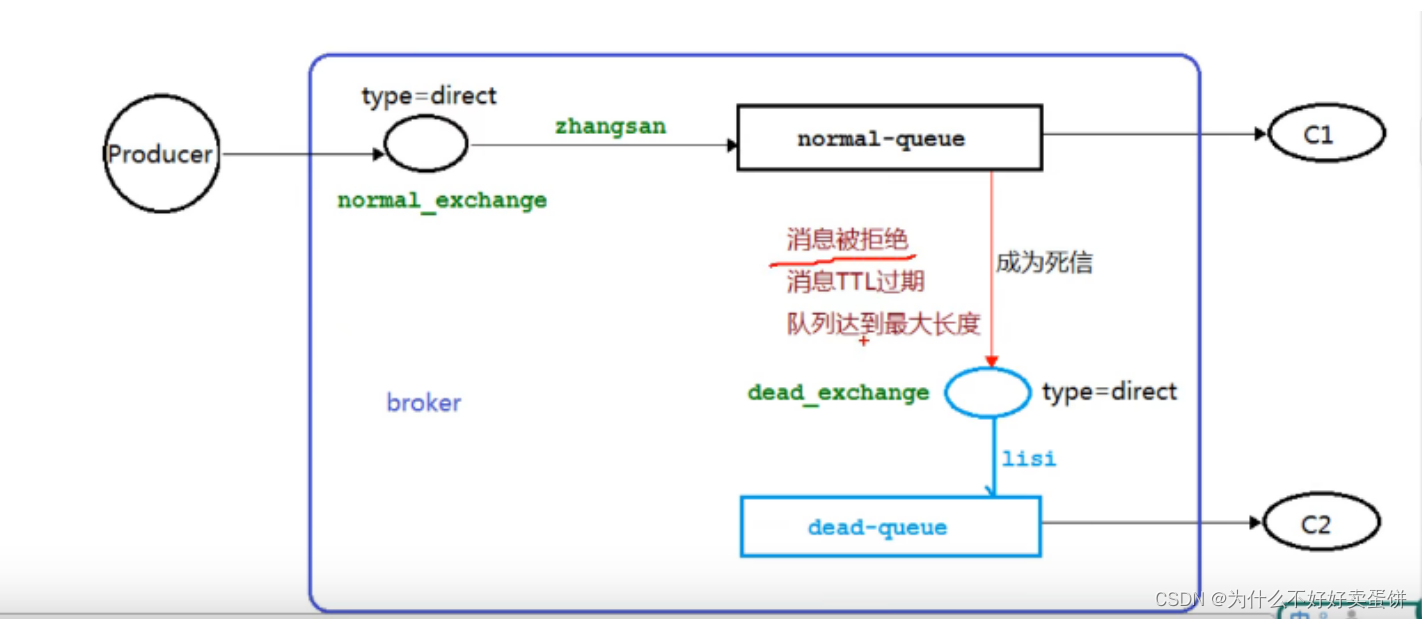
死信队列入门(两个消费者,一个生产者)
Scala基础【HelloWorld代码解析,变量和标识符】
随机推荐
处理文件和目录名
走入并行的世界
CTF reverse Foundation
信息学奥赛一本通 1339:【例3-4】求后序遍历 | 洛谷 P1827 [USACO3.4] 美国血统 American Heritage
Wechat applet regular expression extraction link
全国爱眼教育大会,2022第四届北京国际青少年眼健康产业展会
Leetcode (347) - top k high frequency elements
When JS method passes long type ID value, precision loss will occur
什么是pyc文件
鸿蒙os第四次学习
Leetcode (695) - the largest area of an island
Cocos2d-x项目总结中的一些遇到的问题
About the priority of Bram IP reset
C language OJ gets PE, OJ of ACM introduction~
Leetcode brush questions: binary tree 11 (balanced binary tree)
sun.misc.BASE64Encoder报错解决方法[通俗易懂]
Relationship between mongodb documents
Ros2 topic [01]: installing ros2 on win10
【愚公系列】2022年7月 Go教学课程 004-Go代码注释
插值查找的简单理解