当前位置:网站首页>Leetcode (347) - top k high frequency elements
Leetcode (347) - top k high frequency elements
2022-07-05 20:19:00 【SmileGuy17】
Leetcode(347)—— front K High frequency elements
subject
Answer key
Method 1 : Bucket sort
Ideas
seeing the name of a thing one thinks of its function , Bucket sorting means setting up a bucket for each value , Record the number of occurrences of this value in the bucket ( Or other properties ), Then sort the buckets . For the example , We first get three barrels by sorting them [1,2,3,4], Their values are [4,2,1,1], Indicates the number of times each number appears .
Then , We sort the frequency of barrels , front k A big bucket is the front k A frequent number . Here we can use various sorting algorithms , You can even sort buckets again , Put each old barrel in a different new barrel according to the frequency . For the example , Because the biggest frequency at present is 4, We set up [1,2,3,4] Four new barrels , The old barrels they put into are [[3,4],[2],[],[1]], Indicates the frequency of different numbers . Last , Let's go back and forth , Until I find k Old barrels .
Code implementation
my :
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
if(nums.size() == 1) return nums;
unordered_map<int, int> times;
int maxcount = 0;
for(auto& it: nums) maxcount = max(maxcount, ++times[it]);
vector<vector<int>> bucket(maxcount+1);
for(auto& it: times) bucket[it.second].push_back(it.first);
vector<int> ans;
// Because the answer is guaranteed to be unique , So don't consider maxcount Size
while(k > 0){
if(!bucket[maxcount].empty()){
k -= bucket[maxcount].size();
ans.insert(ans.end(), bucket[maxcount].begin(), bucket[maxcount].end());
}
maxcount--;
}
return ans;
}
};
Complexity analysis
Time complexity : O ( n ) O(n) O(n), among n n n It's array length
Spatial complexity : O ( m a x ( n , k ) ) O(max(n, k)) O(max(n,k)), among n n n It's array length
Method 2 : Heap sort
Ideas
First, traverse the entire array , And use a hash table to record the number of occurrences of each number , And form a 「 Number of occurrences array 」. Find the front of the original array k k k High frequency elements , It's equivalent to finding out 「 Number of occurrences array 」 Before k k k Big value .
The simplest thing to do is to give 「 Number of occurrences array 」 Sort . But because there may be O ( N ) O(N) O(N) A different number of occurrences ( among N N N Is the length of the original array ), Therefore, the overall algorithm complexity will reach O ( N log N ) O(N\log N) O(NlogN), Does not meet the requirements of the topic .
ad locum , We can use the idea of heap : Build a small top pile , Then traverse 「 Number of occurrences array 」:
- If the number of elements in the heap is less than k k k, You can insert it directly into the heap .
- If the number of elements in the heap is equal to k k k, Then check the size of the heap top and the current occurrence times . If the top of the pile is larger , It means at least k k k The number of occurrences is greater than the current value , Therefore, the current value is discarded ; otherwise , Just pop out of the top of the pile , Insert the current value into the heap .
After traversal , The elements in the heap represent 「 Number of occurrences array 」 Middle front k k k Big value .
Code implementation
Leetcode Official explanation :
class Solution {
public:
static bool cmp(pair<int, int>& m, pair<int, int>& n) {
return m.second > n.second;
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> occurrences;
for (auto& v : nums) {
occurrences[v]++;
}
// pair The first element of represents the value of the array , The second element represents the number of times the value appears
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(&cmp)> q(cmp);
for (auto& [num, count] : occurrences) {
if (q.size() == k) {
if (q.top().second < count) {
q.pop();
q.emplace(num, count);
}
} else {
q.emplace(num, count);
}
}
vector<int> ret;
while (!q.empty()) {
ret.emplace_back(q.top().first);
q.pop();
}
return ret;
}
};
Complexity analysis
Time complexity : O ( N log k ) O(N\log k) O(Nlogk), among N N N Is the length of the array . Let's first traverse the original array , And use a hash table to record the number of occurrences , Each element needs O ( 1 ) O(1) O(1) Time for , Common demand O ( N ) O(N) O(N) Time for . And then , We traverse 「 Number of occurrences array 」, Because the size of the heap is at most k k k, Therefore, each heap operation requires O ( log k ) O(\log k) O(logk) Time for , Common demand O ( N log k ) O(N\log k) O(Nlogk) Time for . The sum of the two is O ( N log k ) O(N\log k) O(Nlogk).
Spatial complexity : O ( N ) O(N) O(N). The size of the hash table is O ( N ) O(N) O(N), The size of the heap is O ( k ) O(k) O(k), The total is O ( N ) O(N) O(N).
Method 3 :( The improved ) Quick sort —— That is, quick selection and sorting
Ideas
We can use a fast selection algorithm , Find out 「 Number of occurrences array 」 Before k k k Big value .
First we use arr \textit{arr} arr The array stores the number of occurrences corresponding to each number , Then traverse the array to get the number of occurrences . Then on arr \textit{arr} arr Array for quick sorting .
On the array arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] In the process of quick sorting , We first divide the array into two parts arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] And arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j], And make arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] Each value in does not exceed arr [ q ] \textit{arr}[q] arr[q], And arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j] Each value in is greater than arr [ q ] \textit{arr}[q] arr[q].
therefore , We according to the k k k And the left sub array arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] The length of ( by q − i q q-iq q−iq) The size of the relationship :
- If k ≤ q − i k \le q-i k≤q−i, The array arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] front k k k Big value , Is equal to a subarray arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] front k k k Big value .
- otherwise , Array arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] front k k k Big value , It's equal to all the elements of the left sub array , Add the right sub array arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j] Middle front k − ( q − i ) k - (q - i) k−(q−i) Big value .
The average time complexity of the original quick sort algorithm is O ( N log N ) O(N\log N) O(NlogN). In our algorithm , Just recurse on one branch at a time , Therefore, the average time complexity of the algorithm is reduced to O ( N ) O(N) O(N).
Code implementation
Leetcode Official explanation :
class Solution {
public:
void qsort(vector<pair<int, int>>& v, int start, int end, vector<int>& ret, int k) {
int picked = rand() % (end - start + 1) + start;
swap(v[picked], v[start]);
int pivot = v[start].second;
int index = start;
for (int i = start + 1; i <= end; i++) {
if (v[i].second >= pivot) {
swap(v[index + 1], v[i]);
index++;
}
}
swap(v[start], v[index]);
if (k <= index - start) {
qsort(v, start, index - 1, ret, k);
} else {
for (int i = start; i <= index; i++) {
ret.push_back(v[i].first);
}
if (k > index - start + 1) {
qsort(v, index + 1, end, ret, k - (index - start + 1));
}
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> occurrences;
for (auto& v: nums) {
occurrences[v]++;
}
vector<pair<int, int>> values;
for (auto& kv: occurrences) {
values.push_back(kv);
}
vector<int> ret;
qsort(values, 0, values.size() - 1, ret, k);
return ret;
}
};
Complexity analysis
Time complexity :
among N N N Is the length of the array . Set the processing length to N N N The time complexity of the array is f ( N ) f(N) f(N). Because the process of processing includes one traversal and one recursion of sub branches , At best , Yes f ( N ) = O ( N ) + f ( N / 2 ) f(N) = O(N) + f(N/2) f(N)=O(N)+f(N/2), According to the main theorem , Can get f ( N ) = O ( N ) f(N) = O(N) f(N)=O(N).
In the worst case , Each pivot is located at both ends of the array , Time complexity degenerates to O ( N 2 ) O(N^2) O(N2). But because we randomly select the central element at the beginning of each recursion , So the probability of the worst case is very low .
On average , The time complexity is O ( N ) O(N) O(N).
Spatial complexity : O ( N ) O(N) O(N). The size of hash table is O ( N ) O(N) O(N), The size of the auxiliary array used for sorting is also O ( N ) O(N) O(N), The best space complexity of quick sort is O ( log N ) O(\log N) O(logN), The worst case scenario is O ( N ) O(N) O(N)
边栏推荐
- Flume series: interceptor filtering data
- js实现禁止网页缩放(Ctrl+鼠标、+、-缩放有效亲测)
- Go language | 02 for loop and the use of common functions
- 港股将迎“最牛十元店“,名创优品能借IPO突围?
- Scala基础【HelloWorld代码解析,变量和标识符】
- 中金财富在网上开户安全吗?
- leetcode刷题:二叉树17(从中序与后序遍历序列构造二叉树)
- Is it safe for CICC fortune to open an account online?
- B站UP搭建世界首个纯红石神经网络、基于深度学习动作识别的色情检测、陈天奇《机器学编译MLC》课程进展、AI前沿论文 | ShowMeAI资讯日报 #07.05
- Oracle-表空间管理
猜你喜欢
![[quick start of Digital IC Verification] 3. Introduction to the whole process of Digital IC Design](/img/92/7af0db21b3d7892bdc5dce50ca332e.png)
[quick start of Digital IC Verification] 3. Introduction to the whole process of Digital IC Design

kubernetes资源对象介绍及常用命令(五)-(ConfigMap&Secret)

鸿蒙系统控制LED的实现方法之经典
![[Yugong series] go teaching course in July 2022 004 go code Notes](/img/18/ffbab0a251dc2b78eb09ce281c2703.png)
[Yugong series] go teaching course in July 2022 004 go code Notes
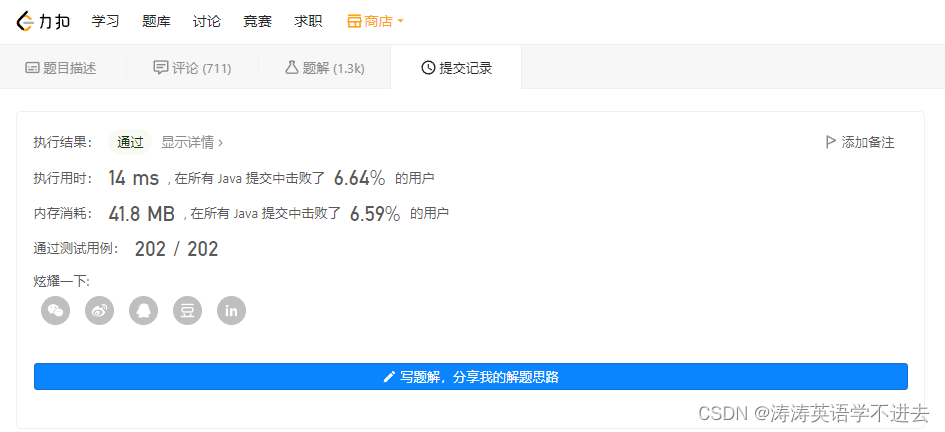
Leetcode skimming: binary tree 17 (construct binary tree from middle order and post order traversal sequence)
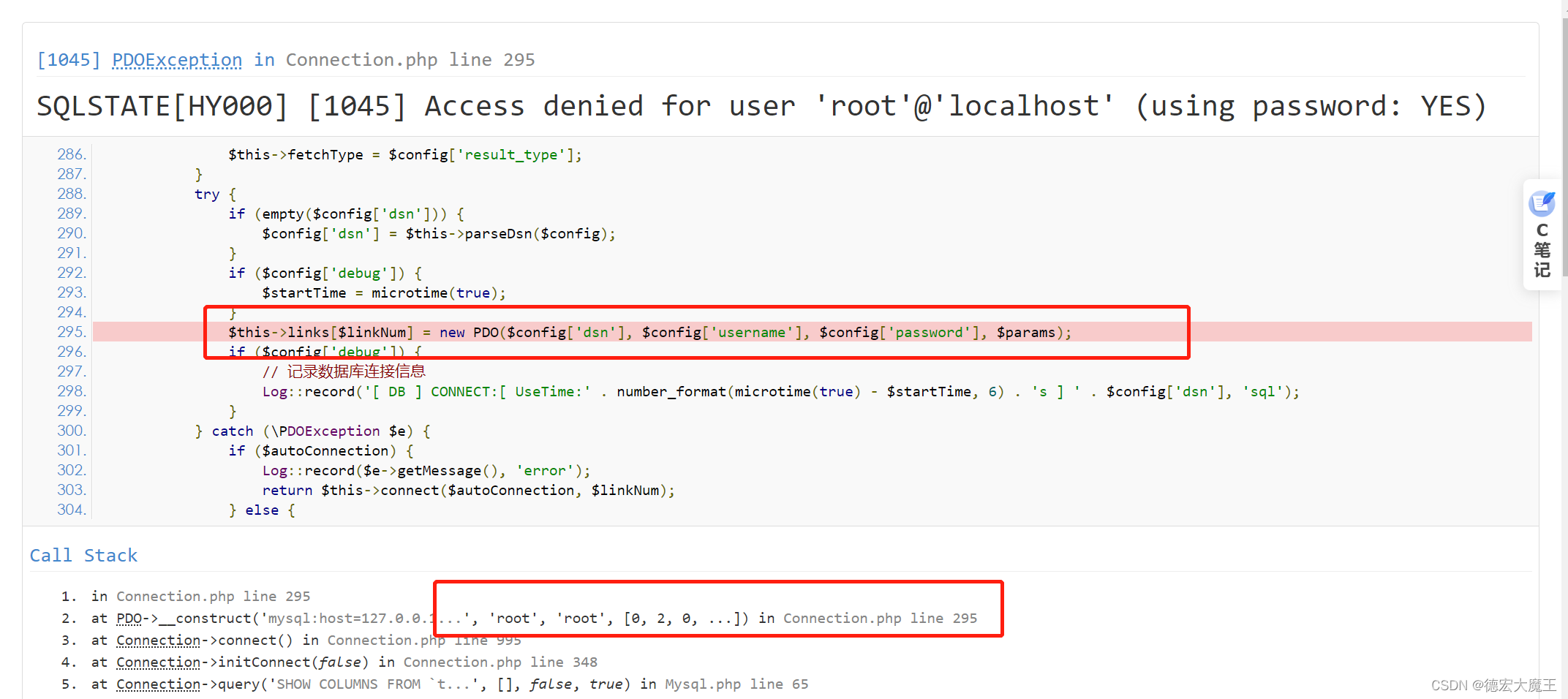
Solve the problem that the database configuration information under the ThinkPHP framework application directory is still connected by default after modification
PyTorch 1.12发布,正式支持苹果M1芯片GPU加速,修复众多Bug

Oracle-表空间管理
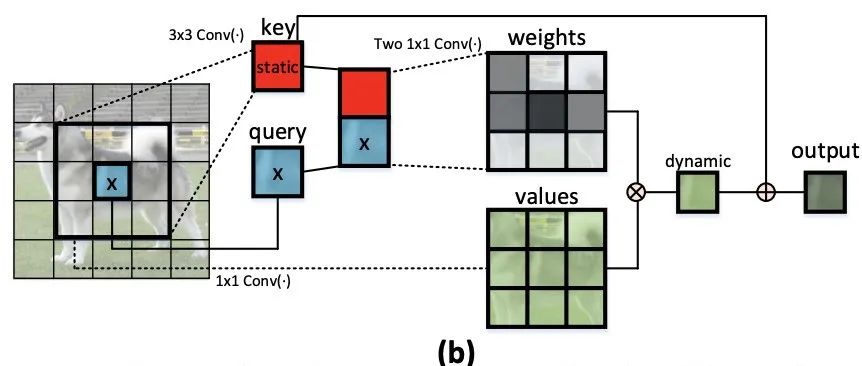
无卷积骨干网络:金字塔Transformer,提升目标检测/分割等任务精度(附源代码)...
How to select the Block Editor? Impression notes verse, notation, flowus
随机推荐
Station B up builds the world's first pure red stone neural network, pornographic detection based on deep learning action recognition, Chen Tianqi's course progress of machine science compilation MLC,
document方法
【c语言】归并排序
Practical demonstration: how can the production research team efficiently build the requirements workflow?
How to select the Block Editor? Impression notes verse, notation, flowus
2022年7月4日-2022年7月10日(ue4视频教程mysql)
[quick start of Digital IC Verification] 1. Talk about Digital IC Verification, understand the contents of the column, and clarify the learning objectives
【数字IC验证快速入门】6、Questasim 快速上手使用(以全加器设计与验证为例)
USACO3.4 “破锣摇滚”乐队 Raucous Rockers - DP
Go language | 03 array, pointer, slice usage
Enter the parallel world
Is it safe for CICC fortune to open an account online?
A solution to PHP's inability to convert strings into JSON
CVPR 2022 | 常见3D损坏和数据增强
leetcode刷题:二叉树18(最大二叉树)
[Yugong series] go teaching course in July 2022 004 go code Notes
物联网智能家居基本方法实现之经典
About the priority of Bram IP reset
[quick start to digital IC Verification] 8. Typical circuits in digital ICs and their corresponding Verilog description methods
走入并行的世界