当前位置:网站首页>L'information et l'entropie, tout ce que vous voulez savoir est ici.
L'information et l'entropie, tout ce que vous voulez savoir est ici.
2022-07-05 09:04:00 【Aelum】
️ Cet article est tiré de [d2l] Information Theory
Si cet article vous aide,On peut se concentrer.️ + - Oui. + Collection + Laissez un message,Votre soutien sera la plus grande force motrice de ma création
En outre,Ce qui est mentionné ici log ( ⋅ ) \log(\cdot) log(⋅) Sauf indication contraire log 2 ( ⋅ ) \log_2(\cdot) log2(⋅).
Table des matières
Un.、De l'information(Self-information)
Prenons un exemple.. Rouler un dé de texture uniforme ,Oui. 6 6 6 Résultats possibles , Et la probabilité que chaque résultat se produise est 1 / 6 1/6 1/6.Maintenant:
- Définir l'événement X = { Le nombre de points n'est pas supérieur à 6 } X=\{\text{ Le nombre de points n'est pas supérieur à }6\} X={ Le nombre de points n'est pas supérieur à 6},Et apparemment, P ( X ) = 1 \mathbb{P}(X)=1 P(X)=1;En outre,C'est des conneries, Ça ne nous dit rien. , Parce que le nombre de points que vous obtenez en lançant un dé ne dépassera certainement pas 6 6 6;
- Définir l'événement X = { Le nombre de points n'est pas supérieur à 5 } X=\{\text{ Le nombre de points n'est pas supérieur à }5\} X={ Le nombre de points n'est pas supérieur à 5},Et apparemment, P ( X ) = 5 / 6 \mathbb{P}(X)=5/6 P(X)=5/6;En outre, Cette phrase contient des informations ,Mais pas beaucoup., Parce que nous pouvons presque deviner le résultat ;
- Définir l'événement X = { Le nombre de points est exactement égal à 2 } X=\{\text{ Le nombre de points est exactement égal à }2\} X={ Le nombre de points est exactement égal à 2},Et apparemment, P ( X ) = 1 / 6 \mathbb{P}(X)=1/6 P(X)=1/6;En outre, Cette phrase est plus informative que celle ci - dessus. ,Parce que { Le nombre de points est exactement égal à 2 } \{\text{ Le nombre de points est exactement égal à }2\} { Le nombre de points est exactement égal à 2} Inclus { Le nombre de points n'est pas supérieur à 5 } \{\text{ Le nombre de points n'est pas supérieur à }5\} { Le nombre de points n'est pas supérieur à 5} Le message est là. .
Comme le montre cet exemple,Un événement X X X La quantité d'information contenue est liée à la probabilité qu'elle se produise. . Plus la probabilité est faible, plus la quantité d'information est grande. , Plus la probabilité est élevée, moins la quantité d'information est importante. .
Définir l'événement X X X La quantité d'informations contenues est I ( X ) I(X) I(X), La probabilité qu'il se produise est p ≜ P ( X ) p\triangleq \mathbb{P}(X) p≜P(X), Comment trouver I ( X ) I(X) I(X) Avec p p p Et la relation entre?
Tout d'abord,, Nous avons le bon sens suivant :
- Observez un Presque Quantité d'information obtenue à partir d'un événement déterminé Presque- Oui. 0 0 0;
- Quantité d'information obtenue par observation conjointe de deux variables aléatoires Pas plus de La quantité d'information obtenue en observant deux variables aléatoires Et, Et l'inégalité est égale si et seulement si deux variables aléatoires Indépendant les uns des autres.
Définir l'événement X = { A Avec B Même chose. Heure Les cheveux. Non. , Le Moyenne A 、 B Phase L'autre Seul Debout } X=\{AAvecBSimultanément,Parmi euxA、BIndépendant les uns des autres\} X={ AAvecBMême chose.HeureLes cheveux.Non.,LeMoyenneA、BPhaseL'autreSeulDebout},Et apparemment, P ( X ) = P ( A ) P ( B ) \mathbb{P}(X)=\mathbb{P}(A)\mathbb{P}(B) P(X)=P(A)P(B), Et selon le bon sens ,Encore. I ( X ) = I ( A ) + I ( B ) I(X)=I(A)+I(B) I(X)=I(A)+I(B).Peut - être. I ( ∗ ) = f ( P ( ∗ ) ) I(*)=f(\mathbb{P}(*)) I(∗)=f(P(∗)),Et
f ( P ( A ) ⋅ P ( B ) ) = f ( P ( X ) ) = I ( X ) = I ( A ) + I ( B ) = f ( P ( A ) ) + f ( P ( B ) ) f(\mathbb{P}(A)\cdot \mathbb{P}(B))=f(\mathbb{P}(X))=I(X)=I(A)+I(B)=f(\mathbb{P}(A))+f(\mathbb{P}(B)) f(P(A)⋅P(B))=f(P(X))=I(X)=I(A)+I(B)=f(P(A))+f(P(B))
C'est facile à voir. log ( ⋅ ) \log(\cdot) log(⋅) Capable de répondre à cette exigence .Mais étant donné que log x \log x logx In ( 0 , 1 ] (0,1] (0,1] Non positif et incrémental monotone ,C'est pourquoi nous utilisons généralement − log ( ⋅ ) -\log(\cdot) −log(⋅) Pour mesurer la quantité d'information sur un événement .
Total ci - dessus,Mise en placeÉvénements X X X La probabilité d'occurrence est p p p, La quantité d'information (Aussi connu sous le nom deDe l'information)Ça peut être calculé comme ça.:
I ( X ) = − log p (1) \textcolor{red}{I(X)=-\log p\tag{1}} I(X)=−logp(1)
- Quand ( 1 ) (1) (1) Où log \log log Par 2 2 2 En bas, L'Unit é d'auto - information est bit \text{bit} bit;
- Quand ( 1 ) (1) (1) Où log \log log Par e e e En bas, L'Unit é d'auto - information est nat \text{nat} nat;
- Quand ( 1 ) (1) (1) Où log \log log Par 10 10 10 En bas, L'Unit é d'auto - information est hart \text{hart} hart.
Je peux l'avoir.:
1 nat = log 2 e bit ≈ 1.443 bit , 1 hart = log 2 10 bit ≈ 3.322 bit 1\;\text{nat}=\log_2 e\;\text{bit}\approx 1.443 \;\text{bit},\quad 1\;\text{hart}=\log_2 10\;\text{bit}\approx 3.322 \;\text{bit} 1nat=log2ebit≈1.443bit,1hart=log210bit≈3.322bit
Nous savons que,Pour toute longueur n n n Séquence binaire de,Il contient: n n n Le message de bits.Par exemple,Pour la séquence 0010 0010 0010, La probabilité qu'il se produise est 1 / 2 4 1/2^4 1/24,Donc,
I ( “ 0010 ” ) = − log 1 2 4 = 4 bits I(\text{“\,0010\,”})=-\log\frac{1}{2^4}=4\;\text{bits} I(“0010”)=−log241=4bits
2.、Entropie(Entropy)
Mise en placeVariables aléatoires X X X Obéir à la distribution D \mathcal{D} D,Et X X X L'entropie est définie comme l'attente de sa quantité d'information :
H ( X ) = E X ∼ D [ I ( X ) ] (2) \textcolor{red}{H(X)=\mathbb{E}_{X\sim\mathcal{D}}[I(X)]}\tag{2} H(X)=EX∼D[I(X)](2)
Si X X X Est une distribution discrète ,Et
H ( X ) = − E X ∼ D [ log p i ] = − ∑ i p i log p i H(X)=-\mathbb{E}_{X\sim\mathcal{D}}[\log p_i]=-\sum_ip_i\log p_i H(X)=−EX∼D[logpi]=−i∑pilogpi
Si X X X Est une distribution continue ,Et
H ( X ) = − E X ∼ D [ log p ( x ) ] = − ∫ p ( x ) log p ( x ) d x H(X)=-\mathbb{E}_{X\sim\mathcal{D}}[\log p(x)]=-\int p(x)\log p(x)\text{d}x H(X)=−EX∼D[logp(x)]=−∫p(x)logp(x)dx
Dans des situations discrètes ,Mise en place X X X Prends juste k k k Valeurs,Oui.: 0 ≤ H ( X ) ≤ log k 0\leq H(X)\leq \log k 0≤H(X)≤logk.
Contrairement à la quantité d'information ,Ici. X X X Est une variable aléatoire, pas un événement
Voir les événements comme un point , La quantité d'information peut être considérée comme l'information générée par un point , L'entropie de l'information représente la quantité moyenne d'information générée par une série de points.
Dans les chapitres suivants, nous ne parlerons que de cas discrets. , Formule de raisonnement analogique dans le cas continu
2.1 Entropie conjointe(Joint Entropy)
Nous savons déjà comment calculer X X X Entropie de l'information ,Comment calculer ( X , Y ) (X,Y) (X,Y) Et l'entropie de l'information ?
Mise en place ( X , Y ) ∼ D (X,Y)\sim\mathcal{D} (X,Y)∼D, La distribution de probabilité conjointe est p i j ≜ P ( X = x i , Y = y j ) p_{ij}\triangleq \mathbb{P}(X=x_i,Y=y_j) pij≜P(X=xi,Y=yj),Rappelle - toi. p i = P ( X = x i ) , p j = P ( Y = y j ) p_i=\mathbb{P}(X=x_i),\,p_j=\mathbb{P}(Y=y_j) pi=P(X=xi),pj=P(Y=yj), Similaire à la définition de l'entropie de l'information
H ( X , Y ) = − ∑ i j p i j log p i j (3) \textcolor{red}{H(X,Y)=-\sum_{ij}p_{ij}\log p_{ij}}\tag{3} H(X,Y)=−ij∑pijlogpij(3)
Si X = Y X=Y X=Y,Et H ( X , Y ) = H ( X ) = H ( Y ) H(X,Y)=H(X)=H(Y) H(X,Y)=H(X)=H(Y);Si X X X Et Y Y Y Indépendant les uns des autres,Et p i j = p i ⋅ p j p_{ij}=p_i\cdot p_j pij=pi⋅pj,Et puis
H ( X , Y ) = − ∑ i j ( p i ⋅ p j ) ( log p i + log p j ) = − ∑ j p j ∑ i p i log p i − ∑ i p i ∑ j p j log p j = H ( X ) + H ( Y ) H(X,Y)=-\sum_{ij}(p_i\cdot p_j)(\log p_i+\log p_j)=-\sum_j p_j\sum_i p_i\log p_i-\sum_ip_i\sum_jp_j\log p_j=H(X)+H(Y) H(X,Y)=−ij∑(pi⋅pj)(logpi+logpj)=−j∑pji∑pilogpi−i∑pij∑pjlogpj=H(X)+H(Y)
En outre, Il y a toujours une inégalité :
H ( X ) , H ( Y ) ≤ H ( X , Y ) ≤ H ( X ) + H ( Y ) H(X),H(Y)\leq H(X,Y)\leq H(X)+H(Y) H(X),H(Y)≤H(X,Y)≤H(X)+H(Y)
2.2 Entropie conditionnelle(Conditional Entropy)
Entropie conditionnelle H ( Y ∣ X ) H(Y|X) H(Y∣X) Représente une variable aléatoire connue X X X Variable aléatoire dans le cas de Y Y Y Incertitude,Défini comme suit: X X X Dans des conditions données Y Y Y La paire d'entropie de la distribution de probabilité conditionnelle de X X X Attentes mathématiques:
H ( Y ∣ X ) = ∑ i p i H ( Y ∣ X = x i ) = ∑ i p i ( − ∑ j p j ∣ i log p j ∣ i ) = − ∑ i j p i j log p j ∣ i (4) H(Y|X)=\sum_i p_iH(Y|X=x_i)=\sum_i p_i \left( -\sum_j p_{j|i}\log p_{j|i}\right)=-\sum_{ij}p_{ij}\log p_{j|i}\tag{4} H(Y∣X)=i∑piH(Y∣X=xi)=i∑pi(−j∑pj∣ilogpj∣i)=−ij∑pijlogpj∣i(4)
Utilisation p j ∣ i = p i j / p i p_{j|i}=p_{ij}/p_i pj∣i=pij/pi Oui.
H ( Y ∣ X ) = H ( X , Y ) − H ( X ) H(Y|X)=H(X,Y)-H(X) H(Y∣X)=H(X,Y)−H(X)
Comme le montre la formule ci - dessus,, H ( Y ∣ X ) H(Y|X) H(Y∣X) Représente en fait une Y Y Y Mais non inclus dans X X X Information in(Similaire à P ( B \ A ) = P ( A ∪ B ) − P ( A ) \mathbb{P}(B\backslash A)=\mathbb{P}(A\cup B)-\mathbb{P}(A) P(B\A)=P(A∪B)−P(A)).
2.3 Information mutuelle(Mutual Information)
Compte tenu deVariables aléatoires ( X , Y ) (X,Y) (X,Y),On le sait déjà. X X X Les informations peuvent être utilisées H ( X ) H(X) H(X) Pour représenter; ( X , Y ) (X,Y) (X,Y) Le total des informations disponibles H ( X , Y ) H(X,Y) H(X,Y) Pour représenter;Inclus dans Y Y Y Mais non inclus dans X X X Les informations contenues dans H ( Y ∣ X ) H(Y|X) H(Y∣X) Pour représenter. Que devons - nous mesurer? X X X Et Y Y Y Qu'en est - il des informations qu'ils contiennent? ?
La réponse est:Information mutuelle,Il est défini comme suit:(Peut être compris comme une collection X X X Avec Y Y Y Intersection de):
I ( X , Y ) = H ( X , Y ) − H ( Y ∣ X ) − H ( X ∣ Y ) (5) \textcolor{red}{I(X,Y)=H(X,Y)-H(Y|X)-H(X|Y)}\tag{5} I(X,Y)=H(X,Y)−H(Y∣X)−H(X∣Y)(5)
Entropie、Entropie conjointe、Entropie conditionnelle、 La relation entre les informations mutuelles est la suivante: :
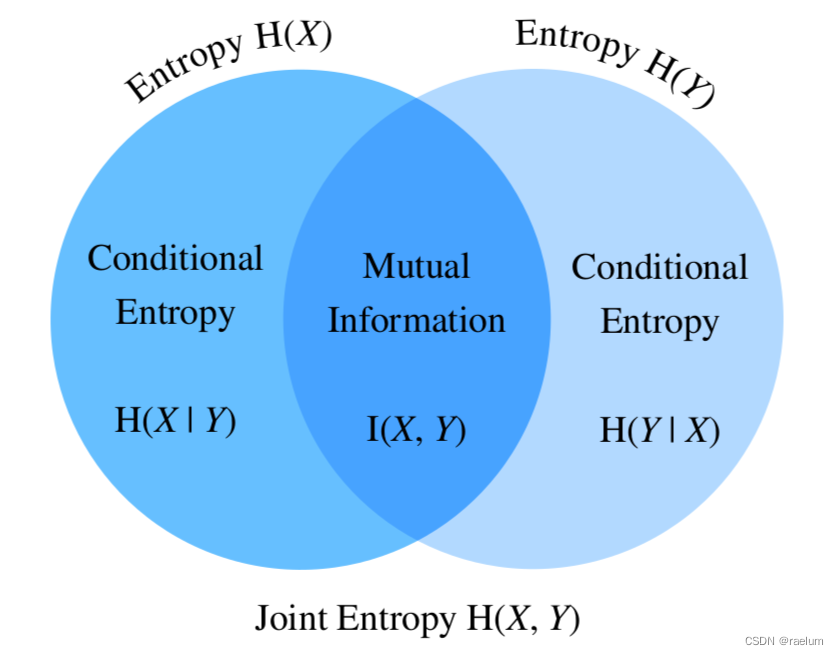
On peut aussi le voir sur la photo ci - dessus. :
I ( X , Y ) = H ( X ) − H ( X ∣ Y ) I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) \begin{aligned} I(X,Y)&=H(X)-H(X|Y) \\ I(X,Y)&=H(Y)-H(Y|X) \\ I(X,Y)&=H(X)+H(Y)-H(X,Y) \end{aligned} I(X,Y)I(X,Y)I(X,Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)
On va ( 5 ) (5) (5) Expansion de l'équation
I ( X , Y ) = − ∑ i j p i j log p i j + ∑ i j p i j log p j ∣ i + ∑ i j p i j log p i ∣ j = ∑ i j p i j ( log p j ∣ i + log p i ∣ j − log p i j ) = ∑ i j p i j log p i j p i ⋅ p j = E ( X , Y ) ∼ D [ log p i j p i ⋅ p j ] \begin{aligned} I(X,Y)&=-\sum_{ij}p_{ij}\log p_{ij}+\sum_{ij}p_{ij}\log p_{j|i}+\sum_{ij}p_{ij}\log p_{i|j} \\ &=\sum_{ij}p_{ij}(\log p_{j|i}+\log p_{i|j}-\log p_{ij}) \\ &=\sum_{ij} p_{ij} \log \frac{p_{ij}}{p_i\cdot p_j} \\ &=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\left[\log \frac{p_{ij}}{p_i\cdot p_j}\right] \end{aligned} I(X,Y)=−ij∑pijlogpij+ij∑pijlogpj∣i+ij∑pijlogpi∣j=ij∑pij(logpj∣i+logpi∣j−logpij)=ij∑pijlogpi⋅pjpij=E(X,Y)∼D[logpi⋅pjpij]
Quelques propriétés de l'information mutuelle :
- Symétrie: I ( X , Y ) = I ( Y , X ) I(X,Y)=I(Y,X) I(X,Y)=I(Y,X);
- Non négatif: I ( X , Y ) ≥ 0 I(X,Y)\geq 0 I(X,Y)≥0;
- I ( X , Y ) = 0 I(X,Y)=0 I(X,Y)=0 ⇔ \;\Leftrightarrow\; ⇔ X X X Avec Y Y Y Indépendant les uns des autres;
2.4 Information mutuelle ponctuelle(Pointwise Mutual Information)
L'information mutuelle ponctuelle est définie comme suit: :
PMI ( x i , y j ) = log p i j p i ⋅ p j (6) \textcolor{red}{\text{PMI}(x_i,y_j)=\log \frac{p_{ij}}{p_i\cdot p_j}} \tag{6} PMI(xi,yj)=logpi⋅pjpij(6)
Union 2.3 Section, Nous découvrirons qu'il y a une relation ( Tout comme l'entropie de l'information est l'attente de la quantité d'information , L'information mutuelle est également l'attente de l'information mutuelle ponctuelle )
I ( X , Y ) = E ( X , Y ) ∼ D [ PMI ( x i , y j ) ] I(X,Y)=\mathbb{E}_{(X,Y)\sim \mathcal{D}}\left[\text{PMI}(x_i,y_j)\right] I(X,Y)=E(X,Y)∼D[PMI(xi,yj)]
PMI Plus la valeur est élevée,Représentation x i x_i xi Avec y j y_j yj Plus la corrélation est forte .PMI Souvent utilisé NLP Calculer la corrélation entre deux mots dans une tâche , Mais si le corpus est insuffisant ,Ça pourrait arriver p i j = 0 p_{ij}=0 pij=0 Situation, Cela conduit à l'information mutuelle des deux mots − ∞ -\infty −∞, Une correction est donc nécessaire :
PPMI ( x i , y j ) = max ( 0 , PMI ( x i , y j ) ) \text{PPMI}(x_i,y_j)=\max(0,\text{PMI}(x_i,y_j)) PPMI(xi,yj)=max(0,PMI(xi,yj))
Ce qui précède PPMI Aussi appeléInformation mutuelle ponctuelle(Positive PMI).
Trois、Entropie relative(KLDispersion)
Entropie relative(Relative Entropy)Aussi appeléKLDispersion(Kullback–Leibler divergence), Ce dernier est son nom le plus courant .
Définir des variables aléatoires X X X Suivre la distribution des probabilités P P P, Maintenant nous essayons d'utiliser une autre distribution de probabilité Q Q Q Pour estimer P P P(Hypothèses Y ∼ Q Y\sim Q Y∼Q).Note p i = P ( X = x i ) , q i = P ( Y = x i ) p_i=\mathbb{P}(X=x_i),\,q_i=\mathbb{P}(Y=x_i) pi=P(X=xi),qi=P(Y=xi),EtKL La divergence est définie comme suit:
D KL ( P ∥ Q ) = E X ∼ P [ log p i q i ] = ∑ i p i log p i q i (7) D_{\text{KL}}(P\Vert Q)=\mathbb{E}_{X\sim P}\left[\log \frac{p_i}{q_i}\right]=\sum_ip_i\log \frac{p_i}{q_i}\tag{7} DKL(P∥Q)=EX∼P[logqipi]=i∑pilogqipi(7)
KL Quelques propriétés de divergence :
- Asymétrie: D KL ( P ∥ Q ) ≠ D KL ( Q ∥ P ) D_{\text{KL}}(P\Vert Q)\neq D_{\text{KL}}(Q\Vert P) DKL(P∥Q)=DKL(Q∥P);
- Non négatif: D KL ( P ∥ Q ) ≥ 0 D_{\text{KL}}(P\Vert Q)\geq 0 DKL(P∥Q)≥0, L'équation est vraie si et seulement si P = Q P=Q P=Q;
- S'il existe x i x_i xi De faire p i > 0 , q i = 0 p_i>0,\,q_i=0 pi>0,qi=0,Et D KL ( P ∥ Q ) = ∞ D_{\text{KL}}(P\Vert Q) =\infty DKL(P∥Q)=∞.
KL La divergence est utilisée pour mesurer la différence entre les deux distributions de probabilité. . Si les deux distributions sont exactement égales ,EtKLLa divergence est 0 0 0.Donc,,KL La divergence peut être utilisée comme fonction de perte pour les tâches Multi - catégories .
Parce queKL La divergence ne satisfait pas à la symétrie , Donc ce n'est pas strictement “Distance”
Quatre、Entropie croisée(Cross-Entropy)
On va ( 7 ) (7) (7) Type de démontage
D KL ( P ∥ Q ) = ∑ i p i log p i − ∑ i p i log q i D_{\text{KL}}(P\Vert Q)=\sum_i p_i\log p_i-\sum_i p_i\log q_i DKL(P∥Q)=i∑pilogpi−i∑pilogqi
Si CE ( P , Q ) = − ∑ i p i log q i \text{CE}(P,Q)=-\sum_i p_i\log q_i CE(P,Q)=−∑ipilogqi, Alors la formule ci - dessus peut être écrite comme suit:
D KL ( P ∥ Q ) = CE ( P , Q ) − H ( P ) D_{\text{KL}}(P\Vert Q)=\text{CE}(P,Q)-H(P) DKL(P∥Q)=CE(P,Q)−H(P)
Et CE ( P , Q ) \text{CE}(P,Q) CE(P,Q) C'est ce qu'on dit.Entropie croisée, Il est officiellement défini comme suit:
CE ( P , Q ) = − E X ∼ P [ log q i ] (8) \textcolor{red}{\text{CE}(P,Q)=-\mathbb{E}_{X\sim P}[\log q_i]}\tag{8} CE(P,Q)=−EX∼P[logqi](8)
UnionKLNon - négativité de la divergence,On peut encore l'avoir. CE ( P , Q ) ≥ H ( P ) \text{CE}(P,Q)\geq H(P) CE(P,Q)≥H(P), Cette inégalité est également appelée inégalité Gibbs .
En général CE ( P , Q ) \text{CE}(P,Q) CE(P,Q) Il sera écrit comme suit: H ( P , Q ) H(P,Q) H(P,Q)
Un exemple de calcul de l'entropie croisée :
P P P C'est la vraie distribution. ,Et Q Q Q Est la distribution estimée , Examen de trois questions de classification ,Pour un échantillon, Les résultats réels des étiquettes et des prévisions sont présentés dans le tableau ci - dessous. :
| Catégorie 1 | Catégorie 2 | Catégorie 3 | |
|---|---|---|---|
| target | 0 | 1 | 0 |
| prediction | 0.2 | 0.7 | 0.1 |
Comme le montre le tableau ci - dessus,, L'échantillon appartient à la catégorie 2,Et p 1 = 0 , p 2 = 1 , p 3 = 0 , q 1 = 0.2 , q 2 = 0.7 , q 3 = 0.1 p_1=0,p_2=1,p_3=0,q_1=0.2,q_2=0.7,q_3=0.1 p1=0,p2=1,p3=0,q1=0.2,q2=0.7,q3=0.1.
Donc,
CE ( P , Q ) = − ( 0 ⋅ log 0.2 + 1 ⋅ log 0.7 + 0 ⋅ log 0.1 ) = − log 0.7 ≈ 0.5146 \text{CE}(P,Q)=-(0\cdot \log 0.2+1\cdot \log 0.7+0\cdot \log 0.1)=-\log 0.7\approx 0.5146 CE(P,Q)=−(0⋅log0.2+1⋅log0.7+0⋅log0.1)=−log0.7≈0.5146
Lorsque l'ensemble de données est donné , H ( P ) H(P) H(P) C'est une constante. ,Donc,KL La divergence et l'entropie croisée peuvent être utilisées comme fonctions de perte pour les problèmes de classification multiple . Quand la vraie distribution P P P - Oui. One-Hot Quand un vecteur,Oui. H ( P ) = 0 H(P)=0 H(P)=0, L'entropie croisée est égale à KLDispersion
4.1 Entropie croisée binaire(Binary Cross-Entropy)
Entropie croisée binaire(BCE) Est un cas particulier d'entropie croisée
BCE ( P , Q ) = − ∑ i = 1 2 p i log q i = − ( p 1 log q 1 + p 2 log q 2 ) = − ( p 1 log q 1 + ( 1 − p 1 ) log ( 1 − q 1 ) ) \begin{aligned} \text{BCE}(P,Q)&=-\sum_{i=1}^2p_i\log q_i \\ &=-(p_1\log q_1+p_2\log q_2) \\ &=-(p_1\log q_1+(1-p_1)\log (1-q_1))\qquad \end{aligned} BCE(P,Q)=−i=1∑2pilogqi=−(p1logq1+p2logq2)=−(p1logq1+(1−p1)log(1−q1))
BCE Fonction de perte utilisée comme classification binaire ou Multi - étiquettes .
Généralement connecté avant la perte d'entropie croisée Softmax, La perte d'entropie croisée binaire est habituellement précédée d'une perte d'entropie croisée binaire. Sigmoid
Scénario de classification II , La couche de sortie peut utiliser à la fois un neurone +Sigmoid Deux neurones peuvent également être utilisés +Softmax,Les deux sont équivalents, Mais il est plus rapide de s'entraîner avec le premier
BCE Peut encore passer MLE Je l'ai..Compte tenu de n n n Échantillons: x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn, Étiquette de chaque échantillon y i y_i yi Non 0 0 0 C'est - à - dire: 1 1 1( 1 1 1 Représente la classe positive, 0 0 0 Représente la classe négative), Les paramètres du réseau neuronal sont résumés comme suit: θ \theta θ. Notre objectif est de trouver le meilleur θ \theta θ De faire y ^ i = P θ ( y i ∣ x i ) \hat{y}_i=\mathbb{P}_{\theta}(y_i|x_i) y^i=Pθ(yi∣xi).Mise en place x i x_i xi La probabilité d'être classée comme positive est π i = P θ ( y i = 1 ∣ x i ) \pi_i=\mathbb{P}_{\theta}(y_i=1|x_i) πi=Pθ(yi=1∣xi),La fonction de probabilité logarithmique est
ℓ ( θ ) = log L ( θ ) = log ∏ i = 1 n π i y i ( 1 − π i ) 1 − y i = ∑ i = 1 n y i log π i + ( 1 − y i ) log ( 1 − π i ) \begin{aligned} \ell(\theta)&=\log L(\theta) \\ &=\log \prod_{i=1}^n \pi_i^{y_i}(1-\pi_i)^{1-y_i} \\ &=\sum_{i=1}^ny_i\log \pi_i+(1-y_i)\log (1-\pi_i) \end{aligned} ℓ(θ)=logL(θ)=logi=1∏nπiyi(1−πi)1−yi=i=1∑nyilogπi+(1−yi)log(1−πi)
Maximiser ℓ ( θ ) \ell(\theta) ℓ(θ) Équivalent à la minimisation − ℓ ( θ ) -\ell(\theta) −ℓ(θ), Ce dernier est la perte d'entropie croisée binaire .
Les blogueurs sont peu instruits, S'il y a des erreurs dans cet article, veuillez les signaler dans la section commentaires.
边栏推荐
- Golang foundation -- map, array and slice store different types of data
- Applet (global data sharing)
- Multiple linear regression (sklearn method)
- Codeforces Round #648 (Div. 2) E.Maximum Subsequence Value
- asp.net(c#)的货币格式化
- Ros- learn basic knowledge of 0 ROS - nodes, running ROS nodes, topics, services, etc
- Attention is all you need
- Applet (subcontracting)
- Codeforces round 684 (Div. 2) e - green shopping (line segment tree)
- Meta标签详解
猜你喜欢
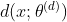
生成对抗网络
![[code practice] [stereo matching series] Classic ad census: (5) scan line optimization](/img/54/cb1373fbe7b21c5383580e8b638a2c.jpg)
[code practice] [stereo matching series] Classic ad census: (5) scan line optimization
Add discount recharge and discount shadow ticket plug-ins to the resource realization applet

Programming implementation of ROS learning 2 publisher node

Halcon snap, get the area and position of coins

Halcon affine transformations to regions
![[code practice] [stereo matching series] Classic ad census: (6) multi step parallax optimization](/img/54/cb1373fbe7b21c5383580e8b638a2c.jpg)
[code practice] [stereo matching series] Classic ad census: (6) multi step parallax optimization

My university

Wechat H5 official account to get openid climbing account
Programming implementation of ROS learning 5-client node
随机推荐
Use and programming method of ros-8 parameters
. Net service governance flow limiting middleware -fireflysoft RateLimit
IT冷知识(更新ing~)
资源变现小程序添加折扣充值和折扣影票插件
编辑器-vi、vim的使用
golang 基础 —— golang 向 mysql 插入的时间数据和本地时间不一致
ECMAScript6介绍及环境搭建
C# LINQ源码分析之Count
深度学习模型与湿实验的结合,有望用于代谢通量分析
2309. 兼具大小写的最好英文字母
Basic number theory -- Euler function
Halcon Chinese character recognition
OpenFeign
Multiple linear regression (sklearn method)
使用arm Neon操作,提高内存拷贝速度
[beauty of algebra] singular value decomposition (SVD) and its application to linear least squares solution ax=b
Array, date, string object method
Wechat H5 official account to get openid climbing account
Introduction Guide to stereo vision (4): DLT direct linear transformation of camera calibration [recommended collection]
np. allclose