当前位置:网站首页>2022牛客多校训练第二场 J题 Link with Arithmetic Progression
2022牛客多校训练第二场 J题 Link with Arithmetic Progression
2022-08-05 00:18:00 【Rain Sure】
题目链接
Link with Arithmetic Progression
题目大意
给定一个数组,让我们找到一条拟合它的直线,要求均方误差最小。相信大家在数学课或者机器学习课上都学过相关的知识。
题解
T a r g e t = m i n ( ∑ i = 1 n [ a 1 + ( i − 1 ) × d − a i ] 2 ) Target = min(\sum^{n}_{i = 1} [a_1 + (i - 1) \times d - a_i]^2) Target=min(i=1∑n[a1+(i−1)×d−ai]2)
这就是我们要求的值,我们需要让其最小,我们可以先考虑把 a 1 a_1 a1求出来,很明显,随着 a 1 a_1 a1从负无穷到正无穷的变化过程中,Target值是先下降后上升的,也就是说 a 1 a_1 a1是一个凹函数,因此我们可以考虑用三分求 a 1 a_1 a1,然后在考虑在 a 1 a_1 a1确定的情况下,如何确定 d d d。
我们对公式进行变形:
= [ a 1 + ( i − 1 ) × d ] 2 − 2 × [ a 1 + ( i − 1 ) × d ] × a i + a i 2 = [a_1 + (i - 1)\times d]^2 - 2 \times [a_1 + (i - 1) \times d] \times a_i + {a_i}^2 =[a1+(i−1)×d]2−2×[a1+(i−1)×d]×ai+ai2
然后,将带有 d d d的合并同类项。
= ( i − 1 ) 2 × d 2 + 2 × ( i − 1 ) × ( a 1 − a i ) × d + a 1 2 + a i 2 = (i - 1) ^2 \times d^2 + 2 \times (i - 1) \times (a_1 - a_i) \times d + {a_1}^2 + {a_i}^2 =(i−1)2×d2+2×(i−1)×(a1−ai)×d+a12+ai2
根据二次函数的知识,我们可以很轻松的确定 d = − b 2 ∗ ( i − 1 ) 2 d = \frac {-b} {2 * (i - 1) ^ 2} d=2∗(i−1)2−b
然后,就可以进行计算了。
话不多说,上代码:
代码
#include<iostream>
#include<cstring>
#include <cstdio>
#include <cctype>
using namespace std;
#define int long long
#define double long double
const int maxn = 100010;
int w[maxn];
int n;
namespace GTI
{
char gc(void)
{
const int S = 1 << 16;
static char buf[S], *s = buf, *t = buf;
if (s == t) t = buf + fread(s = buf, 1, S, stdin);
if (s == t) return EOF;
return *s++;
}
int gti(void)
{
int a = 0, b = 1, c = gc();
for (; !isdigit(c); c = gc()) b ^= (c == '-');
for (; isdigit(c); c = gc()) a = a * 10 + c - '0';
return b ? a : -a;
}
}
using GTI::gti;
double check(double a1)
{
double a = 0, b = 0;
for(int i = 1; i <= n; i ++){
a += (i - 1) * (i - 1);
b += 2 * (i - 1) * (a1 - w[i]);
}
double d = - b / (2 * a);
double res = 0;
for(int i = 1; i <= n; i ++){
res += (a1 + (i - 1) * d - w[i]) * (a1 + (i - 1) * d - w[i]);
}
return res;
}
signed main()
{
int t; t = gti();
while(t --)
{
n = gti();
for(int i = 1; i <= n; i ++) w[i] = gti();
double l = -1e10, r = 1e10;
while(r - l > 1e-5) {
double len = r - l;
double mid_l = l + len / 3, mid_r = r - len / 3;
if(check(mid_l) >= check(mid_r)) l = mid_l;
else r = mid_r;
}
printf("%.10Lf\n", check(r));
}
return 0;
}
边栏推荐
- jenkins send mail system configuration
- [Cloud Native--Kubernetes] Pod Controller
- could not build server_names_hash, you should increase server_names_hash_bucket_size: 32
- gorm联表查询-实战
- Chinese and Japanese color style
- SQL association table update
- DNS常见资源记录类型详解
- Detailed explanation of common DNS resource record types
- 机器学习(公式推导与代码实现)--sklearn机器学习库
- Modelers experience sharing: model study method
猜你喜欢
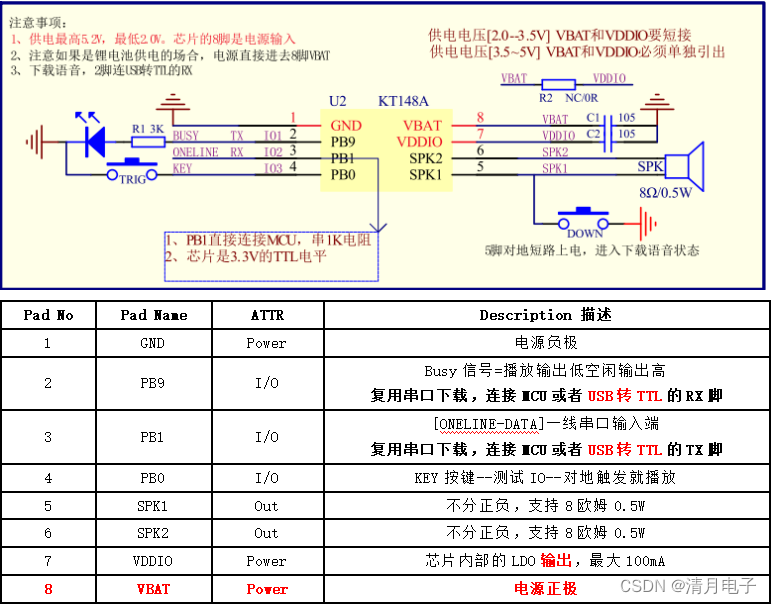
How to burn the KT148A voice chip into the chip through the serial port and the tools on the computer

Three tips for you to successfully get started with 3D modeling

The master teaches you the 3D real-time character production process, the game modeling process sharing

【LeetCode】Summary of Two Pointer Problems
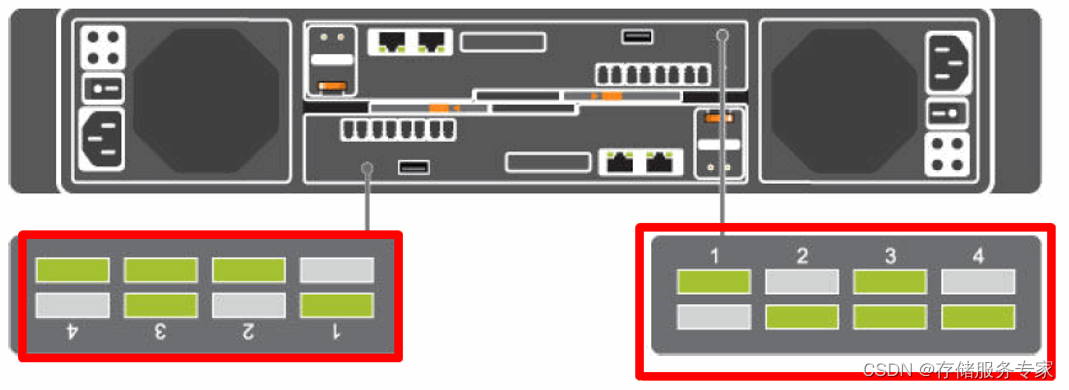
看图识字,DELL SC4020 / SCv2000 控制器更换过程

矩阵数学原理
导入JankStats检测卡帧库遇到问题记录
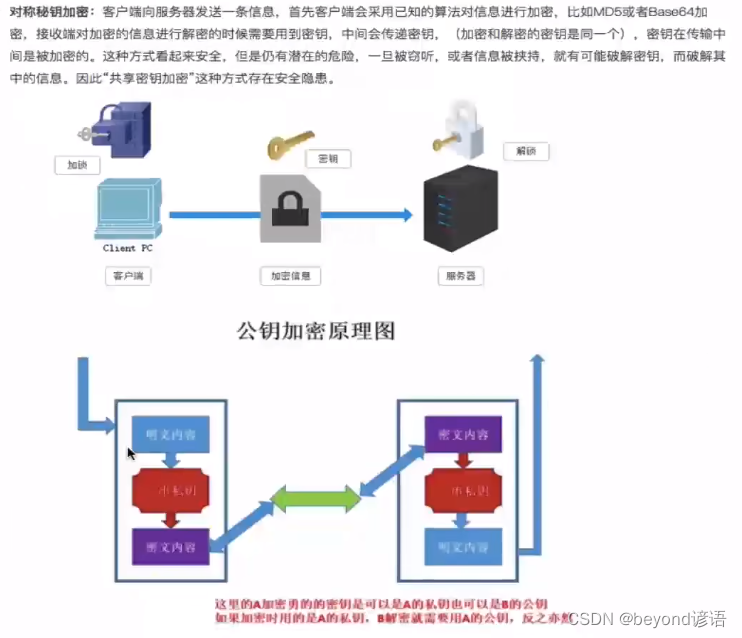
First, the basic concept of reptiles
MAUI Blazor 权限经验分享 (定位,使用相机)

How to automatically push my new articles to my fans (very simple, can't learn to hit me)
随机推荐
LeetCode Hot 100
could not build server_names_hash, you should increase server_names_hash_bucket_size: 32
MongoDB权限验证开启与mongoose数据库配置
.net(C#)获取两个日期间隔的年月日
软件测试面试题:软件验收测试的合格通过准则?
[230]连接Redis后执行命令错误 MISCONF Redis is configured to save RDB snapshots
机器学习(公式推导与代码实现)--sklearn机器学习库
NMS原理及其代码实现
隐私计算综述
工业物联网 —— 新型数据库的召唤
oracle创建用户以后的权限问题
GO中sync包自由控制并发的方法
国内网站用香港服务器会被封吗?
ansible学习笔记分享-含剧本示例
数据类型-整型(C语言)
【Valentine's Day special effects】--Canvas realizes full screen love
《MySQL入门很轻松》第2章:MySQL管理工具介绍
关于使用read table 语句
leetcode经典例题——单词拆分
Mysql based