math_ Derivative function derivation of limit & differential & derivative & derivative / logarithmic function (derivative definition limit method) / derivative formula derivation of exponential functi

differential & derivative & Wechat Business

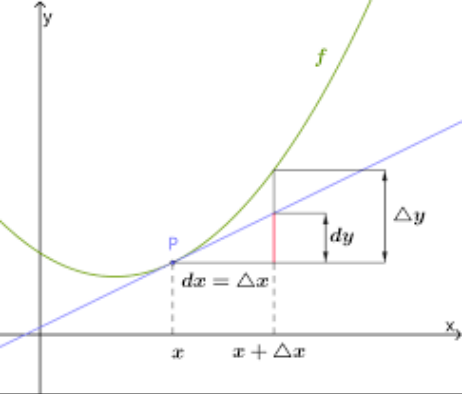
Function in $x=x_0$ Definition of derivative

• Define two points

$$\begin{gathered} A_{x_0}(x_0,f(x_0));(fingersetx=x_{0}It\text{'}s\; aboutOfextremelylimit) \\ {B}_x=(x,f(x))=(x_0+\Delta x,f(x_0+\Delta x)) \\ \{\begin{array}{l}\Delta x=x-x_0\\ \Delta y=\{\begin{array}{l}f(x)-f(x_0)\\ f(x_0+\Delta x)-f(x_0)\end{array}\end{array} \\ x\to x_0*\Delta x\to 0 \\ Yeswhen,alsorememberh=\Delta x \end{gathered}$$

$$\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\{\begin{array}{l}\underset{\Delta x\to 0}{\lim }\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\\ \underset{x\to x_0}{\lim }\frac{f(x)-f(x_0)}{x-x_0}\\ \underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}\end{array}$$

Usually , For the convenience of writing , The third form is often used for derivation :
$$f^{\prime }(x_0)=\underset{h\to 0}{\lim }\frac{f(x_0+h)-f(x_0)}{h}$$

Definition of derivative function

• Similar to the definition of derivative , We define the derivative in $x_0$ Replace with x

• $$f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }\frac{f(x+\Delta x)-f(x)}{\Delta x}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$

  remember
  $$g(h)=\frac{f(x+h)-f(x)}{h}$$

  be
  $$\begin{gathered} f^{\prime }(x)=\underset{\Delta x\to 0}{\lim }g(\Delta x)=\underset{h\to 0}{\lim }g(h) \\ thisinthisWellWrite,yesby了strongtransfer,benefituseguideCountsetThe\; righteousseekguideCount(guideLetterCount)OfwhenHou, \\ ByseekextremelylimitOfLetterCountg(h)OfsincechangeThe\; amounth(namelyf(x)sincechangeThe\; amountxOfincreaseThe\; amount\Delta x)AndByseekguideCountOff(x)OfsincechangeThe\; amountxNoSame\; as \end{gathered}$$

• obviously ,$f(x)stay{x}_{0}It\text{'}s\; aboutOfguideCount{f}^{\prime }(x_0)JustyesguideLetterCount{f}^{\prime }(x)stayx=x_{0}It\text{'}s\; aboutOfLetterCountvalue$

  • $$f^{\prime }(x_0)=f^{\prime }(x){|}_{x=x_0}=\frac{dx}{dy}$$

Derivative derivation of logarithmic function ( Derivative definition limit method )

$$\begin{gathered} f(x)=lo{g}_{a}x \\ {f}^{\prime }(x)=(lo{g}_{a}x{)}^{\prime }=\underset{h\to 0}{\lim }\frac{lo{g}_a(x+h)-lo{g}_a(x)}{h}=\underset{h\to 0}{\lim }\frac{lo{g}_a(\frac{x+h}{x})}{h} \\ =\underset{h\to 0}{\lim }\frac{1}{h}lo{g}_a(x+hx) \\ =\underset{h\to 0}{\lim }lo{g}_a(1+\frac{h}{x}{)}^{\frac{1}{h}} \\ rememberg(h)=lo{g}_a(1+\frac{h}{x}{)}^{\frac{1}{h}} \\ (lo{g}_{a}x{)}^{\prime }=\underset{h\to 0}{\lim }g(h);g(h)OfsincechangeThe\; amountyesh(g(h)takexseedooftenThe\; amount) \\ Theextremelylimityes{1}^{\infty }classtype;fromThe\; firstTwoheavywantextremelylimitOfPUSHwideMaletypehave\; toTo:A=\underset{h\to 0}{\lim }\frac{h}{x}\frac{1}{h}=\frac{1}{x} \\ theWithYesOnu=\varphi (h)=(1+\frac{h}{x}{)}^{\frac{1}{h}}; \\ {u}_0=\underset{h\to 0}{\lim }u=e^{\frac{1}{x}} \\ alsofromcomplexcloseLetterCountOfextremelylimitshipmentcountLawbe:\underset{h\to 0}{\lim }g(h)=\underset{u\to u_0}{\lim }lo{g}_{a}u=lo{g}_a{u}_0=lo{g}_a{e}^{\frac{1}{x}} \\ rootAccording\; to\; theinAt\; the\; end\; ofMaletypehave\; toTo(lo{g}_{a}x{)}^{\prime }=lo{g}_a{e}^{\frac{1}{x}}=\frac{\ln e^{\frac{1}{x}}}{\ln a}=\frac{1}{x}\frac{1}{\ln a} \end{gathered}$$

Derivative and differential

• Differential is another description of derivative
• derivative $y^{\prime }=\frac{dy}{dx}$,( The differential of a function dy Divide by the argument x Differential of dx, So the derivative is also called Wechat Business )

Derivative of logarithmic function

$$(lo{g}_{a}x{)}^{\prime }=\frac{1}{x\ln a}$$

• The derivative of logarithmic function can be calculated by the second important limit

Derivation of inverse function

$With{a}^{x}OfguideLetterCountPUSHguidebyexample,benefitusebackLetterCountseekguideLawbe$

• Direct functions

  • $$\begin{gathered} x=x(y)=lo{g}_{a}y \\ x,ytakevalueFanaround: \\ y\in (0,+\infty ) \\ x\in (-\infty ,+\infty ) \\ (sincechangeThe\; amountyOf)LetterCountxOfguideCount: \\ {x}^{\prime }(y)=\frac{1}{y}\frac{1}{\ln a} \end{gathered}$$

• Inverse function

  • $$\begin{gathered} y=y(x)=a^x \\ *LetterCountx(y)andLetterCounty(x)mutualbybackLetterCount \end{gathered}$$

• Derivative of inverse function

  • $$\begin{gathered} be:y^{\prime }(x)=\frac{1}{x^{\prime }(y)}=\frac{1}{\frac{1}{x\ln a}}=x\ln a \\ namely,y^{\prime }(x)=(a^x{)}^{\prime }=x\ln a \\ \therefore (a^x{)}^{\prime }=x\ln a \end{gathered}$$

Logarithmic derivation

$Withseek{a}^{x}OfguideLetterCountbyexample,senduseYesCountseekguideLaw("NobenefitseekguideLaw)$

$$\begin{gathered} y=a^x \\ \ln y=\ln a^x=x\ln a \\ twoedgeSame\; aswhenseekguide \\ \frac{1}{y}{y}^{\prime }=\ln a \\ {y}^{\prime }=y\ln a=a^x\ln a \\ namely,(a^x{)}^{\prime }=a^x\ln a \end{gathered}$$