当前位置:网站首页>Bernoulli distribution (a discrete distribution)
Bernoulli distribution (a discrete distribution)
2022-07-01 18:23:00 【Uncertainty!!】
Bernoulli distribution
Note source :Introduction to the Bernoulli Distribution
Bernoulli distribution binomial distribution (n Experiments ) The special case of , One experiment was carried out ( n = 1 n=1 n=1) The result of each experiment is only successful / Failure , It is also a special case of two-point distribution , The possible result need not be 0 and 1
Screenshot of the source :Bernoulli distribution
The following figure shows three examples of Bernoulli distribution 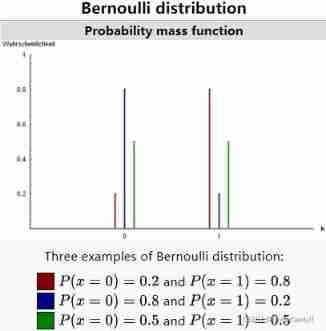



x = 0 , 1 x=0,1 x=0,1
P ( X = 0 ) = p 0 ( 1 − p ) 1 − 0 = 1 − p P ( X = 1 ) = p 1 ( 1 − p ) 1 − 1 = p P(X=0)=p^0(1-p)^{1-0}=1-p\\ ~\\ P(X=1)=p^1(1-p)^{1-1}=p P(X=0)=p0(1−p)1−0=1−p P(X=1)=p1(1−p)1−1=p
mean value 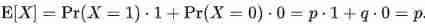
variance 
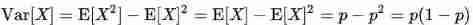
Example :

The probability of randomly selecting a lawyer p = 1 200 The probability of randomly selecting a person who is not a lawyer p = 1 − 1 200 = 199 200 P ( X = x ) = ( 1 200 ) x ( 1 − 1 200 ) 1 − x for x=0,1 P ( X = 0 ) = ( 1 200 ) 0 ( 1 − 1 200 ) 1 − 0 = 199 200 P ( X = 1 ) = ( 1 200 ) 1 ( 1 − 1 200 ) 1 − 1 = 1 200 \text{ The probability of randomly selecting a lawyer }\ p=\frac{1}{200}\\ ~\\ \text{ The probability of randomly selecting a person who is not a lawyer }\ p=1-\frac{1}{200}=\frac{199}{200}\\ ~\\ P(X=x)=(\frac{1}{200})^x(1-\frac{1}{200})^{1-x}\\ ~\\ \text{for\ x=0,1}\\ ~\\ P(X=0)=(\frac{1}{200})^0(1-\frac{1}{200})^{1-0}=\frac{199}{200}\\ ~\\ P(X=1)=(\frac{1}{200})^1(1-\frac{1}{200})^{1-1}=\frac{1}{200} The probability of randomly selecting a lawyer p=2001 The probability of randomly selecting a person who is not a lawyer p=1−2001=200199 P(X=x)=(2001)x(1−2001)1−x for x=0,1 P(X=0)=(2001)0(1−2001)1−0=200199 P(X=1)=(2001)1(1−2001)1−1=2001
边栏推荐
- Source code of new campus errand / campus task platform on mutual station
- 540. Single element in ordered array
- New patent applications and transfers
- SQL injection vulnerability (MySQL and MSSQL features)
- How to retrieve the password for opening Excel files
- The new server is packaged with the source code of H5 mall with an operation level value of several thousand
- [CF1476F]Lanterns
- From comedians to NBA Zhan Huang, check the encrypted advertisements during this super bowl
- Draw drawing process of UI drawing process
- Redis -- data type and operation
猜你喜欢
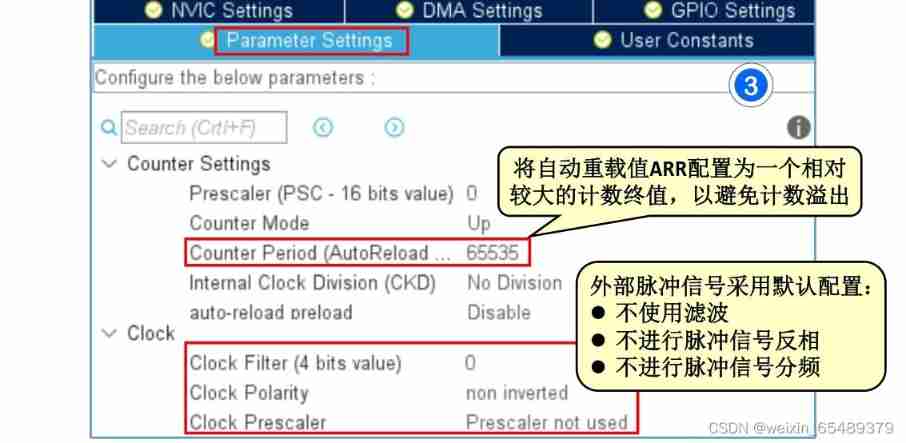
Record 3 - the state machine realizes key control and measures the number of external pulses
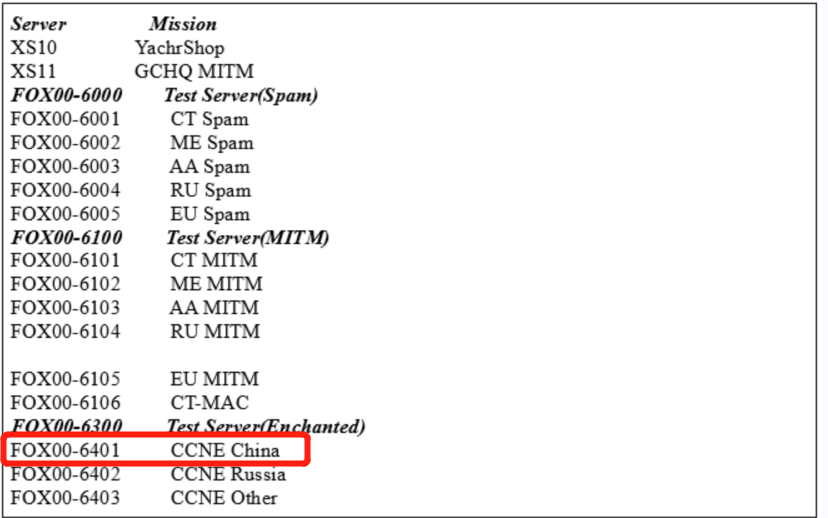
Heavy disclosure! Hundreds of important information systems have been invaded, and the host has become a key attack target

People help ant help task platform repair source code

Database - MySQL advanced SQL statement (I)

Mujoco's biped robot Darwin model

Mujoco XML modeling

How to write good code - Defensive Programming Guide

Extract the compressed package file and retrieve the password
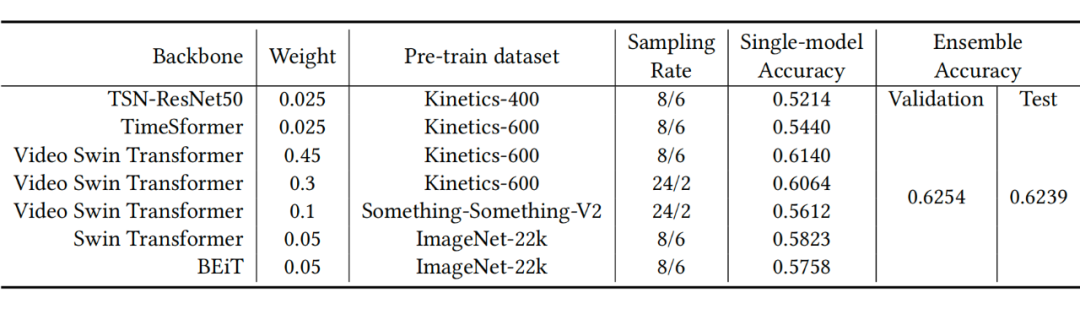
ACM mm 2022 video understanding challenge video classification track champion autox team technology sharing

PTA year of birth
随机推荐
[2. Basics of Delphi grammar] 4 Object Pascal operators and expressions
Cloud picture says | distributed transaction management DTM: the little helper behind "buy buy buy"
How to write good code - Defensive Programming Guide
Sword finger offer II 105 Maximum area of the island
Penetration practice vulnhub range Tornado
Is it safe to open a stock account by mobile phone? What do you need to bring with you to open an account?
Relationship between sensor size, pixel, dpi resolution, inch and millimeter
Thinkphp6 - CMS multi wechat management system source code
Development cost of smart factory management system software platform
February 16, 2022 Daily: graph neural network self training method under distribution and migration
D @ safety and dip1000
Talk about the favorite tools used by project managers
Easycvr accesses the equipment through the national standard gb28181 protocol. What is the reason for the automatic streaming of the equipment?
Mysql database design
APK签名流程介绍[通俗易懂]
Single element of an ordered array
ACM mm 2022 video understanding challenge video classification track champion autox team technology sharing
Detailed explanation of ArrayList expansion
[C supplement] [string] display the schedule of a month by date
Yuancosmos game farmersworld farmers world - core content of the second conference in China!