当前位置:网站首页>MATLB | real time opportunity constrained decision making and its application in power system
MATLB | real time opportunity constrained decision making and its application in power system
2022-07-06 01:16:00 【Power system code】
Catalog
2.1 Situational approach to opportunity constrained decision making
2.2 Scenario method with measurement
3、 ... and 、 A fast method of opportunity constrained decision making
3.1 Approximate adjustment through affine transformation
3.2 Affine transformation of feasible region
3.3 Two stage decision algorithm
Four 、 Numerical example —— Power distribution network
4.1 Prevent the active power reduction of overvoltage

Column directory query :* The beauty of power system and algorithm (Python&Matlab Code )
One 、 summary
Many engineering problems can be expressed as decision-making examples under uncertainty , That is, when the problem parameters are uncertain , The problem of making cost-effective decisions that satisfy certain given constraints . A natural approach is to make a decision that ensures that any possible acceptable value for an unknown parameter is feasible , So take the worst-case paradigm . In some applications , This robust approach produces programs that are easy to handle , You can find the best solution . Such a solution may be very conservative in terms of achievable performance : The decision may be affected by the extreme value of the parameter , These extreme values are extremely unlikely, but they have a serious impact on the feasible region for seeking the optimal decision .
The second method is to formulate the so-called opportunity constrained decision-making problem . In these questions , It can be tolerated that a set of parameter values with the minimum probability measure in the parameter space can violate the constraints of the problem , Therefore, it is unlikely to achieve . This approach allows for security ( Aimed at the probability of violating the constraint ) And performance ( Cost of decision ) Weigh against . Chance constrained problems are usually nonconvex and difficult to solve , Even if the original problem with known parameter values is convex . However , They can be effectively solved by adopting the so-called scenario method , Random constraints are replaced by deterministic constraints , By sampling the parameter uncertainty . If the number of constraints is large enough , Then the feasibility in the sense of opportunity constraint can be guaranteed with high confidence . contrary , It can also guarantee the cost of the solution obtained by this method .
In this paper , We consider the chance constrained decision-making problem with a specific structure : One side , We assume that some prior information about the unknown parameters of the decision problem is known , Exist in the form of samples ; On the other hand , We assume that further information about the true values of these parameters can be collected through measurements . We specialize in the scenario approach , So that prior samples and available metrics can be used effectively , To generate feasible regions that meet opportunity constraints . This leads to a two-stage algorithm , It consists of offline pretreatment of samples , Then there is the online part , It needs to be carried out immediately when the measurement is available . The online part is very lightweight in terms of computing time and memory consumption , Therefore, it is suitable for implementation in embedded systems . As an application of choice , We consider the control of micro generators in Distribution Networks .
In the second section , We briefly reviewed the scenario approach , The decision-making problem with limited opportunities is formulated by measurement . In the third section , Shows how to approximate the posterior distribution of unknown parameters , And a fast algorithm for solving chance constrained decision-making problem is analyzed . In section four , It shows the effectiveness of the proposed real-time operation algorithm of distribution network .
Two 、 mathematical model
2.1 Situational approach to opportunity constrained decision making
Consider opportunity constrained decision making :
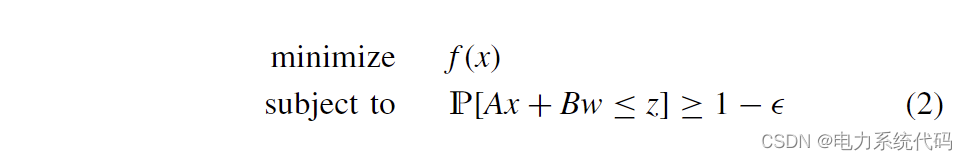
among x ∈ Rn It's a decision variable ,f (x) It's convex cost , Are unknown disturbances modeled as random variables ,
Are unknown disturbances modeled as random variables , It's a constant term . Let's assume that random variables w The support of is given a σ - Algebra. D also P stay D Defined on the . Last , ∈ (0, 1) Is the expected probability of violating the constraint .
It's a constant term . Let's assume that random variables w The support of is given a σ - Algebra. D also P stay D Defined on the . Last , ∈ (0, 1) Is the expected probability of violating the constraint .
The general chance constrained decision problem is nonconvex , And it is usually difficult to deal with in calculation . Please note that , We assume that linear constraints are affine in random variables . under these circumstances , as long as w The basic distribution of is known , You can get the analysis results , Provide conditions for the opportunity constrained problem to be reformulated as a convex problem . In any other case , Scenario methods are all about transforming random programs into deterministic problems in this form :
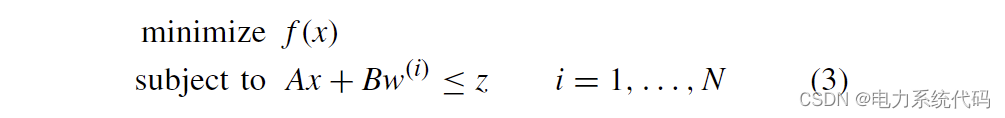
among  It is a random disturbance N Samples . If N Large enough , Then this mathematical description is equivalent to the above one .
It is a random disturbance N Samples . If N Large enough , Then this mathematical description is equivalent to the above one .
The scene method is obviously not distributed , This means that there is no interference w Make any assumptions about the probability distribution . By the amount that needs to be sampled according to such a distribution  , About w The distributed information still exists implicitly . This feature of the scene method makes it impossible to obtain a reliable interference first principle model , But applications that can use historical data are very attractive .
, About w The distributed information still exists implicitly . This feature of the scene method makes it impossible to obtain a reliable interference first principle model , But applications that can use historical data are very attractive .
2.2 Scenario method with measurement
In some applications , About interference w Online information may be available . for example , Although it may be possible to obtain information about w Prior information of distribution , But some direct measurements may be made when making a decision . We formalize the opportunity constrained decision-making problem with measurement as :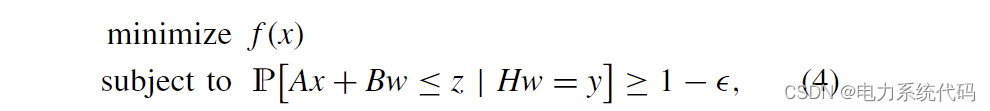
among y = Hw It is a linear measurement of disturbance , among H It is the rank of the whole bank ,![\mathbb{P}[\cdot \mid \cdot]](http://img.inotgo.com/imagesLocal/202207/06/202207060112178722_3.gif) The conditional probability . Direct application of scenario method , Such as (3) Medium , The deterministic optimization equation in the following form will be generated :
The conditional probability . Direct application of scenario method , Such as (3) Medium , The deterministic optimization equation in the following form will be generated :
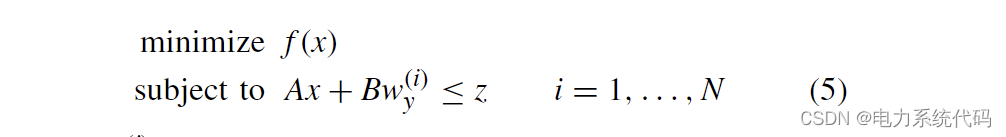
among  Is measured by y = Hw Samples of the determined conditional probability distribution .
Is measured by y = Hw Samples of the determined conditional probability distribution .
The last setting seems to offset the effectiveness of the real-time operation scenario method , Because samples 
Only in measurement y You need to generate . The use of historical samples makes the integration of this new information difficult . Besides , The resulting optimization problem (5) There are still a lot of typical redundancy constraints , This poses a computational challenge to the direct use of scenario methods for fast real-time decision-making . In the next section , We will show how to successfully solve these two problems through the offline preprocessing phase of the sample , Then there is the decision-making step driven by online measurement .
3、 ... and 、 A fast method of opportunity constrained decision making
3.1 Approximate adjustment through affine transformation
3.2 Affine transformation of feasible region
3.3 Two stage decision algorithm
Four 、 Numerical example —— Power distribution network
4.1 Prevent the active power reduction of overvoltage
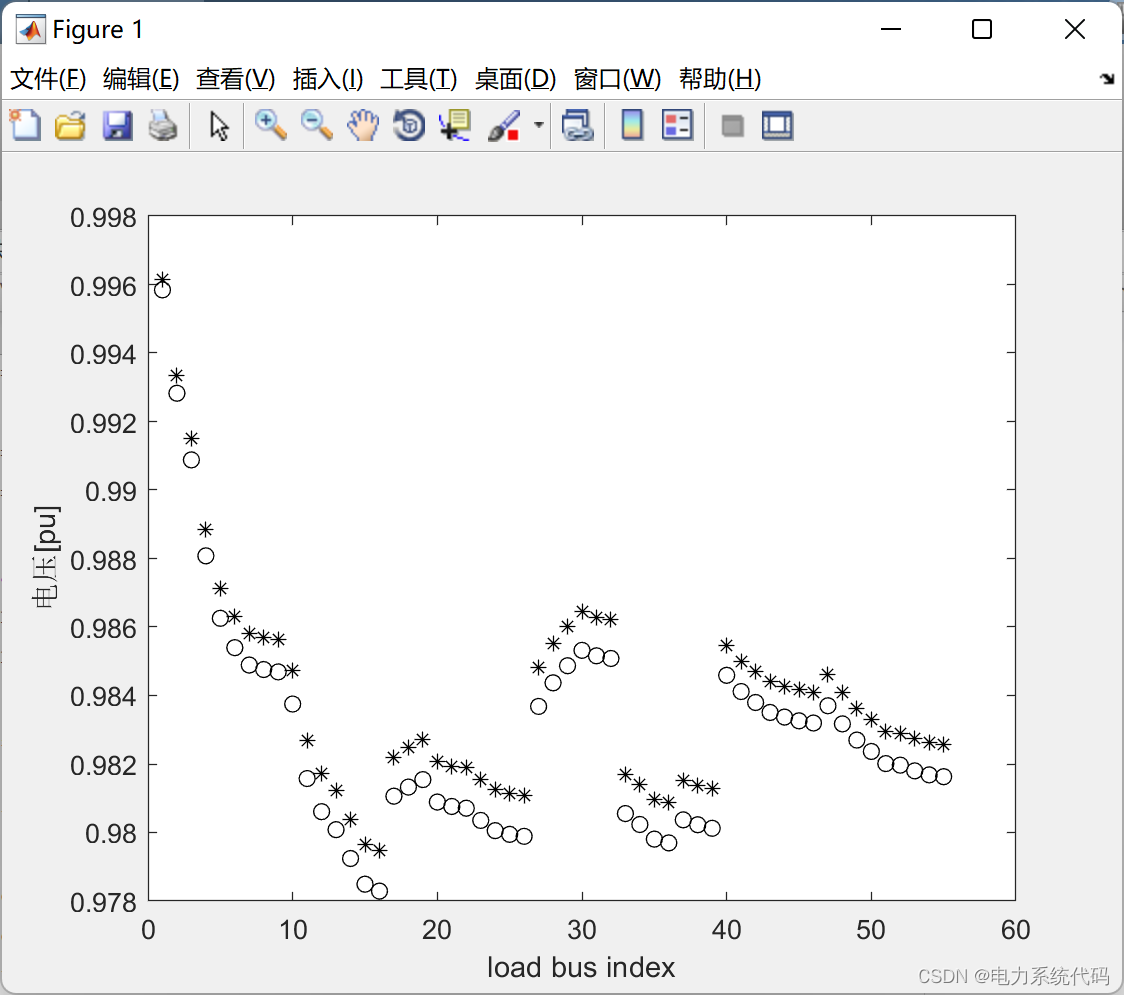
4.2 Numerical simulation
4.3 Matlab Realization
Only part of the code is shown here , See : We are shipping your work details
%% ==== Robust optimization ===========
disp(' Robust ')
gmax = (vmax - 1) / max(Rg);
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
title(sprintf(' Robust optimization —— Power generation :% 0.3f MW', gmax));
ylabel(' voltage [p.u.]');
%% expect
disp(' expect ')
Ed = mean(historicalPowerDemands, 2);
gmax = min((vmax - 1 + R*Ed)./Rg);
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
title(sprintf(' Expected optimization - Power generation :%0.3f MW', gmax));
ylabel(' voltage [p.u.]');
%% Opportunity constraints
disp(' gaussian ')
dstd = std(R(genBus,:)*historicalPowerDemands);
gmax = min((vmax - 1 + R(genBus,:)*Ed - 1.6449*dstd)./Rg(genBus));
voltageSeries = testCurtailmentStrategy(testGrid, historicalPowerDemands, gmax);
percentilePlot(voltageSeries);
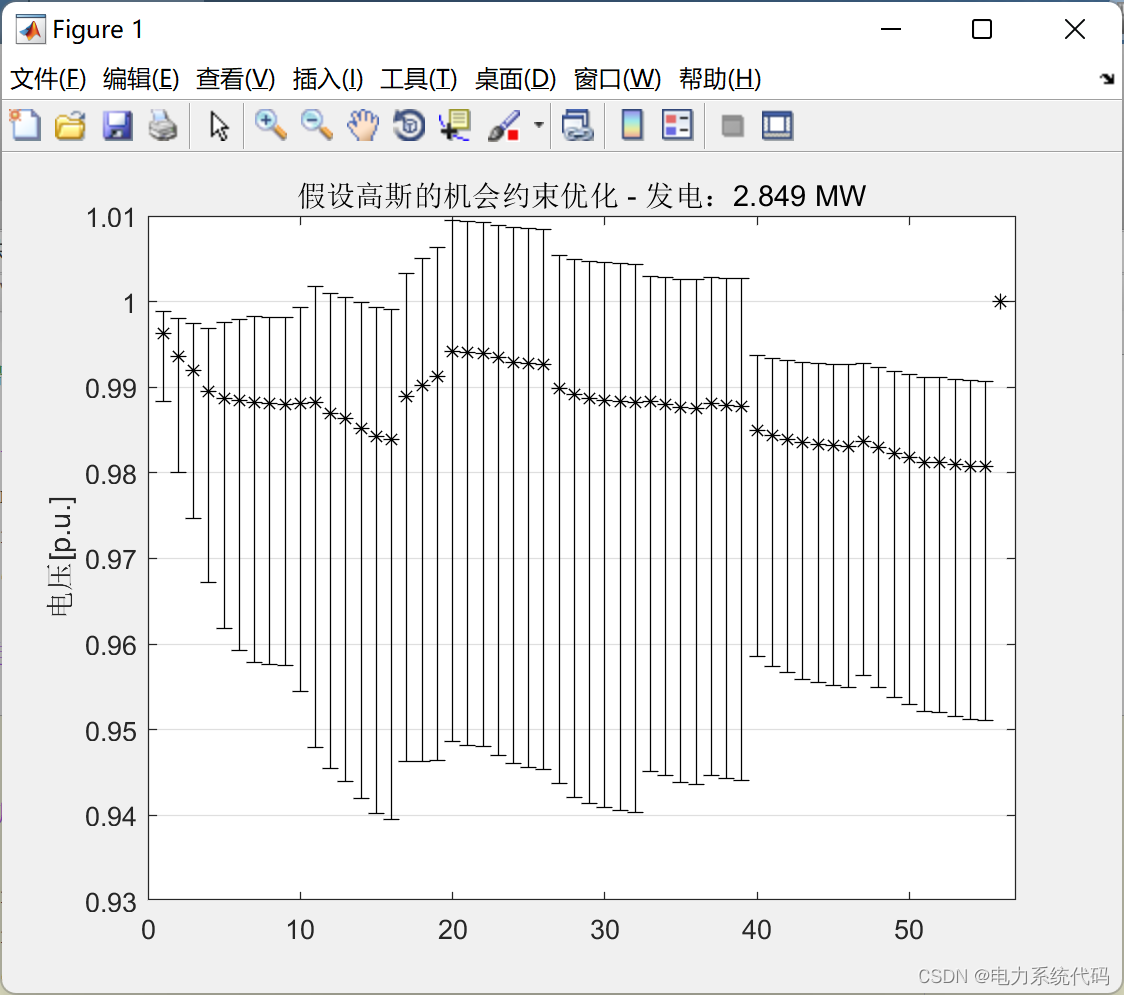
title(sprintf(' Suppose Gauss's chance constrained optimization - Electricity generation :%0.3f MW', gmax));
ylabel(' voltage [p.u.]');4.4 Running results

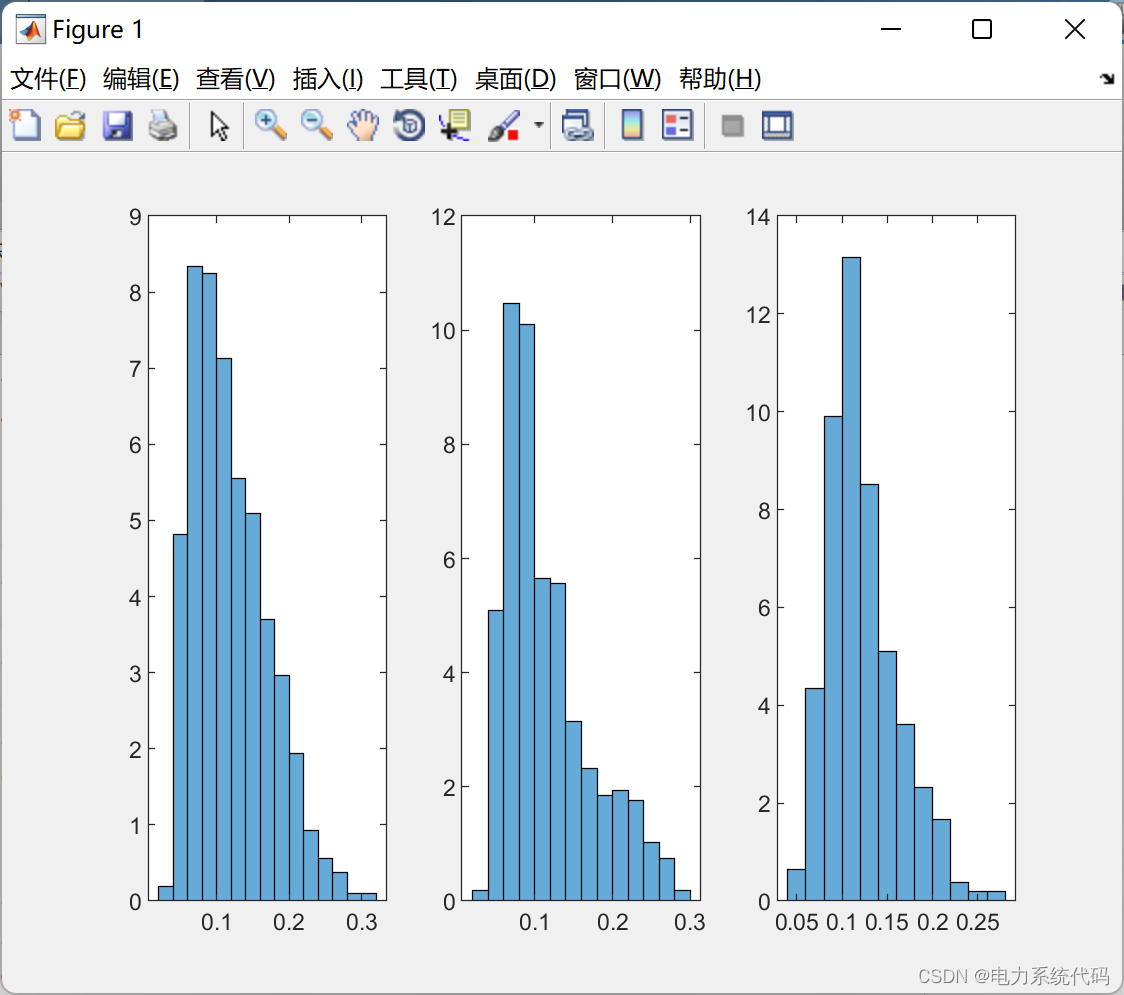
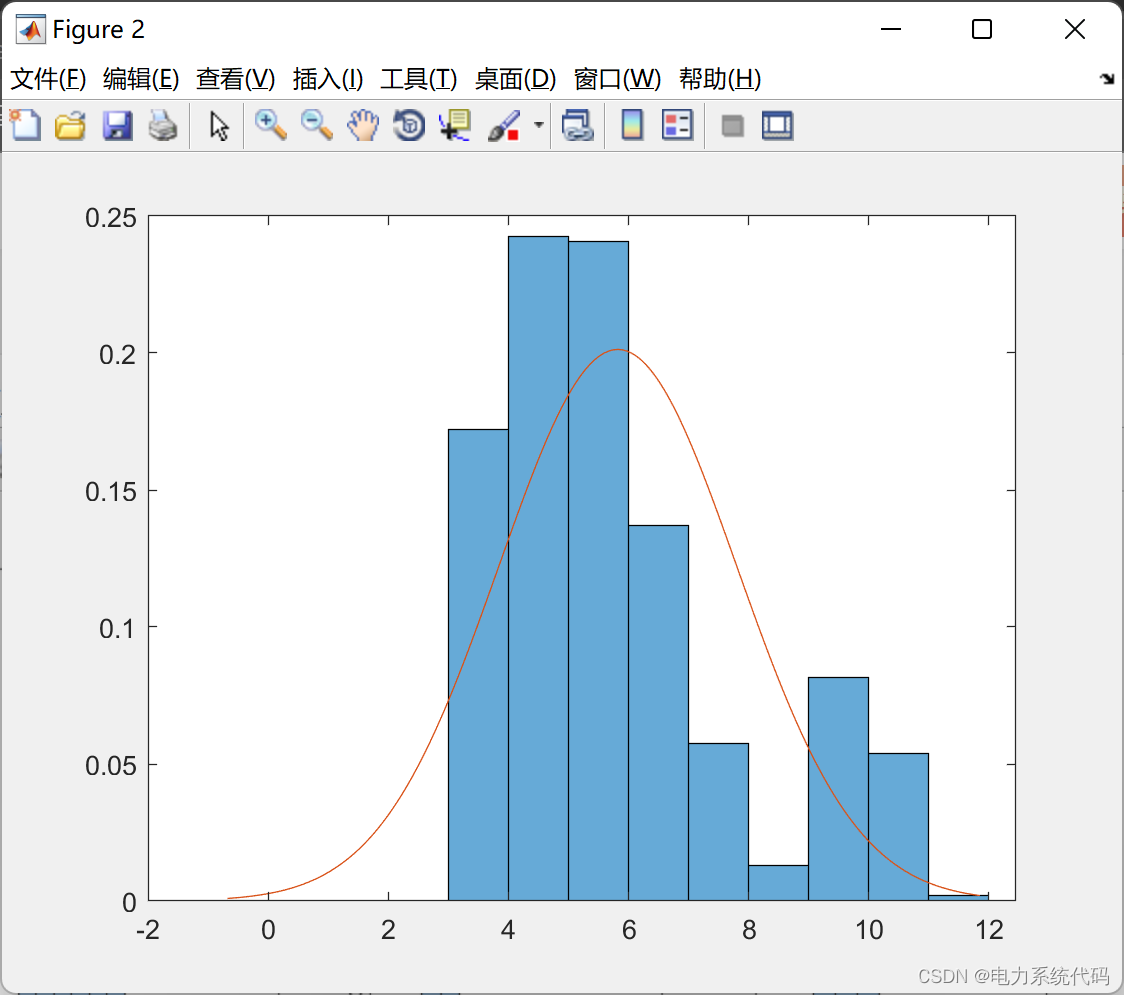
边栏推荐
- Blue Bridge Cup embedded stm32g431 - the real topic and code of the eighth provincial competition
- ubantu 查看cudnn和cuda的版本
- After 95, the CV engineer posted the payroll and made up this. It's really fragrant
- MATLB|实时机会约束决策及其在电力系统中的应用
- Differences between standard library functions and operators
- A preliminary study of geojson
- Leetcode 208. 实现 Trie (前缀树)
- MIT doctoral thesis | robust and reliable intelligent system using neural symbol learning
- 直播系统代码,自定义软键盘样式:字母、数字、标点三种切换
- Recoverable fuse characteristic test
猜你喜欢

ORA-00030

MIT doctoral thesis | robust and reliable intelligent system using neural symbol learning

Cf:c. the third problem

cf:D. Insert a Progression【关于数组中的插入 + 绝对值的性质 + 贪心一头一尾最值】

Some features of ECMAScript
vSphere实现虚拟机迁移
Who knows how to modify the data type accuracy of the columns in the database table of Damon
Fibonacci number
Xunrui CMS plug-in automatically collects fake original free plug-ins

About error 2003 (HY000): can't connect to MySQL server on 'localhost' (10061)
随机推荐
基于DVWA的文件上传漏洞测试
VMware Tools安装报错:无法自动安装VSock驱动程序
程序员搞开源,读什么书最合适?
Cglib dynamic agent -- example / principle
The basic usage of JMeter BeanShell. The following syntax can only be used in BeanShell
Threedposetracker project resolution
Idea sets the default line break for global newly created files
Netease smart enterprises enter the market against the trend, and there is a new possibility for game industrialization
Study diary: February 13, 2022
Cannot resolve symbol error
Vulhub vulnerability recurrence 75_ XStream
Blue Bridge Cup embedded stm32g431 - the real topic and code of the eighth provincial competition
2020.2.13
普通人下场全球贸易,新一轮结构性机会浮出水面
毕设-基于SSM高校学生社团管理系统
95后CV工程师晒出工资单,狠补了这个,真香...
What is the most suitable book for programmers to engage in open source?
ORA-00030
Some features of ECMAScript
How to get the PHP version- How to get the PHP Version?