当前位置:网站首页>[day 30] given an integer n, find the sum of its factors
[day 30] given an integer n, find the sum of its factors
2022-07-06 00:52:00 【Stubble】
Learning Guide
order 、 Column Preface
This column opens , The purpose is to help everyone better master learning Java, Especially some Java Learners' It is difficult to find systematic algorithm learning materials on the Internet to help you get started with algorithms , At the same time, if you have any questions about the contents of the column, you can add my wechat at the end of the article to give you a one-to-one explanation .
But the most important thing is to think independently , For all the content of this column , Be able to fully master , Write the code completely by yourself , There must be no problem getting started with the algorithm .
The learning of algorithm must not be short of summary , Here I recommend that you can go to University algorithm community Punch in the learned knowledge , To consolidate and review .
The only way to learn algorithms well must be Topic sea strategy , Only by accumulating a lot of practice can you practice your skills . Any topic of the column I will start with 【 Title Description 】【 Their thinking 】【 Template code 】【 Code parsing 】 Wait for four plates to explain .
One 、【 Example 1】
1、 Title Description
Given an integer n ( 1 ≤ n ≤ 1 e 9 ) n(1\leq n\leq1e9) n(1≤n≤1e9), Find the sum of its divisors , The answer is right 1 e 9 + 7 1e9+7 1e9+7 modulus
2、 Their thinking
( 1 ) (1) (1) You can find the number of factors according to the code , Yes O ( n ) O(n) O(n) and O ( n ) O(\sqrt n) O(n) Complex approach .
( 2 ) (2) (2) It can also be solved by the sum of approximations theorem , Focus on the theorem
3、 Template code
1) simple O(n) practice
import java.util.*;
public class Main {
static int mod=1000000007;
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
long ans=0;
for (int i = 1; i <=n; i++) {
if (n%i==0) ans=(ans+i)%mod;
}
System.out.println(ans);
}
}
2) Optimize root n practice
import java.util.*;
public class test {
static int mod=1000000007;
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
long ans=0;
for (int i = 1; i <=n/i; i++) {
if (n%i==0){
if (i!=n/i){
ans=(ans+i)%mod;
ans=(ans+n/i)%mod;
}else{
ans=(ans+i)%mod;
}
}
}
System.out.println(ans);
}
}
3) Sum of divisors theorem
import java.util.*;
public class test {
static int mod=1000000007;
public static void main(String[] args){
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
long sum=1;
for (int i = 2; i <=n/i; i++) {
if (n%i==0){
int c=0;
while (n%i==0){
c++;
n/=i;
}
long t=1;
while (c-->0) t=(t*i+1)%mod;
sum=(sum*t)%mod;
}
}
if (n>1) sum=(sum*(n+1)%mod);
System.out.println(sum);
}
}
4、 Code parsing
- ( 1 ) (1) (1) I talked about it before. , For a positive integer n n n, From the basic theorem of the formula :
n = ∏ i = 1 k p i i = p 1 a 1 × p 2 a 2 × p 3 a 3 . . . . . . p k a k ( p 1 , p 2 . . . . p k all by quality Count ) n=\prod_{i=1}^{k} p_i^{^i}=p_1^{a^1}\times p_2^{a^2}\times p_3^{a^3}......p_k^{a^k}(p_1,p_2....p_k All are prime numbers ) n=i=1∏kpii=p1a1×p2a2×p3a3......pkak(p1,p2....pk all by quality Count )
So remember n n n The sum of constraints is f ( n ) f(n) f(n), Then there are :
f ( n ) = ( p 1 0 + p 1 1 + . . . + p 1 a 1 ) ∗ ( p 2 0 + p 2 1 + . . . + p 2 a 2 ) ∗ . . . ( p k 0 + p k 1 + . . . + p k a k ) f(n)=(p_1^0+p_1^1+...+p_1^{a_1})*(p_2^0+p_2^1+...+p_2^{a_2})*...(p_k^0+p_k^1+...+p_k^{a_k}) f(n)=(p10+p11+...+p1a1)∗(p20+p21+...+p2a2)∗...(pk0+pk1+...+pkak) - ( 2 ) (2) (2) prove :
First calculate p 1 a 1 p_1^{a_1} p1a1 Sum of divisors of , It can be seen that ( p 1 0 + p 1 1 + . . . + p 1 a 1 ) (p_1^0+p_1^1+...+p_1^{a_1}) (p10+p11+...+p1a1)
Second, calculate p 2 a 2 p_2^{a_2} p2a2 Sum of divisors of , It can be seen that ( p 2 0 + p 2 1 + . . . + p 2 a 2 ) (p_2^0+p_2^1+...+p_2^{a_2}) (p20+p21+...+p2a2)
…
Finally, I worked out p k a k p_k^{a^k} pkak Sum of divisors of , It can be seen that ( p k 0 + p k 1 + . . . + p k a k ) (p_k^0+p_k^1+...+p_k^{a_k}) (pk0+pk1+...+pkak)
According to the principle of multiplication , n n n Sum of divisors of f ( n ) by : f(n) by : f(n) by :
f ( n ) = ( p 1 0 + p 1 1 + . . . + p 1 a 1 ) ∗ ( p 2 0 + p 2 1 + . . . + p 2 a 2 ) ∗ . . . ( p k 0 + p k 1 + . . . + p k a k ) f(n)=(p_1^0+p_1^1+...+p_1^{a_1})*(p_2^0+p_2^1+...+p_2^{a_2})*...(p_k^0+p_k^1+...+p_k^{a_k}) f(n)=(p10+p11+...+p1a1)∗(p20+p21+...+p2a2)∗...(pk0+pk1+...+pkak)
Two 、【 Example 2】
1、 Title Description
Given n n n A positive integer a i a_i ai, Please output the sum of divisors of the product of these numbers , The answer is right 1 0 9 + 7 10^9+7 109+7 modulus .
2、 Their thinking
( 1 ) (1) (1) On the last question , From the sum of the factors of a number to multiple numbers , But in essence, the final product is still a number .
( 2 ) (2) (2) We can n n n All numbers are decomposed by prime factors , Count the total number of occurrences of each prime factor , Finally, use the sum of divisors theorem .
3、 Template code
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class Main {
static final int mod = 1000000007;
static Map<Integer, Integer> map = new HashMap<>();
static long ans = 1;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
while (n-- > 0) {
int a = sc.nextInt();
getNums(a);
}
for (Integer a : map.keySet()) {
long sum=1;
int k=map.get(a);
while(k-->0) sum=(sum*a+1)%mod;
ans=(ans*sum)%mod;
}
System.out.print(ans);
}
// Formula for finding prime factor
static void getNums(int n) {
for (int i = 2; i <= n / i; i++) {
while (n % i == 0) {
map.put(i, map.getOrDefault(i, 0) + 1);
n /= i;
}
}
if (n > 1) map.put(n, map.getOrDefault(n, 0) + 1);
}
}
3、 ... and 、 Recommendation column
Four 、 After-school exercises
| Serial number | Topic link | Difficulty rating |
|---|---|---|
| 1 | Sum of divisors | 2 |
边栏推荐
- 【文件IO的简单实现】
- Analysis of the combination of small program technology advantages and industrial Internet
- Installation and use of esxi
- Curlpost PHP
- Reading notes of the beauty of programming
- Fibonacci number
- Browser reflow and redraw
- 激动人心,2022开放原子全球开源峰会报名火热开启
- 如何制作自己的机器人
- Set data real-time update during MDK debug
猜你喜欢
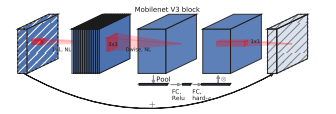
MobileNet系列(5):使用pytorch搭建MobileNetV3并基于迁移学习训练
Free chat robot API
95后CV工程师晒出工资单,狠补了这个,真香...
View class diagram in idea
Building core knowledge points

KDD 2022 | EEG AI helps diagnose epilepsy
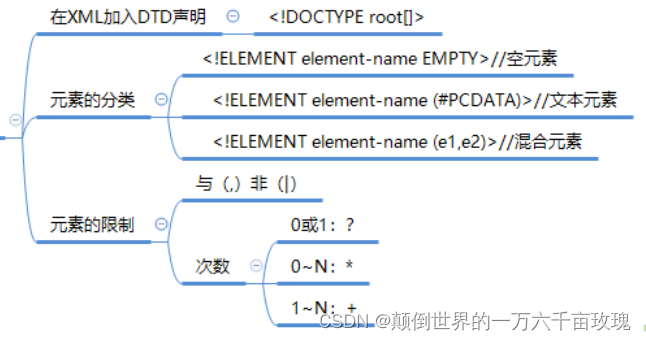
XML Configuration File

Ubantu check cudnn and CUDA versions

Intensive learning weekly, issue 52: depth cuprl, distspectrl & double deep q-network
Spark SQL空值Null,NaN判断和处理
随机推荐
C language programming (Chapter 6 functions)
Zhuhai's waste gas treatment scheme was exposed
Yolov5, pychar, Anaconda environment installation
KDD 2022 | 脑电AI助力癫痫疾病诊断
After Luke zettlemoyer, head of meta AI Seattle research | trillion parameters, will the large model continue to grow?
Problems and solutions of converting date into specified string in date class
Study diary: February 13, 2022
The value of applet containers
Extension and application of timestamp
Getting started with devkit
golang mqtt/stomp/nats/amqp
毕设-基于SSM高校学生社团管理系统
[groovy] JSON serialization (jsonbuilder builder | generates JSON string with root node name | generates JSON string without root node name)
Cannot resolve symbol error
Fibonacci number
猿桌派第三季开播在即,打开出海浪潮下的开发者新视野
Spark SQL UDF function
[simple implementation of file IO]
MCU realizes OTA online upgrade process through UART
直播系统代码,自定义软键盘样式:字母、数字、标点三种切换