Mlsys 2020 | fedprox: Federation optimization of heterogeneous networks

Preface

subject ： Federated Optimization for Heterogeneous Networks
meeting ： Conference on Machine Learning and Systems 2020
Address of thesis ：Federated Optimization for Heterogeneous Networks

FedAvg There is no good solution to device heterogeneity and data heterogeneity ,FedProx stay FedAvg Some improvements have been made to try to alleviate these two problems .

stay Online Learning in , In order to prevent the model from departing too far from the original model after being updated according to the new data , That is to prevent over regulation , Usually, a remainder term is added to limit the difference of model parameters before and after updating .FedProx A remainder is also introduced in , Works in a similar way .

I. FedAvg

Google Our team proposed federal learning for the first time , And the basic algorithm of Federated learning is introduced FedAvg. The general form of the problem ：

The formula 1：$f_i(w)=l(x_i,y_i;w)$ It means the first one $i$ Loss of samples , That is to minimize the average loss of all samples .

The formula 2：$F_k(w)$ Represents the average loss of all data in a client ,$f(w)$ Represents the weighted average loss of all clients under the current parameter .

It is worth noting that , If all $P_k$（ The first k Client data ） It is formed by randomly and evenly distributing the training samples on the client , So each of these $F_k(w)$ Our expectations are $f(w)$. This is usually done by distributed optimization algorithms IID hypothesis ： That is, the data of each client is independent and identically distributed .

FedAvg：

Simply speaking , stay FedAvg Under the framework of ： In every round of communication , The server distributes global parameters to each client , Each client uses local data to train the same epoch, Then upload the gradient to the server for aggregation to form the updated parameters .

FedAvg There are two defects ：

1. Device heterogeneity ： The communication and computing capabilities of different devices are different . stay FedAvg in , The selected clients train the same locally epoch, Although the author points out that promotion epoch It can effectively reduce the communication cost , But the bigger epoch Next , There may be a lot of equipment that can't complete the training on time . Whether it's direct drop Drop this part of the client model or directly use this part of the unfinished model to aggregate , Will have a bad impact on the convergence of the final model .
2. Data heterogeneity ： Data in different devices may be non independent and identically distributed . If the data is independent and identically distributed , Then the local model training epoch Larger will only accelerate the convergence of the global model ; If not identically distributed , When different equipment uses local data for training and the number of training rounds is large , The local model will deviate from the original global model .

II. FedProx

In order to alleviate the above two problems , The author of this paper proposes a new federal learning framework FedProx.FedProx Can handle heterogeneity well .

To define a ：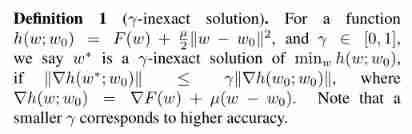

So-called $\gamma$ inexact solution： For an objective function to be optimized $h(w;w_0)$, If there is ：
$$||\nabla h(w^{\ast };w_0)||\le \gamma ||\nabla h(w_0;w_0)||$$
here $\gamma \in [0,1]$, We said $w^{\ast }$ yes $h$ One of the $\gamma -$ Inexact solution .

For this definition , We can understand it as ： The smaller the gradient, the more accurate , Because the greater the gradient , It takes more time to converge . So obviously ,$\gamma$ The smaller it is , Explain $w^{\ast }$ The more accurate .

We know , stay FedAvg in , equipment $k$ When training locally , The objective function that needs to be minimized is ：
$$F_k(w)=\frac{1}{n_k}\sum _{i\in P_k}{f}_i(w)$$
Simply speaking , Every client is an optimization loss function , This is a normal idea , Make the global model perform better on local datasets .

But if the data between devices is heterogeneous , The model obtained after optimization of each client is too different from the global model allocated by the server at the beginning , The local model will deviate from the original global model , This will slow down the convergence of the global model .

In order to effectively limit this deviation , The author of this paper proposes , equipment $k$ When training locally , The following objective functions need to be minimized ：
$$h_k(w;w^t)=F_k(w)+\frac{\mu }{2}||w-w^t|{|}^2$$
The author in FedAvg Based on the loss function , Introduced a proximal term, We can call it the proximal term . After introducing the proximal term , The model parameters obtained by the client after local training $w$ It will not be associated with the initial server parameters $w^t$ Too much deviation .

By observing the above formula, we can find , When $\mu =0$ when ,FedProx The optimization goal of the client is similar to FedAvg Agreement .

This idea is actually very common , In machine learning , To prevent over regulation , Or to limit parameter changes , Usually, such a similar term will be added to the original loss function . For example, in online learning , We can add this item , To prevent the original model from deviating too much from the original model after online updating with new data .

FedProx Algorithm pseudo code of ：

Input ： Total number of clients $K$、 Number of communication rounds $T$、$\mu$ and $\gamma$、 Server initialization parameters $w^0$, Number of selected clients $N$, The first $k$ Probability of clients being selected $p_k$.

For every round of communication ：

1. The server starts with probability $p_k$ Select a batch of clients randomly , Their collection is $S_t$.
2. The server will set the current parameters $w^t$ Send to the selected client .
3. Each selected client needs to find one $w_k^{t+1}$, there $w_k^{t+1}$ No more FedAvg According to local data SGD Optimized , It's about optimization $h_k(w;w^t)$ Later obtained $\gamma -$ Inexact solution .
4. Each client passes the inexact solution back to the server , The server aggregates these parameters to get the next round of initial parameters .

By observing this step, we can find ,FedProx stay FedAvg Two improvements have been made on ：

1. The near term is introduced , Limits model deviation due to data heterogeneity .
2. An inexact solution is introduced , Each client no longer needs to train the same number of rounds , Just get an inexact solution , This effectively relieves the calculation pressure of some equipment .

III. experiment

chart 1 The influence of data heterogeneity on the convergence of the model is given ：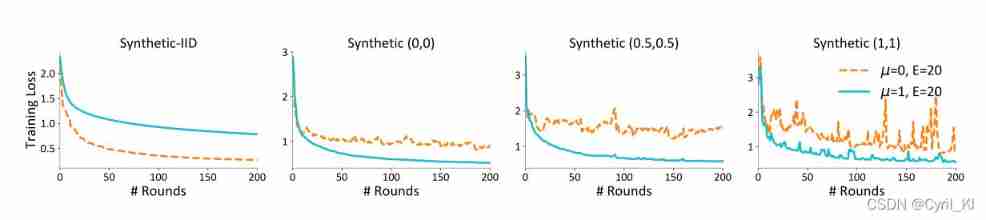

The figure above shows how the loss changes as the number of communication rounds increases , The heterogeneity of data increases from left to right , among $\mu =0$ Express FedAvg. You can find , The stronger the heterogeneity between data , Worse convergence , But if we let $\mu >0$, Will effectively alleviate this situation , That is, the model will converge faster .

chart 2：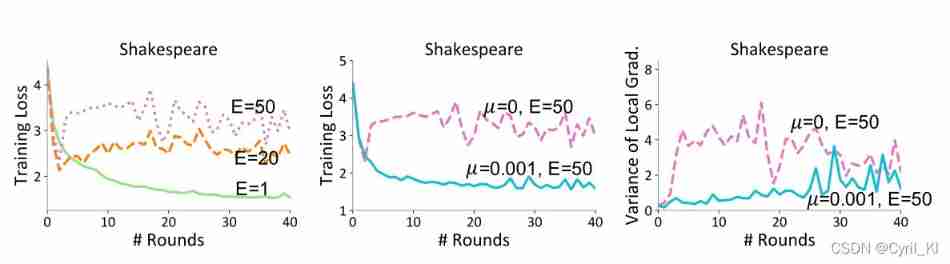

On the left ：E After adding, it is necessary to $\mu =0$ The impact of the situation . You can find , Too much local training will cause the model to deviate from the global model , Convergence slows .

Chinese ： The same data set , increase $\mu$ after , Convergence will accelerate , Because this effectively alleviates the model offset , So that FedProx The performance of depends less on $E$.

The author gives a trick： In practice ,$\mu$ It can be selected adaptively according to the current performance of the model . The simpler way is to increase when the loss increases $\mu$, When the loss decreases $\mu$.

But for $\gamma$, The author doesn't seem to specify how to choose , Can only go to GitHub Study the source code and then give an explanation .

IV. summary

The heterogeneity of data and devices is important to traditional FedAvg The algorithm presents a challenge , The author of this paper FedAvg On the basis of that, the paper puts forward FedProx,FedProx Compared with FedAvg There are two main differences ：

1. The differences in communication and computing capabilities of different devices are considered , And the inexact solution is introduced , Different equipment does not need to train the same number of rounds , Just get an inexact solution .
2. The near term is introduced , In the case of heterogeneous data , It limits the deviation of the local training model from the global model .