当前位置:网站首页>Simple implementation of AVL tree insertion and verification operations
Simple implementation of AVL tree insertion and verification operations
2022-07-07 03:56:00 【Wuhu kaichong ~】
Catalog
Insert the new node as a binary search tree
Adjust the balance factor of the node (*****)
AVL The concept of tree
Although binary search tree can shorten the search efficiency , However, if the data is ordered or close to ordered, the binary search tree will degenerate into a single branch tree , Finding elements is equivalent to searching for elements in the sequence table , inefficiency . therefore , Two Russian mathematicians G.M.Adelson-Velskii and E.M.Landis stay 1962 In, he invented a method to solve the above problems : When a new node is inserted into the binary search tree , If we can ensure that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1( You need to adjust the nodes in the tree ), You can reduce the height of the tree , This reduces the average search length .
That is to say , These two people have done some optimization on the basis of binary tree search tree , The original binary search tree may degenerate into a single tree , The search time complexity is O(n), Now we ensure that the tree is basically balanced , So the time complexity of search becomes O(logn)
AVL Characteristics of trees
A tree AVL Trees , Or it's an empty tree , Or have these two characteristics
Its left and right subtrees are AVL Trees
The difference between the height of the left and right subtrees ( It's called equilibrium factor ) The absolute value of is not more than 1(-1/0/1)If a binary search tree is highly balanced , It is AVL Trees . If it has n Nodes , Its height can be maintained at , Search time complexity O( logn).
As for the balance factor , Simple , Just add a variable belonging to the balance factor when defining tree nodes
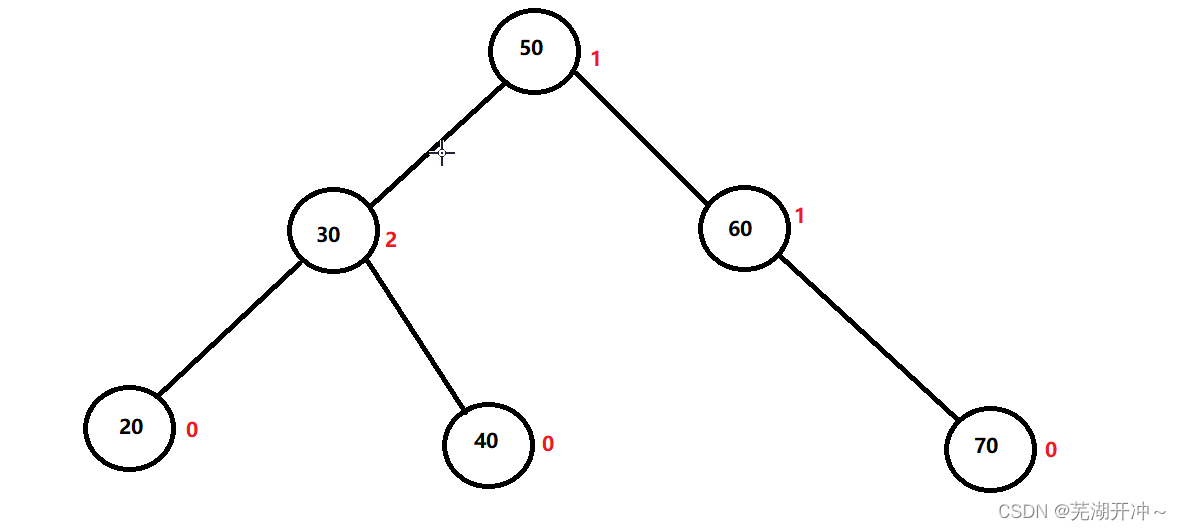
Here is another picture , Let's feel
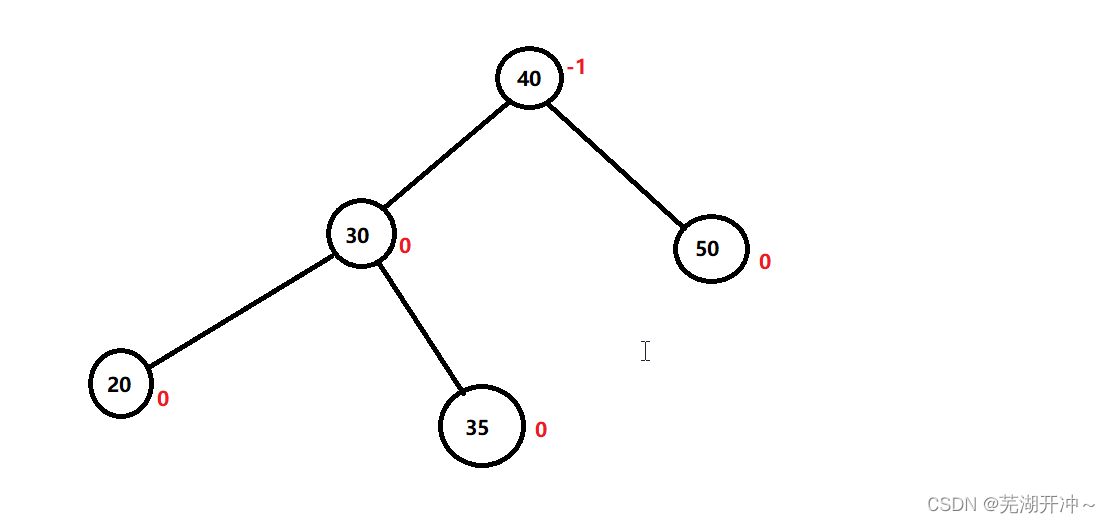
The number in the circle represents the value of the node , The red number indicates the balance factor of the node , The balance factor can be subtracted from the left subtree by the right subtree , You can also subtract the right subtree from the left subtree , Here we use the right subtree minus the left subtree , The same goes for the bottom
AVL Definition of tree node
template <class T>
class AVLTreeNode {
public:
AVLTreeNode<T>* _left;
AVLTreeNode<T>* _right;
AVLTreeNode<T>* _parent;
T _value;
int _bf; // Balance factor , The agreed balance factor is the height of the right tree minus the height of the left tree
// Constructors
AVLTreeNode(const T& value = T())
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_value(value)
,_bf(0)
{}
};In this node, we use the parent expression , Because parents are needed later , It's a little complicated
preparation
template <class T>
class AVLTree {
typedef AVLTreeNode<T> Node;
public:
AVLTree()
:_root(nullptr)
{}
~AVLTree() {
Distory(_root);
}
private:
void Distory(Node*& root) {
if (root) {
Distory(root->_left);
Distory(root->_right);
delete root;
root = nullptr;
}
}
Node* _root;
};Be careful Distory The parameter is Node* References to
AVL Insertion of trees
Insert the new node as a binary search tree
We first insert it according to the insertion method of binary search tree , It doesn't matter if you can't insert a binary search tree , Just look directly here
bool Insert(const T& value) {
// Determine the position to insert
// If AVL The tree is empty.
if (_root == nullptr) {
_root = new Node(value);
return true;
}
// If AVL The tree is not empty
// Find node , Insert it first ;
Node* parent = _root;
Node* child = parent;
while (child) {
parent = child;
if (value > child->_value) {
child = child->_right;
}
else if (value < child->_value) {
child = child->_left;
}
else {
return false;
}
}
// Node found , Insert , Update the pointer in the node
child = new Node(value);
child->_parent = parent;
if (child->_value > parent->_value) {
parent->_right = child;
}
else {
parent->_left = child;
}
Be careful , The above function is not finished , Just because it's too long , So it is divided into two parts
Adjust the balance factor of the node (*****)
Five stars , A top priority
First, let's talk about four ways to adjust the balance factor , Left spin , Right single spin , Right left double rotation , Double left and right
But in fact, we only see one , The others are simple
Let's look at left monocyclone
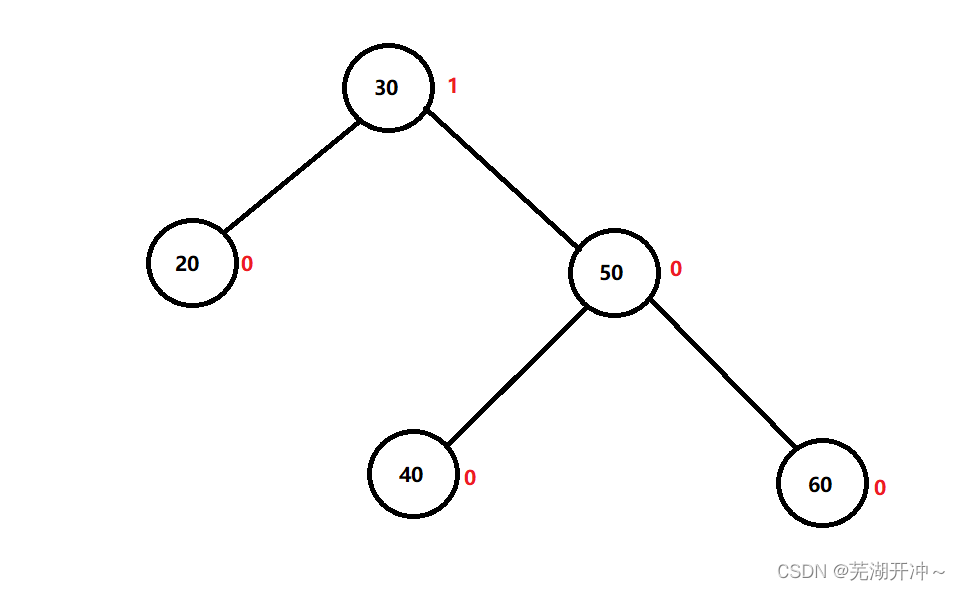
Look at this picture , Now it is balanced , But if we add another 70, It is unbalanced
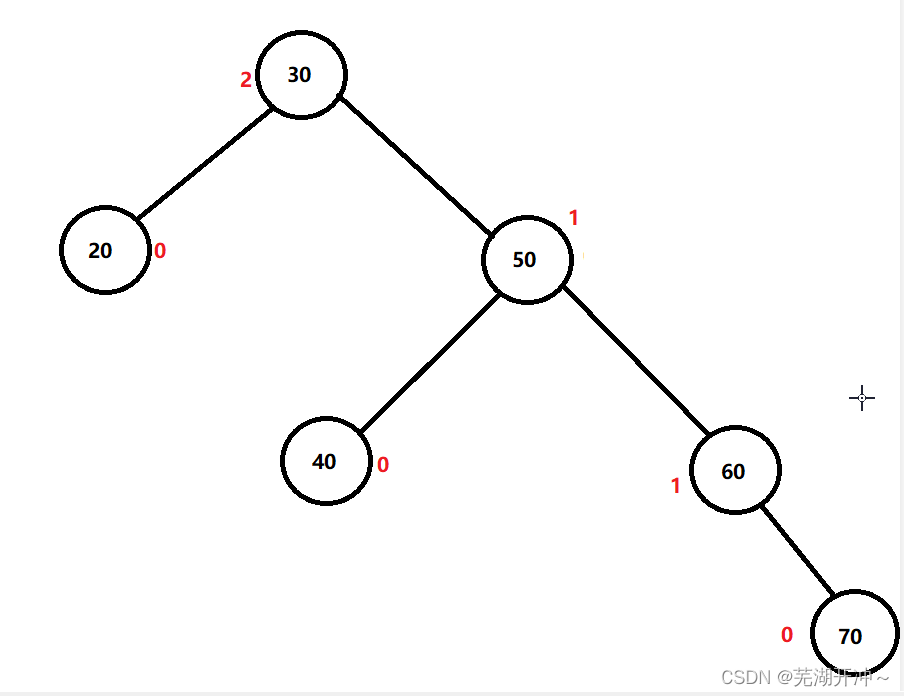
At this time , You can see 30 The equilibrium factor of this node is 2, Do not conform to the AVL Characteristics of trees , So we should adjust this part , For this scenario ( The new node is added to the right test node of the higher right subtree ), We should turn left , The so-called left single rotation , We name the node whose equilibrium factor does not conform to parent, Name its right child subR, And then put parent Set to subR The left child ,subR The original left child ( If any ) Set to parent New right child , If parent If there are parents , Give Way parent Parents point subR Nodes are good , The adjusted picture is shown in the figure
Because of the word balance, we haven't moved for the time being , As can be seen from the picture , The original parent Nodes and subR The balance factor of the node is wrong , Should be changed to 0, So the balance factor of these two nodes will be changed to 0 that will do
Right single spin ( Application : Insert node on the left side of the higher left subtree ) It's wrong with the left single spin , Is to put parent It's just raised on the left child node of , There's nothing to say
Next, let's look at the third case , Right left double rotation ( Application : Insert a node to the left of the higher right subtree )
Listen to the name and you will know how to do it , First right single spin ( Right single spin parent The right child ) Turn left again , Of course , You ask me why I know how to do this ? That was summed up by predecessors , I tried it and found it was right , That's it , You can also try , If you're wrong, you'll make a lot of money
The balance factor may be wrong after two rotations , How to modify it ? Also simple , You try it , In the end, you will find , It is wrong to have only one node at a time
This is the law discovered by others , Of course, there may be more than one
Node* subR = parent->_right;
int bf = subR->_left->_bf;
RotateRight(parent->_right);
RotateLeft(parent);
if (bf == 1) {
parent->_bf = -1;
}
else if (bf == -1) {
subR->_bf = 1;
}The first of the two functions in the middle is right simple rotation , The second is left monocyclone , I think I can draw this , Or remember , There is really nothing to emphasize
Then left and right double rotation ( Application : Insert nodes on the right side of the higher left subtree )
That's right first parent My left child has a left single spin , Right again parent Just one right single spin
Then there is also a node whose balance factor is wrong , You need to adjust it manually
Node* subL = parent->_left;
int bf = subL->_right->_bf;
RotateLeft(parent->_left);
RotateRight(parent);
if (bf == 1) {
subL->_bf = -1;
}
else if (bf == -1) {
parent->_bf = 1;
}Last , Take a look at the overall code , In the middle is the detection of whether the tree is AVL Tree and pre order traversal code
The overall code
template <class T>
class AVLTree {
typedef AVLTreeNode<T> Node;
public:
AVLTree()
:_root(nullptr)
{}
~AVLTree() {
Distory(_root);
}
bool Insert(const T& value) {
// Determine the position to insert
// If AVL The tree is empty.
if (_root == nullptr) {
_root = new Node(value);
return true;
}
// If AVL The tree is not empty
// Find node , Insert it first ;
Node* parent = _root;
Node* child = parent;
while (child) {
parent = child;
if (value > child->_value) {
child = child->_right;
}
else if (value < child->_value) {
child = child->_left;
}
else {
return false;
}
}
child = new Node(value);
child->_parent = parent;
if (child->_value > parent->_value) {
parent->_right = child;
}
else {
parent->_left = child;
}
// Update the balance factor of parents
while (parent) {
//child Insertion will affect the balance factor
if (child == parent->_left) {
parent->_bf--;
}
else {
parent->_bf++;
}
// Judge whether it meets AVL Characteristics of trees
if (parent->_bf == 0) {
break;
}
else if (parent->_bf == 1 || parent->_bf == -1) {
//parent Turn into 1 perhaps -1, It must be right parent Parents also have an impact
child = parent;
parent = parent->_parent;
}
else {
//parent Of _bf Change into 2 perhaps -2, At this time, it needs to be adjusted
if (parent->_bf == 2) {
if (child->_bf == 1) {
RotateLeft(parent);
}
else {
RotateRL(parent);
}
}
else {
if (child->_bf == -1) {
RotateRight(parent);
}
else {
RotateLR(parent);
}
}
break;
}
}
return true;
}
// In the sequence traversal
void InOrder() {
_InOrder(_root);
}
// Judge whether it is AVL Trees
bool IsAVLTree() {
return _IsAVLTree(_root);
}
private:
// Left spin
void RotateLeft(Node* parent) {
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
// Handle subRL node
if (subRL) {
subRL->_parent = parent;
}
// Handle parent node
Node* pparent = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
subR->_parent = pparent;
// Handle parent My parents
if (pparent) {
if (parent == pparent->_left) {
pparent->_left = subR;
}
else {
pparent->_right = subR;
}
}
else { // Before spinning ,parent Root node
_root = subR;
}
// Update equilibrium factor
parent->_bf = subR->_bf = 0;
}
// Right single spin
void RotateRight(Node* parent) {
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
// Handle subLR
if (subLR) {
subLR->_parent = parent;
}
// Handle parent node
Node* pparent = parent->_parent;
parent->_parent = subL;
subL->_right = parent;
subL->_parent = pparent;
// Handle pparent
if (pparent) {
if (parent == pparent->_left) {
pparent->_left = subL;
}
else {
pparent->_right = subL;
}
}
else {
//parent yes root node
_root = subL;
}
// Update equilibrium factor
parent->_bf = subL->_bf = 0;
}
// Right left double rotation
void RotateRL(Node* parent) {
Node* subR = parent->_right;
int bf = subR->_left->_bf;
RotateRight(parent->_right);
RotateLeft(parent);
if (bf == 1) {
parent->_bf = -1;
}
else if (bf == -1) {
subR->_bf = 1;
}
}
// Double left and right
void RotateLR(Node* parent) {
Node* subL = parent->_left;
int bf = subL->_right->_bf;
RotateLeft(parent->_left);
RotateRight(parent);
if (bf == 1) {
subL->_bf = -1;
}
else if (bf == -1) {
parent->_bf = 1;
}
}
// In the sequence traversal
void _InOrder(Node* root) {
if (root == nullptr) {
return;
}
_InOrder(root->_left);
cout << root->_value << " ";
_InOrder(root->_right);
}
// Get the height of the tree
int GetHeight(Node* root) {
if (root == nullptr) {
return 0;
}
return GetHeight(root->_left) > GetHeight(root->_right) ? GetHeight(root->_left) + 1 : GetHeight(root->_right) + 1;
}
// Judge whether it is AVL Trees
bool _IsAVLTree(Node* root) {
if (root == nullptr) {
return true;
}
int high = GetHeight(root->_right) - GetHeight(root->_left);
if (high != root->_bf || abs(high) > 1) {
return false;
}
return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);
}
void Distory(Node*& root) {
if (root) {
Distory(root->_left);
Distory(root->_right);
delete root;
root = nullptr;
}
}
Node* _root;
};
If there is anything you don't understand , Feel free to leave a comment in the comments section , Everyone is on the road , Work together
边栏推荐
- leetcode:面试题 17.24. 子矩阵最大累加和(待研究)
- [dpdk] dpdk sample source code analysis III: dpdk-l3fwd_ 001
- ubuntu20安裝redisjson記錄
- 【knife-4j 快速搭建swagger】
- 大白话高并发(二)
- VHDL implementation of arbitrary size matrix addition operation
- Hisilicon 3559 universal platform construction: RTSP real-time playback support
- 二叉搜索树的实现
- ggplot 分面的细节调整汇总
- About Confidence Intervals
猜你喜欢
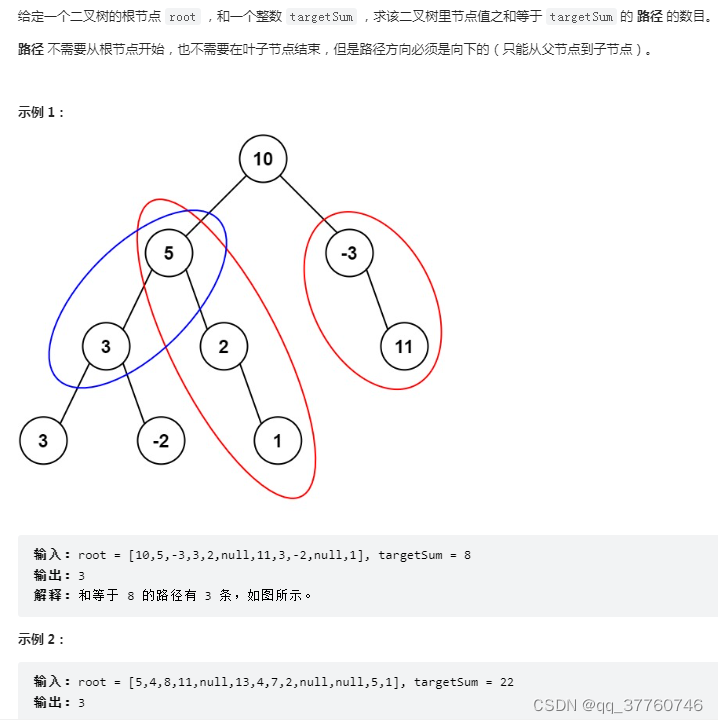
Force buckle ----- path sum III
qt-线程等01概念
SQL injection -day15

【mysql】mysql中行排序
R data analysis: how to predict Cox model and reproduce high score articles
运算放大器应用汇总1

25. (ArcGIS API for JS) ArcGIS API for JS line modification line editing (sketchviewmodel)
【knife-4j 快速搭建swagger】
About Tolerance Intervals
10 ways of interface data security assurance
随机推荐
1.19.11.SQL客户端、启动SQL客户端、执行SQL查询、环境配置文件、重启策略、自定义函数(User-defined Functions)、构造函数参数
Termux set up the computer to connect to the mobile phone. (knock the command quickly), mobile phone termux port 8022
Docker部署Mysql8的实现步骤
枚举通用接口&枚举使用规范
【开发软件】 tilipa开发者软件
10 ways of interface data security assurance
2022夏每日一题(一)
NoSQL之Redis配置与优化
On file uploading of network security
Basic concepts of Huffman tree
22.(arcgis api for js篇)arcgis api for js圆采集(SketchViewModel)
2022年上半年HIT行业TOP50
CMB's written test - quantitative relationship
本机mysql
VHDL implementation of arbitrary size matrix addition operation
一些常用软件相关
About Tolerance Intervals
Create commonly used shortcut icons at the top of the ad interface (menu bar)
Gpt-3 is a peer review online when it has been submitted for its own research
二叉搜索树的实现