当前位置:网站首页>#775 Div.1 B. Integral Array 数学
#775 Div.1 B. Integral Array 数学
2022-07-05 04:43:00 【Strezia】
B
1800
题意
给出一个含 n n n 个数的序列 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,并给出 c c c ,表示序列中所有数大小都不超过 c c c。我们称序列是整的当且仅当对于序列中任意两个(或同一个)数 x , y ( x ≤ y ) x,y(x\leq y) x,y(x≤y) , 满足 ⌊ y x ⌋ \lfloor \frac yx\rfloor ⌊xy⌋ 也在序列中。问这个序列是否是整的。 ( n ≤ 1 e 6 ) (n\leq1e6) (n≤1e6)
思路
这种题第一反应就是用类似素数筛的方法去优化,把对 r = ⌊ y x ⌋ r=\lfloor \frac yx\rfloor r=⌊xy⌋ 的判断改成对 y y y 的判断,不能拆成 x 和 r x和r x和r ”,所以可以枚举所有的 x x x,并枚举所有 r ∉ a r\notin a r∈/a , 如果在 x × r x\times r x×r 对应的范围内存在 y y y,则 r = ⌊ y x ⌋ ∉ a r=\lfloor \frac yx\rfloor\notin a r=⌊xy⌋∈/a ,不是整的。对应的范围即为 [ r × x , r × x + x − 1 ] [r\times x,r\times x + x - 1] [r×x,r×x+x−1],是否存在 y y y 只要预处理前缀和就可以了。
由调和级数,时间复杂度 O ( c log c ) O(c\log c) O(clogc) 。
代码
int cnt[maxn], sum[maxn];
void solve() {
int n, c;
cin >> n >> c;
for(int i = 1; i <= c; i++) cnt[i] = 0;
for(int i = 1; i <= n; i++) {
int x;
cin >> x;
cnt[x]++;
}
sum[0] = 0;
for(int i = 1; i <= c; i++) {
sum[i] = sum[i-1] + cnt[i];
}
for(int x = 1; x <= c; x++) {
if(!cnt[y]) {
continue;
}
for(int i = 1; i * x <= c; i++) {
if(cnt[i]) continue;
int l = i * x - 1;
int r = min((i+1)*x-1, c);
if(sum[r] - sum[l]) {
cout << "No\n";
return;
}
}
}
cout << "Yes\n";
}
边栏推荐
- level18
- Special information | finance, accounting, audit - 22.1.23
- windows下Redis-cluster集群搭建
- [Chongqing Guangdong education] National Open University 2047t commercial bank operation and management reference test in autumn 2018
- 如何进行「小步重构」?
- 可观测|时序数据降采样在Prometheus实践复盘
- Mode in BST (binary tree & Notes on question brushing)
- [Business Research Report] Research Report on male consumption trends in other economic times -- with download link
- [groovy] closure (Introduction to closure class closure | closure parametertypes and maximumnumberofparameters member usage)
- 2021 electrician cup (the 12th "China Society of electrical engineering Cup" National Undergraduate electrician mathematical modeling) detailed ideas + codes + references
猜你喜欢
Cookie learning diary 1

官宣!第三届云原生编程挑战赛正式启动!
![Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 006 unity toolbar](/img/bf/fb4e85143d1461a2026c88cda4a18d.jpg)
Private collection project practice sharing [Yugong series] February 2022 U3D full stack class 006 unity toolbar

2021 huashubei mathematical modeling idea + reference + paper
指针函数(基础)
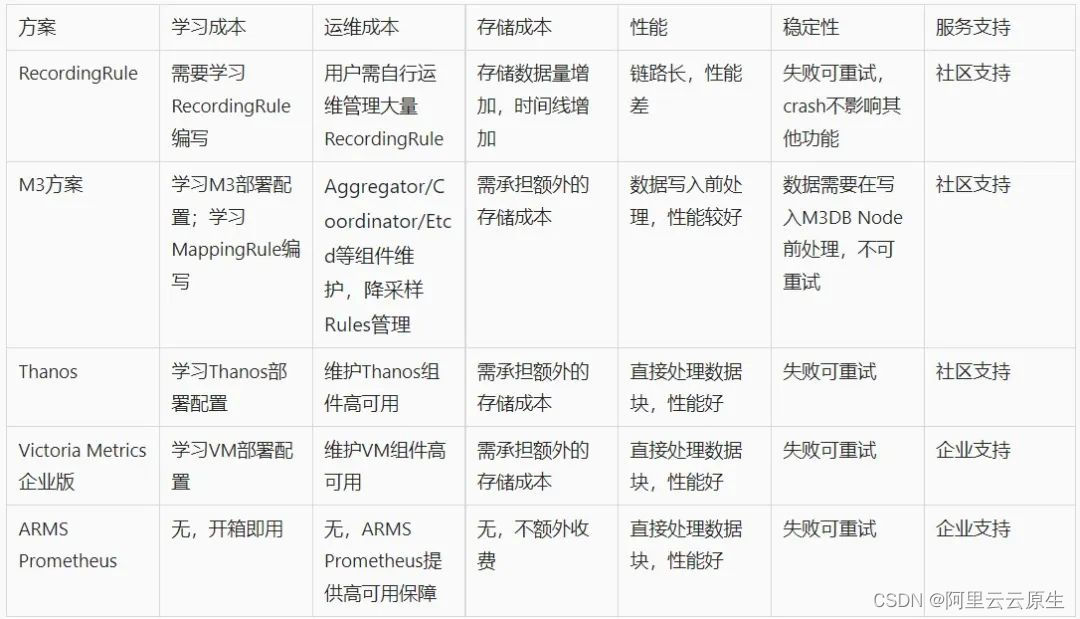
Observable time series data downsampling practice in Prometheus
![[goweb development] Introduction to authentication modes based on cookies, sessions and JWT tokens](/img/20/5c5550e6dabc76702f0e7ce3bef068.jpg)
[goweb development] Introduction to authentication modes based on cookies, sessions and JWT tokens
![[groovy] closure (closure parameter binding | curry function | rcurry function | ncurry function | code example)](/img/90/0cf08ae6fea61891e3e1fdf29d310c.jpg)
[groovy] closure (closure parameter binding | curry function | rcurry function | ncurry function | code example)

计组笔记(1)——校验码、原补码乘除计算、浮点数计算

CSDN正文自动生成目录
随机推荐
Chapter 6 text processing tools for shell programming (awk)
Function (error prone)
[groovy] closure (closure parameter list rule | default parameter list | do not receive parameters | receive custom parameters)
[groovy] closure (closure as function parameter | code example)
Official announcement! The third cloud native programming challenge is officially launched!
Components in protective circuit
函数(基本:参数,返回值)
Leetcode hot topic Hot 100 day 33: "subset"
Reading and visualization of DICOM, MHD and raw files in medical imaging
The 22nd Spring Festival Gala, an immersive stage for the yuan universe to shine into reality
Cookie learning diary 1
You Li takes you to talk about C language 7 (define constants and macros)
The principle of attention mechanism and its application in seq2seq (bahadanau attention)
[goweb development] Introduction to authentication modes based on cookies, sessions and JWT tokens
Web开发人员应该养成的10个编程习惯
Is there a sudden failure on the line? How to make emergency diagnosis, troubleshooting and recovery
Practice | mobile end practice
Setting up redis cluster cluster under Windows
How should programmers learn mathematics
[ideas] 2021 may day mathematical modeling competition / May Day mathematical modeling ideas + references + codes