当前位置:网站首页>次小生成树
次小生成树
2022-07-05 04:36:00 【璀璨的秋叶】

.先求最小生成树,然后依次枚举非树边,然后将该边加入树中,同时从树中去掉一条边,使得最终图仍然是一棵树,统计最小值。
这个方法一定可以找到非严。证明如下
定义1:设T为图G的一棵生成树,对于非树边a和树边b,插入边a,并删除边b的操作记为(+a, -b)。如果T+a-b之后,仍然是一棵生成树,称(+a,-b)是T的一个可行交换。
定义2:称由T进行一次可行变换所得到的新的生成树集合称为T的邻集。
做法中的枚举外部边,删除树中边就是枚举MGT的邻集。
定理:次小生成树一定在最小生成树的邻集中
定理证明:
反证,如果有次小生成树与最小生成树不相同的有k条边,排序做kruskal,找到第一条和次小不同的边,在树中的边t连接ab。
我们将次小中连接ab中的一条边p去掉换成t,那么次小就会变得更小(因为排序kruskal)这样一个可行交换我们让次小生成树和最小生成树的不相同的边数k-1。这种操作可以持续做下去直到只差1条边。所以次小生成树一定在最小生成树的邻集中。
// 新生成树 newsum = sum - w(树内 2 点 之间的边) + w(树外 2 点之间的边)
//(1) 若 newsum < sum (则 sum 一定不是最小生成树边权和 矛盾)
// 所以 sum > newsum (严格次小生成树)
//(2) 若 w(树外 2 点之间的边) (a - b两点剑)不是最大的 那么 最小生成树 一定可以取到这条边
// 矛盾
// 所以 一定要取到 两点之间最大的边 来 替换新边
// 若新边 == 两点之间最大的边 则 取次大
```
#include <bits/stdc++.h>
using namespace std;
#define io std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define x first
#define y second
#define fr front
#define db double
//int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
//int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
//int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
//int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
//int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
typedef pair<int, int> PII;
typedef long long LL ;
const int N = 10010, M = 510;
struct edge
{
int a, b, c, f;
bool operator< (edge x)
{
return c < x.c;
}
}g[N];
int n, m;
int h[M], e[N], w[N], ne[N], idx;// 存储最小生成树
int dist1[M][M], dist2[M][M];// 树中两点的最远距离 与 次远距离
int p[M];
void add(int a, int b, int c) // 添加一条边a->b,边权为c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x) // 并查集
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void dfs(int u, int f, int m1, int m2, int ds1[], int ds2[])
{
ds1[u] = m1, ds2[u] = m2;
for (int i = h[u]; ~i ;i = ne[i])
{
int t = e[i];
if (t != f)
{
int td1 = m1, td2 = m2;
if (w[i] > td1) td2 = td1, td1 = w[i];
else if (w[i] < td1 && w[i] > td2) td2 = w[i];
dfs(t, u, td1, td2, ds1, ds2);
}
}
}
int main()
{
io;
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0;i < m;i ++ )
{
int a, b, c, f = 0;
cin >> a >> b >> c;
g[i] = {a, b, c, f};
}
for (int i = 1;i <= n;i ++ ) p[i] = i;
// 求最小生成树
sort(g, g + m);
LL sum = 0;
for (int i = 0;i < m;i ++ )
{
int a = g[i].a, b = g[i].b, c = g[i].c;
int x = find(a), y = find(b);
if (x != y)
{
add(a, b, c), add(b, a, c); // 存储次小生成树
g[i].f = 1; // 标记在树中
p[x] = y;
sum += c;
}
}
// 新生成树 newsum = sum - w(树内 2 点 之间的边) + w(树外 2 点之间的边)
//(1) 若 newsum < sum (则 sum 一定不是最小生成树边权和 矛盾)
// 所以 sum > newsum (严格次小生成树)
//(2) 若 w(树外 2 点之间的边) (a - b两点剑)不是最大的 那么 最小生成树 一定可以取到这条边
// 矛盾
// 所以 一定要取到 两点之间最大的边 来 替换新边
// 若新边 == 两点之间最大的边 则 取次大
// 求生成树中 两点的最远距离 与 次远距离
for (int i = 1;i <= n;i ++ ) dfs(i, -1, -1e9, -1e9, dist1[i], dist2[i]);
LL ans = 1e18;
for (int i = 0;i < m;i ++ )
if (!g[i].f) // 不止最小生成树里的边
{
int a = g[i].a, b = g[i].b, c = g[i].c;
LL t;
if (c > dist1[a][b])
t = sum + c - dist1[a][b];
else if (c > dist2[a][b])
t = sum + c - dist2[a][b];
ans = min(ans, t);
}
cout << ans << endl;
return 0;
}
边栏推荐
- Learning notes 8
- [phantom engine UE] the difference between running and starting, and the analysis of common problems
- 直播预告 | 容器服务 ACK 弹性预测最佳实践
- Invalid bound statement (not found) in idea -- problem solving
- [uniapp] system hot update implementation ideas
- Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)
- 指针函数(基础)
- [crampon programming] lintcode decoding Encyclopedia - 872 termination process
- 美国5G Open RAN再遭重大挫败,抗衡中国5G技术的图谋已告失败
- 自动语音识别(ASR)研究综述
猜你喜欢
level18

Fuel consumption calculator
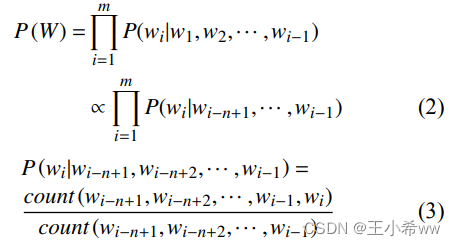
自动语音识别(ASR)研究综述
蛇形矩阵
![[thingsboard] how to replace the homepage logo](/img/65/5296c26f975d79d65d36c2e76e47c1.png)
[thingsboard] how to replace the homepage logo

TPG x AIDU|AI领军人才招募计划进行中!
![[AI bulletin 20220211] the hard core up owner has built a lidar and detailed AI accelerator](/img/cc/06580ce7b553182968d273841a78b4.jpg)
[AI bulletin 20220211] the hard core up owner has built a lidar and detailed AI accelerator

How to get the first few pieces of data of each group gracefully
![[finebi] the process of making custom maps using finebi](/img/3a/d638dbac6a26c37087ec9550c35e63.png)
[finebi] the process of making custom maps using finebi
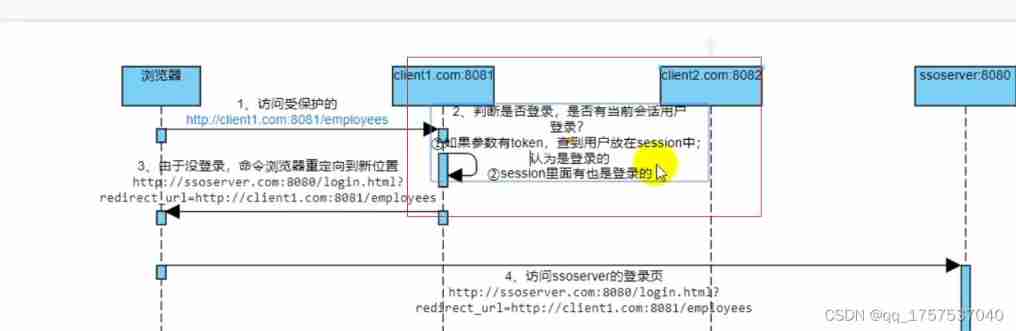
Sequence diagram of single sign on Certification Center
随机推荐
Decryption function calculates "task state and lifecycle management" of asynchronous task capability
Neural network and deep learning Chapter 1: introduction reading questions
Network security - record web vulnerability fixes
[crampon game] MC tutorial - first day of survival
2022-2028 global and Chinese equipment as a Service Market Research Report
Machine learning decision tree
Variable category (automatic, static, register, external)
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
Cookie learning diary 1
Introduction to RT thread kernel (5) -- memory management
OWASP top 10 vulnerability Guide (2021)
Convert Boolean to integer value PHP - Convert Boolean to integer value PHP
【科普】热设计基础知识:5G光器件之散热分析
File upload bypass summary (upload labs 21 customs clearance tutorial attached)
Raki's notes on reading paper: code and named entity recognition in stackoverflow
Managed service network: application architecture evolution in the cloud native Era
MacBook installation postgresql+postgis
美国5G Open RAN再遭重大挫败,抗衡中国5G技术的图谋已告失败
机器学习 --- 神经网络
Sequence diagram of single sign on Certification Center