当前位置:网站首页>假设检验——《概率论与数理统计》第八章学习笔记
假设检验——《概率论与数理统计》第八章学习笔记
2022-07-05 04:17:00 【物联黄同学】
假设检验——《概率论与数理统计》第八章学习笔记
文章目录
前言
感谢台风暹芭,让我回不去宿舍,被迫在实验室过夜,思来想去,睡不着,恰逢期末考临近,决定写一篇的第八章的学习笔记。
和之前的系列一样,教材不变。内容上,选取第八章的前三节,即假设检验,正态均值,正态方差三个部分的知识点,为什么没有其他内容,因为这次考试大概不会考。
形式上,相比前面的章节写了很多课本的定义,这次我会有更多的个人理解,尽可能直击考点。
MindMap
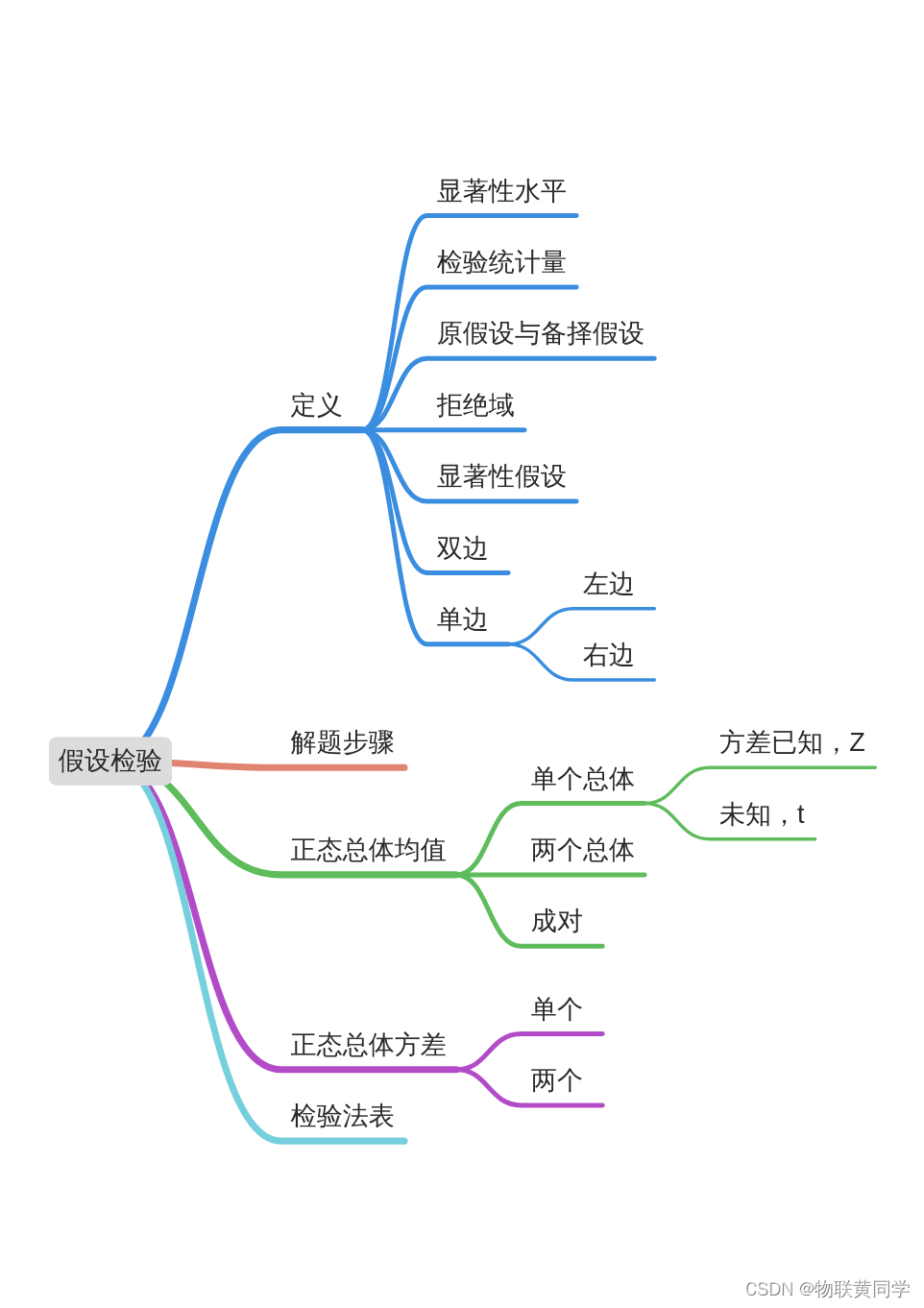
假设检验
这一节其实就是告诉你假设检验的一些定义,以及对假设检验这一问题的解决过程与步骤。
一些定义
显著性水平
我们用来对检验做衡量的标准,一般在式子中以 α出现。
检验统计量
Z = X ‾ − μ 0 σ / n Z = \frac{\overline{X} - \mu_0}{\sigma/\sqrt n} Z=σ/nX−μ0
原假设 与 备择假设
我们将检验问题叙述成:在显著性水平α下,检验假设:
H 0 : μ = μ 0 , H 1 : μ ≠ μ 0 H_0:\mu =\mu_0, \qquad H_1 : \mu \neq \mu_0 H0:μ=μ0,H1:μ=μ0
H0 为 原假设, H1 为 备择假设。
拒绝域
就是在某个区域上取值作为 检验统计量的值时,拒绝 原假设,或者说接受备择假设,这个区域就是拒绝域,而拒绝域的边界点其实就叫 临界点。
显著性检验
因为检验的依据是样本,所以检验势必会有犯错的可能,这里主要有两种错误:
- H0为真,但是拒绝。
- H1为真,但是接受原假设。
我们显然希望犯这两种错误的概率都小,但是在数理统计中,如果样本容量限定了,则减小犯一类错误的概率减小的同时,另一类的概率往往增大。所以在数理统计中,采取的是对第一类控制,不考虑 第二类。这种检验就是 假设性检验。
双边检验与单边检验
这里其实就是我们在做假设的时候,对于H1,μ可能大于μ0,有可能小于μ0,如果是两种都可能,那就是 双边假设, 而如果只是其中一种可能,那就是 单边假设,根据方向又可以分为 左边检验 和 右边检验。对于方向,我的个人理解是看 拒绝域或者备择假设的方向。
个人理解的解题步骤
通过阅读与理解课本的例题,发现了假设检验问题的求解过程:
- 先根据题目确定检验假设。
- 根据参数确定检验统计量。
- 然后根据假设和检验统计量判断是那种假设,然后确定拒绝域。
- 取样,其实就是根据样本观察值判断是否接受原假设。
本篇中所有的总体都是正态总体,针对它的两个参数,均值μ和方差σ^2,有以下两种假设检验。
正态总体均值的假设检验
单个总体
这里根据方差是否已知,又可以分为 Z检验 和 t检验。
方差已知,Z检验
其实很简单,我们根据假设然后接下来需要检验样本均值是否符合假设,在显著性水平α以及其他参数下,检验统计量为:
Z = X ‾ − μ 0 σ / n Z ∼ N ( μ , σ 2 ) Z = \frac{\overline{X} - \mu_0}{\sigma/\sqrt n} \\ Z \sim N(\mu, \sigma^2) Z=σ/nX−μ0Z∼N(μ,σ2)
接下来只需根据是单边假设还是双边假设来求解就可以了。
双边就取α/2,检验统计量的绝对值高于 显著性水平下对应的 正态函数值就拒绝原假设。
方差未知,t检验
这里其实就是 用了样本方差s 来近似替换 总体方差σ,当然这里需要用到t分布。
X ‾ − μ 0 S / n ∼ t ( n − 1 ) \frac{\overline{X} - \mu_0}{S/\sqrt n} \sim t(n-1) S/nX−μ0∼t(n−1)
两个总体——t检验
我们对两个独立的正态总体
N ( μ 1 , σ 2 ) , N ( μ 2 , σ 2 ) N(\mu_1, \sigma^2), N(\mu_2, \sigma^2) N(μ1,σ2),N(μ2,σ2)
方差相同,均值不同,所以可以剔除检验假设:
H 0 : μ 1 − μ 2 = δ , H 1 : μ 1 − μ 2 ≠ δ H_0: \mu_1 - \mu_2 = \delta, \quad H_1:\mu_1 - \mu_2 \neq \delta H0:μ1−μ2=δ,H1:μ1−μ2=δ
所以给出检验统计量:
t = ( X ‾ − Y ‾ ) − δ S w 1 n 1 + 1 n 2 S w 2 = ( n 1 − 1 ) S 1 2 + ( n 2 − 1 ) S 2 2 n 1 n 2 − 2 t= \frac{(\overline{X} - \overline{Y})- \delta}{S_w\sqrt{\frac1{n_1} + \frac 1{n_2}}} \\ S_w^2 = \frac{(n_1 - 1)S_1^2 + (n_2 - 1)S^2_2}{n_1 n_2 - 2} t=Swn11+n21(X−Y)−δSw2=n1n2−2(n1−1)S12+(n2−1)S22
成对数据的检验——t检验
其实这里就是将两组数据对比求差异,然后做检验,我们一般是直接将数据相减后作为一个新的正态总体样本,接下来其实就是单个总体下的情况了。
正态总体方差的假设检验
单个总体
在均值中,我们用到的是Z和t检验,说白了就是用到正态分布和 t分布, 但是在求方差的假设检验的时候,其实用到的是
( n − 1 ) S 2 σ 0 2 ∼ χ 2 ( n − 1 ) \frac{(n-1)S^2}{\sigma_0^2} \sim \chi^2(n - 1) σ02(n−1)S2∼χ2(n−1)
两个总体
用到的是F分布
S 1 2 / S 2 2 σ 1 2 / σ 2 2 ∼ F ( n 1 − 1 , n 2 − 1 ) \frac{S_1^2/ S_2^2}{\sigma_1^2/ \sigma_2^2} \sim F(n_1-1, n_2 -1) σ12/σ22S12/S22∼F(n1−1,n2−1)
正态总体的检验法表
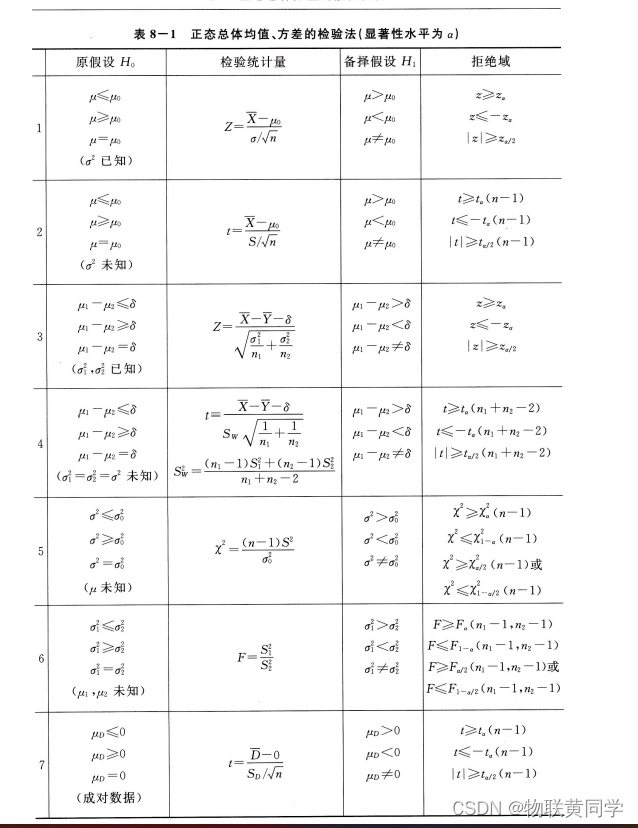
后话
天亮了,回去睡觉了,这一章结合教材阅读会更好一点。
边栏推荐
- As soon as I write the code, President Wang talks with me about the pattern all day
- [untitled]
- 长度为n的入栈顺序的可能出栈顺序
- Common features of ES6
- Summary of scene design
- Use of vscode software
- 行为感知系统
- NetSetMan pro (IP fast switching tool) official Chinese version v5.1.0 | computer IP switching software download
- 3. Package the bottom navigation tabbar
- [uniapp] system hot update implementation ideas
猜你喜欢
C language course setting: cinema ticket selling management system

American 5g open ran suffered another major setback, and its attempt to counter China's 5g technology has failed
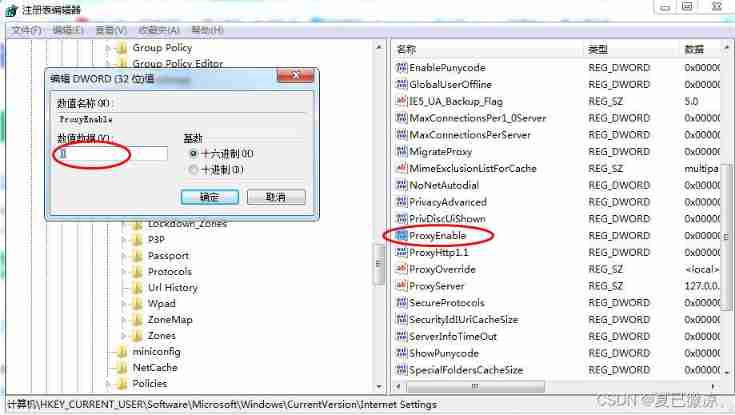
Why can't all browsers on my computer open web pages

Uni app change the default component style

C语言课设:影院售票管理系统
Realize the attention function of the article in the applet
在线文本行固定长度填充工具

【虚幻引擎UE】实现测绘三脚架展开动画制作

Containerd series - what is containerd?

快手、抖音、视频号交战内容付费
随机推荐
快手、抖音、视频号交战内容付费
Threejs realizes rain, snow, overcast, sunny, flame
Threejs Internet of things, 3D visualization of factory
Hexadecimal to octal
A application wakes up B should be a fast method
Convert Boolean to integer value PHP - Convert Boolean to integer value PHP
PR video clip (project packaging)
Behavior perception system
SPI read / write flash principle + complete code
mysql的七种join连接查询
open graph协议
Use threejs to create geometry, dynamically add geometry, delete geometry, and add coordinate axes
Use threejs to create geometry and add materials, lights, shadows, animations, and axes
C语言课设:影院售票管理系统
Moco is not suitable for target detection? MsrA proposes object level comparative learning target detection pre training method SOCO! Performance SOTA! (NeurIPS 2021)...
How to get the first few pieces of data of each group gracefully
ClickPaaS低代码平台
[phantom engine UE] realize the animation production of mapping tripod deployment
As soon as I write the code, President Wang talks with me about the pattern all day
Threejs Internet of things, 3D visualization of farms (I)