Hypothesis testing -- learning notes of Chapter 8 of probability theory and mathematical statistics

Hypothesis testing ——《 Probability theory and mathematical statistics 》 Chapter VIII study notes

Preface

Thanks to typhoon siemba , Let me not go back to the dormitory , Forced to spend the night in the Laboratory , reasoning , Cannot sleep! , Just as the final exam is approaching , Decided to write a study note of Chapter 8 .

Just like the previous series , Teaching materials remain unchanged . Content , Select the first three sections of Chapter 8 , Hypothesis testing , Normal mean , Knowledge points of three parts of normal variance , Why is there nothing else , Because I probably won't take this exam .

Formally , Compared with the previous chapters, many textbook definitions are written , This time I will have more personal understanding , Try to hit the test site directly .

MindMap

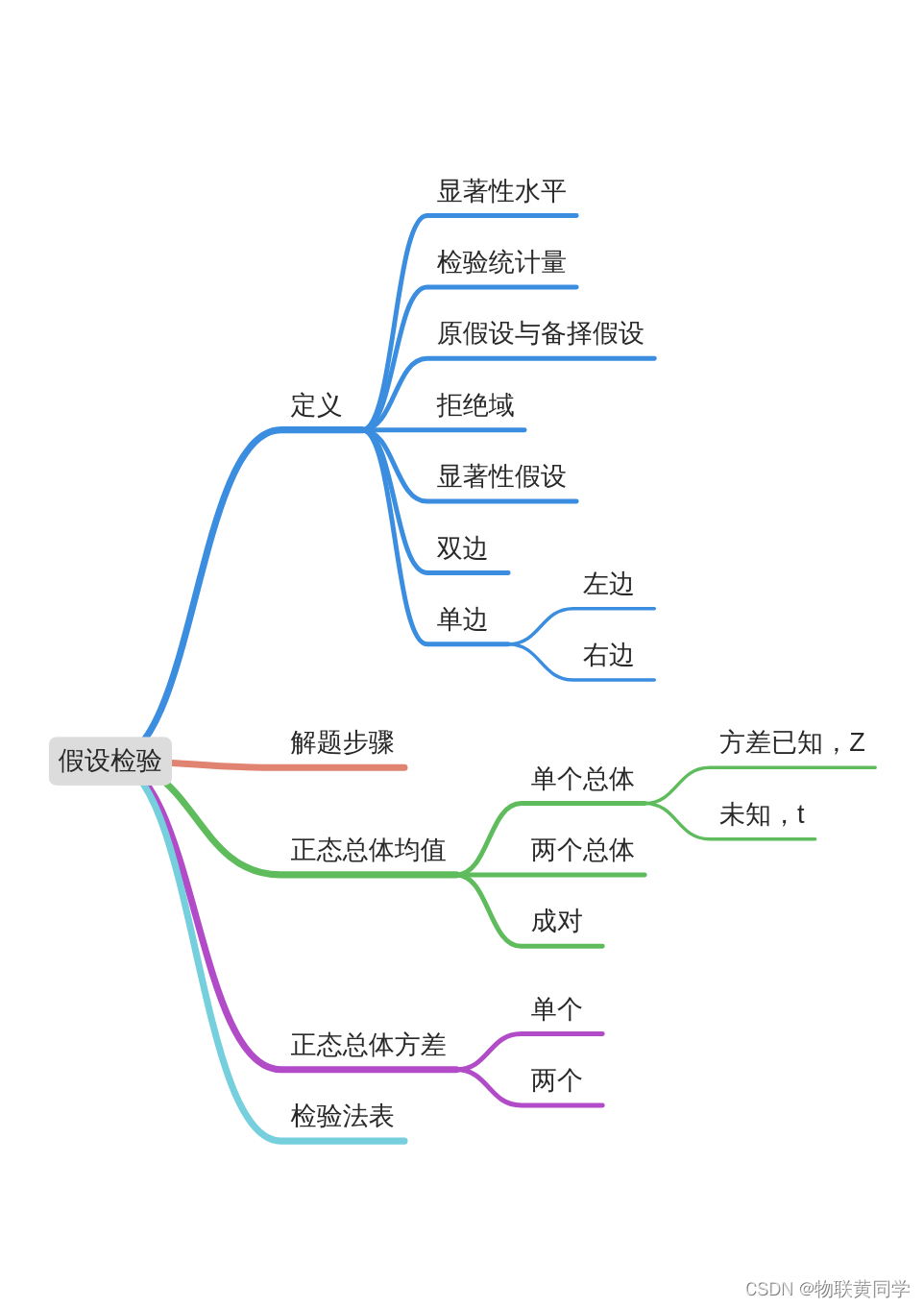
Hypothesis testing

This section actually tells you some definitions of hypothesis testing , And the process and steps of solving the problem of hypothesis testing .

Some definitions

Significance level

The standard we use to measure the inspection , Generally, in the formula α appear .

Test statistic

$$Z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}}$$

The null hypothesis And The alternative hypothesis

We describe the inspection problem as ： At the level of significance α Next , Test the hypothesis ：
$$H_0:\mu ={\mu }_0,H_1:\mu \ne {\mu }_0$$
H0 by The null hypothesis , H1 by The alternative hypothesis .

Reject domain

Is to take a value in a certain area as When testing the value of Statistics , Refuse The null hypothesis , Or accept the alternative hypothesis , This region is the rejection domain , The boundary point of the rejection domain is actually called critical point .

Significance test

Because the test is based on samples , So the test is bound to make mistakes , There are two main mistakes ：

1. H0 It's true , But refuse .
2. H1 It's true , But accept the original hypothesis .

We obviously hope that the probability of making these two kinds of mistakes is small , But in mathematical statistics , If the sample size is limited , While reducing the probability of making a kind of mistake , The probability of the other kind tends to increase . So in mathematical statistics , The first kind of control is adopted , Don't consider The second category . This test is Hypothesis testing .

Bilateral inspection and unilateral inspection

This is actually when we are making assumptions , about H1,μ May be greater than μ0, It may be less than μ0, If it is both possible , That's it Bilateral assumptions , And if it's just one possibility , That's it Unilateral assumptions , According to the direction, it can be divided into Check on the left and Check on the right . For direction , My personal understanding is to see Reject the domain or choose the assumed direction .

Problem solving steps for personal understanding

Through reading and understanding textbook examples , Found the solution process of hypothesis testing problem ：

1. First, determine the test hypothesis according to the topic .
2. Determine the test statistics according to the parameters .
3. Then judge the hypothesis according to the hypothesis and test statistics , Then determine the reject domain .
4. sampling , In fact, it is to judge whether to accept the original hypothesis according to the observed value of the sample .

All the populations in this article are normal populations , For its two parameters , mean value μ And variance σ^2, There are two hypothesis tests .

Hypothesis test of normal population mean

Single population

Here, according to whether the variance is known , Can be divided into Z test and t test .

The variance is known ,Z test

It's very simple , According to the hypothesis, we need to test whether the sample mean meets the hypothesis , At the level of significance α And other parameters , The test statistic is ：
$$\begin{gathered} Z=\frac{\overline{X}-{\mu }_0}{\sigma /\sqrt{n}} \\ Z\sim N(\mu ,{\sigma }^2) \end{gathered}$$
Next, we only need to solve it according to whether it is unilateral hypothesis or bilateral hypothesis .

Take two sides α/2, The absolute value of the test statistic is higher than Corresponding to the significance level The normal function value rejects the original assumption .

The variance is unknown ,t test

This is actually Sample variance is used s To approximate replacement Total variance σ, Of course, we need to use t Distribution .
$$\frac{\overline{X}-{\mu }_0}{S/\sqrt{n}}\sim t(n-1)$$

Two overall ——t test

For two independent normal populations
$$N({\mu }_1,{\sigma }^2),N({\mu }_2,{\sigma }^2)$$
The variance is the same , The mean is different , So we can eliminate the test hypothesis ：
$$H_0:{\mu }_1-{\mu }_2=\delta ,H_1:{\mu }_1-{\mu }_2\ne \delta$$
So give the test statistics ：
$$\begin{gathered} t=\frac{(\overline{X}-\overline{Y})-\delta }{S_w\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \\ {S}_w^2=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1{n}_2-2} \end{gathered}$$

Test of paired data ——t test

In fact, here is to compare the two groups of data to find the difference , Then do the test , We usually subtract the data directly as a new normal population sample , The next step is actually a single overall situation .

Hypothesis test of normal population variance

Single population

In the mean , So here's what we're going to use Z and t test , To put it bluntly, it means using Normal distribution and t Distribution , But in the hypothesis test of variance , In fact, it uses
$$\frac{(n-1)S^2}{{\sigma }_0^2}\sim {\chi }^2(n-1)$$

Two overall

What is used is F Distribution
$$\frac{S_1^2/S_2^2}{{\sigma }_1^2/{\sigma }_2^2}\sim F(n_1-1,n_2-1)$$

Test method table of normal population

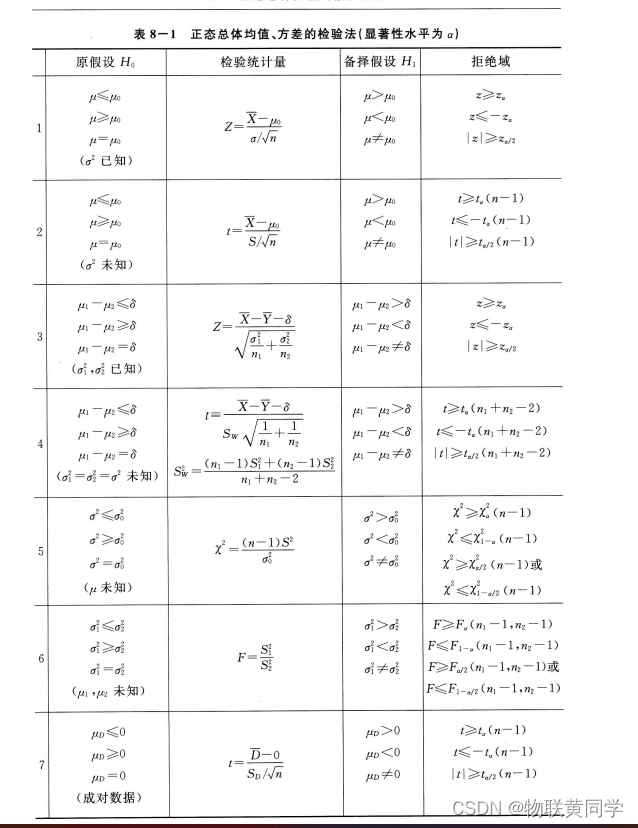
The latter

It's dawn , Go back to bed , This chapter will be better read in combination with the textbook .