当前位置:网站首页>【acwing】528. cheese
【acwing】528. cheese
2022-07-05 04:41:00 【The wind is a little strong】
subject

Ideas
Train of thought
One sentence question : You have to go from the lowest point to the highest point , You must start from the hole connecting with the lower boundary , And you can only walk to the cheese connected with your cheese every time .
For two cheeses , Their distance must be less than 2×r, Is considered to be interlinked .
Two points in space P1(x1,y1,z1)、P2(x2,y2,z2) The formula of distance is as follows :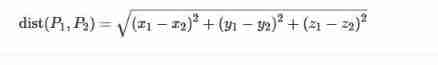
Conditions
The condition of this topic is : Connectivity & Distance formula between two points .
The nature of this topic : Or the connectivity mentioned above . That is, the two cheeses must be connected , Can be transferred
Algorithm to choose : Let's have a preliminary look at this topic , Find it particularly cumbersome , However, in fact, this problem is a maze problem in plane rectangular coordinate system .
For the maze problem , obviously BFS Breadth first search is our best choice .
Analytic algorithm
First of all, for a search topic , We still have three basic goals
Goal one : Direction indicator array : For this topic , Obviously, every hole connected with it can , So the direction of this question indicates that the array is useless .
Goal two : Boundary treatment : For this topic , In fact, there are no requirements for our coordinates , Because connectivity already contains all the conditions .
Goal three : Expand the guidelines : Every search topic , The difficulty often lies in this expansion criterion , This topic is no exception , We found that , The expansion criterion of this topic is the connectivity in the topic , As long as the two points are connected , Then we can expand .
Train of thought two
Obvious , This problem is related to joint search 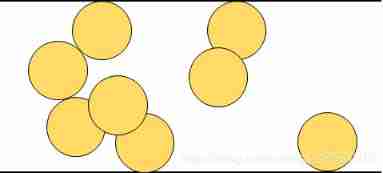
Let's look at the picture above , Do you see some doorways ? We divide all holes into several sets , Once two cavities intersect or tangent , Just put them in the same set .
We can also draw 2 Special elements , Represent bottom and top respectively , If a cavity contacts the bottom , Then put it in the same set as the element representing the bottom , The same is true for the top . Last , Just see if the top and bottom are in the same set . This can be achieved by merging and searching sets .
Idea 1 code
Thought two code
边栏推荐
- Neural networks and deep learning Chapter 2: machine learning overview reading questions
- Sword finger offer 04 Search in two-dimensional array
- English topic assignment (26)
- [Business Research Report] top ten trends of science and technology and it in 2022 - with download link
- Practice | mobile end practice
- Raki's notes on reading paper: code and named entity recognition in stackoverflow
- How to carry out "small step reconstruction"?
- MacBook installation postgresql+postgis
- 线上故障突突突?如何紧急诊断、排查与恢复
- [crampon programming] lintcode decoding Encyclopedia - 1100 strange printer
猜你喜欢
线上故障突突突?如何紧急诊断、排查与恢复
Function (error prone)

American 5g open ran suffered another major setback, and its attempt to counter China's 5g technology has failed

CSDN正文自动生成目录
windows下Redis-cluster集群搭建

官宣!第三届云原生编程挑战赛正式启动!
Label exchange experiment
Sword finger offer 04 Search in two-dimensional array
Flutter 小技巧之 ListView 和 PageView 的各种花式嵌套
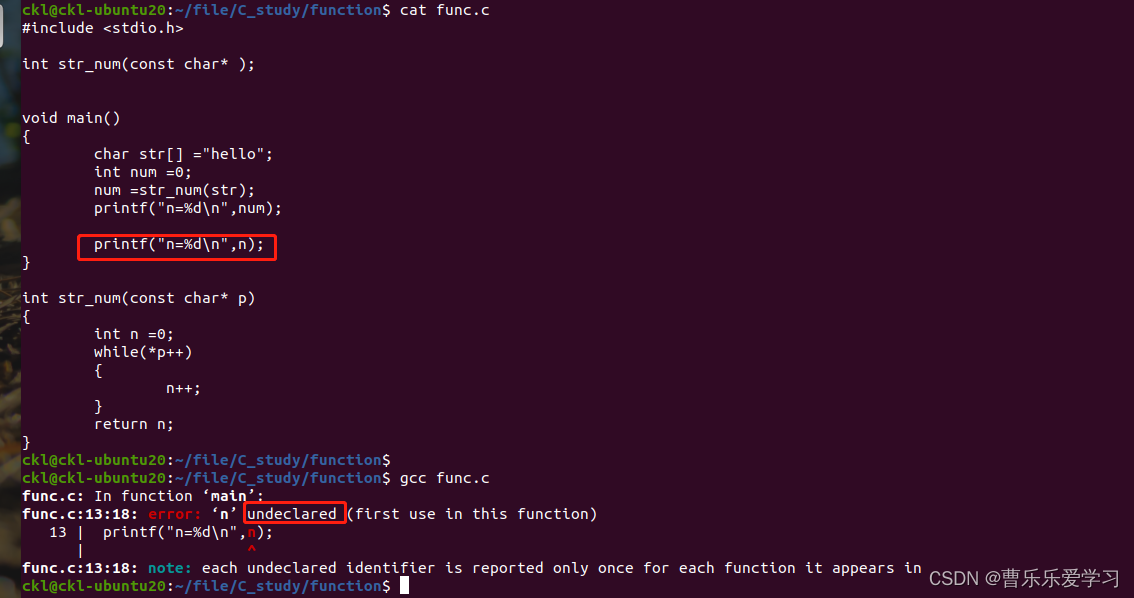
Function (basic: parameter, return value)
随机推荐
Network layer - forwarding (IP, ARP, DCHP, ICMP, network layer addressing, network address translation)
Rk3399 platform development series explanation (network debugging) 7.29 summary of network performance tools
Introduction to RT thread kernel (5) -- memory management
Uncover the seven quirky brain circuits necessary for technology leaders
Thematic information | carbon, carbon neutrality, low carbon, carbon emissions - 22.1.9
Data security -- 14 -- Analysis of privacy protection governance
Fonction (sujette aux erreurs)
Observable time series data downsampling practice in Prometheus
[illusory engine UE] method to realize close-range rotation of operating objects under fuzzy background and pit recording
Matplotlib draws three-dimensional scatter and surface graphs
Machine learning decision tree
Error statuslogger log4j2 could not find a logging implementation
A solution to the problem that variables cannot change dynamically when debugging in keil5
[Chongqing Guangdong education] National Open University 2047t commercial bank operation and management reference test in autumn 2018
Basic analysis of IIC SPI protocol
2022-2028 global and Chinese virtual data storage Market Research Report
Special information | finance, accounting, audit - 22.1.23
About the prompt loading after appscan is opened: guilogic, it keeps loading and gets stuck. My personal solution. (it may be the first solution available in the whole network at present)
可观测|时序数据降采样在Prometheus实践复盘
Here comes the Lantern Festival red envelope!