Introduce Hamming distance and calculation examples

Hamming distance (Hamming distance) It is to calculate the sum of the number of different corresponding elements between two vectors . In this paper, R、Python The calculation process of language .

Overview of Hamming distance

Hamming distance is based on American mathematician Richard · It's named after Han Ming , He was in 1950 The example measurement index was proposed in the paper on Hamming code in . It is widely used in many disciplines , Such as information theory 、 Coding theory and cryptography .

give an example ：
“karolin” and “kathrin” The Hamming distance between two strings is s 3 ( The difference characters are : r-t, o-h, l-r),

1011100 and 1001000 The distance between Han and Ming is 2 ( Different binary numbers are : 1-0 and 1-0)

31738 and 32337 The distance between Han and Ming is 3 ( Different integer digits : 1-2, 7-3, and 8-7).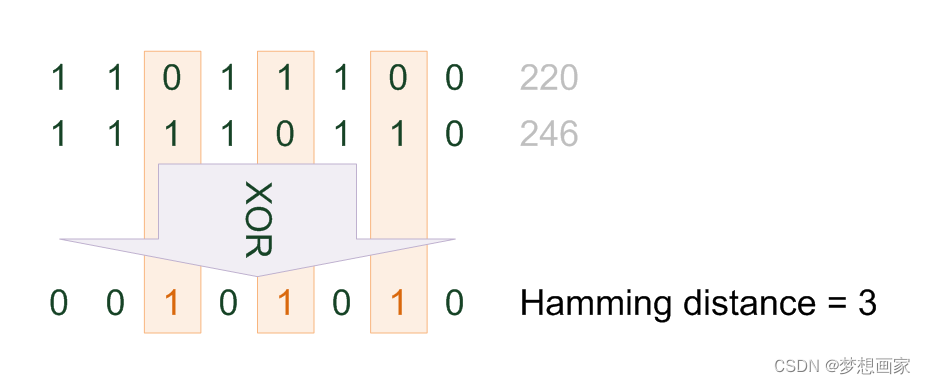

Hamming distance has proved to be very useful in solving many problems . for example , In coding theory, it is used for error detection and error correction codes ; In genetics, it is used to measure genetic differences ; Used to find similarities or differences in machine learning algorithms .

Implementation function

Suppose you have two vectors x = [1, 2, 3, 4] ;y = [1, 2, 5, 7] .
The Hamming distance between them is 2, Because the last two corresponding elements are different .

R The computational logic of the language is ：

sum(x != y)

Python The calculation process of is ：

#  Custom function implementation 
def hammingDistance(s1, s2):
    """ Returns the Hamming distance between equal length sequences """
    if len(s1) != len(s2):
        raise ValueError("Undefined for sequences of unequal length")
    return sum(el1 != el2 for el1, el2 in zip(s1, s2))

You can also use it scipy.spatial.distance package hamming The function calculates directly .

Example 1( Binary type )

The following example calculates the distance between two including binary vectors ：

# R Language implementation 
#  Create a vector 
x <- c(0, 0, 1, 1, 1)
y <- c(0, 1, 1, 1, 0)
sum(x != y)

# [1] 2

Python Code implementation ：

from scipy.spatial.distance import hamming

x = [0, 1, 1, 1, 0, 1]
y = [0, 0, 1, 1, 0, 0]

hamming(x, y) * len(x)

# 2.0

Example 2( value type )

Hamming distance of numeric type vector ：

#  Create a vector 
x <- c(7, 12, 14, 19, 22)
y <- c(7, 12, 16, 26, 27)

#  Calculate Hamming distance 
sum(x != y)

# [1] 3

Python Code implementation ：

from scipy.spatial.distance import hamming

x = [7, 12, 14, 19, 22]
y = [7, 12, 16, 26, 27]

hamming(x, y) * len(x)

# 3.0

Example 3( String type )

Calculate Hamming distance of string type ：

#  Create a vector 
x <- c('a', 'b', 'c', 'd')
y <- c('a', 'b', 'c', 'r')

#  Calculate Hamming distance 
sum(x != y)

# [1] 1

Python Language implementation ：

from scipy.spatial.distance import hamming 

#  Define an array 
x = ['a', 'b', 'c', 'd']
y = ['a', 'b', 'c', 'r']

hamming(x, y) * len(x)

# 1.0

summary

This paper introduces the Hamming distance , And introduce through examples R and Python The implementation process of language .