汉诺塔问题思路的证明

前言

问题描述：在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

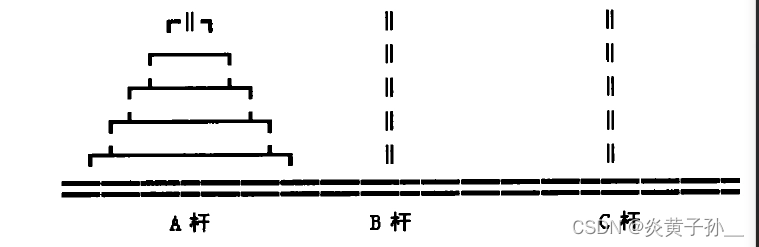
问题分析

其实答案的思路很简单：

• 设A上有n个圆盘
  • 如果n=1，就直接将 A->C ，Move( A, C);
  • 如果是其他情况
    • 先将前 A 上的 n-1 个圆盘移动到 B 上，Hanoi(n - 1, A, C, B)
    • 再将 A 上的最后一个圆盘移动到 C上，Move(A, C)
    • 最后将 B 上的 n-1 个圆盘移动的 C 上，Hanoi(n - 1, B, A, C)

但为什么这样可行？这个比较让人费解。这里我给大家提供一个思路：利用数学归纳法。
证:
假设 f(n) 操作代表把 n 个圆盘从 A 杆移动到 C 杆
注意，将 n 个圆盘无论是进行 A->C、B->C、A->B、C->B，B->A、C->A，这几个操作是完全等价的

首先，f(1) 操作一定可行
现假设 f(n) 操作可行，则 f(n+1) 操作代表要把 n+1 个圆盘从 A 杆移动到 C 杆。

因为 f(n) 操作可行，所以可以把 n 个圆盘从 A 杆移动到 B 杆，将 A 杆剩余的最后一个圆盘直接放到 C 杆。
然后还是因为 f(n) 可行，所以可以直接把 B 杆的 n 个圆盘移动到 C 杆
由此可知 f(n+1) 的操作可行。

得证：当 n∈{1,2,3,…} 时, f(n) 操作可行

下面是C语言版完整的案例，P121_6 代表题号，这个代码是我刷题的时候写的。起始真正的操作只有 P121_6 这一个函数，其他函数都是用于输出相关信息的，方便我们观察究竟发生了什么。

typedef struct {
    
       int *A;
       int *B;
       int *C;
       int top[3];
}s_Hannoi,*p_hannoi;

// 汉诺塔堆栈初始化
void P121_6_init(s_Hannoi& h, int n)
{
    
       int i = n-1;
       h.A = (int*)malloc(sizeof(int) * n);
       h.B = (int*)malloc(sizeof(int) * n);
       h.C = (int*)malloc(sizeof(int) * n);
       h.top[0] = i;
       h.top[1] = -1;
       h.top[2] = -1;
       for (;i >= 0;i--) {
    
              h.A[i] = i;
       }
}

void P121_6_Move(s_Hannoi& h,char out,char in)
{
    
       int temp = -1,i,j;
       printf("%c->%c:\n", out, in);
       switch (out) {
    
       case 'A': 
              temp = h.A[h.top[0]];
              --h.top[0];
              break;
       case 'B':
              temp = h.B[h.top[1]];
              --h.top[1];
              break;
       case 'C':
              temp = h.C[h.top[2]];
              --h.top[2];
              break;
       }
       switch (in) {
    
       case 'A':
              ++h.top[0];
              h.A[h.top[0]] = temp;
              break;
       case 'B':
              ++h.top[1];
              h.B[h.top[1]] = temp;;
              break;
       case 'C':
              ++h.top[2];
              h.C[h.top[2]] = temp;
              break;
       }
       // 打印当前结构
       printf("\tA:");
       for (i = 0;i < h.top[0]+1;i++) {
    
              printf("%d,", h.A[i]);
       }
       printf("\n\tB:");
       for (i = 0;i < h.top[1]+1;i++) {
    
              printf("%d,", h.B[i]);
       }
       printf("\n\tC:");
       for (i = 0;i < h.top[2]+1;i++) {
    
              printf("%d,", h.C[i]);
       }
       printf("\n");
}

// 汉诺塔问题
void P121_6(s_Hannoi& h,int n,char A,char B,char C)
{
    
       if (n == 1) {
    
              P121_6_Move(h, A, C);
       }
       else {
    
              P121_6(h, n - 1, A, C, B);
              P121_6_Move(h, A, C);
              P121_6(h, n - 1, B, A, C);
       }
}

int main()
{
    
       printf("***********************\n");
       s_Hannoi h;
       P121_6_init(h, 6);
       P121_6(h, 6, 'A', 'B', 'C');
}