Some opinions and code implementation of Siou loss: more powerful learning for bounding box regression zhora gevorgyan

Recently, many official account are pushing this article , But I have some problems in the process of reading , Because the code is not open source , Understanding may not be correct , So first record , After open source, we can understand it more deeply compared with the code , I also hope that if some big guys see this article , Can you give me some advice on my immature views .
The final loss function of the experiment is calculated as follows ：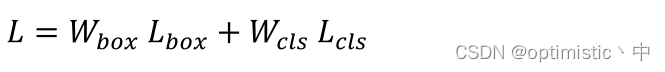

among $L_{cls}$ It is used. focal loss,$W_{box}$ and $W_{cls}$ The weight parameters are calculated according to genetic algorithm ,$L_{box}$ It is what this article mentions SIoU Loss , The calculation is as follows ：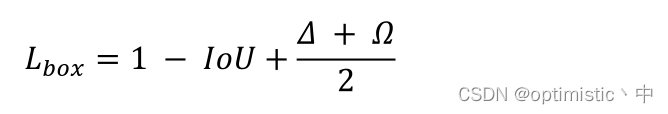

It mainly involves four parts of losses ： Angle loss 、 Distance loss 、 Shape loss 、IoU Loss
1. Angle loss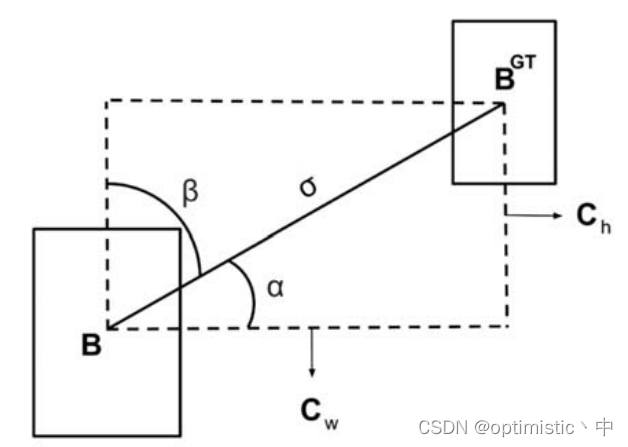

Here the author thinks , Angle factor can be considered , First, make the prediction box return to the same horizontal line or vertical line as the truth box , I agree with that , Can accelerate convergence , The author evaluates the loss through the following formula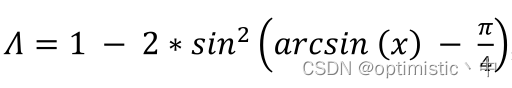

The formula consists of two parts , The first part is $1-2si{n}^2(x)$, In fact, it is $cos(2x)$, Make the $x>0$ The situation of , Its value is only in $x$ by $\pi /4$ Take the minimum when , obtain 0, And in the $x$ by 0 Take the maximum when , obtain 1; The second part is $arcsin(x)-\pi /4$, among $arcsin(x)$ That is to say $\alpha$, It needs to be done $-\pi /4$ The operation of is to consider moving the prediction box towards the side with a smaller angle , because $\beta$ be equal to $\pi /2-\alpha$, both $-\pi /4$ The latter numbers are opposite to each other , after $cos$ The calculated value of the function is the same , When $\alpha$ by 0 When , Its loss is the smallest , But for $\pi /4$ It's the biggest when I'm young . Finally, the prediction box moves faster to the horizontal or vertical line where the truth box is located .
2. Distance loss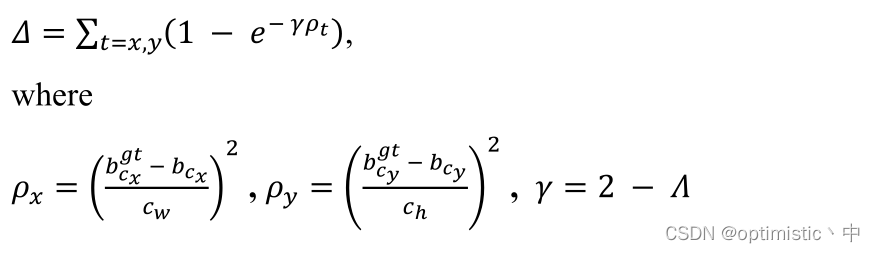

（1） about ${\rho }_x$ and ${\rho }_y$ The calculation of , I was still thinking that this would not always calculate the identity 1 Do you , Then I found the figure in the paper 3 The diagram is given , there $c_w$ and $c_h$ Refers to the length of the smallest external frame .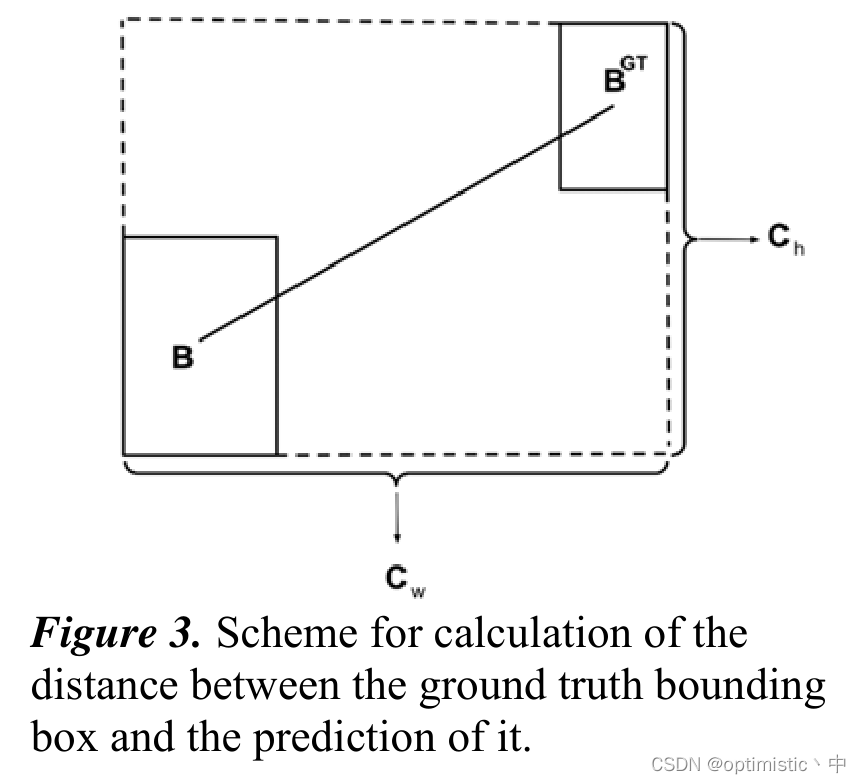

（2） about $\gamma$ Calculation method of , My understanding is that first of all, we can get $\Lambda$ The scope of should be [0,1], Here we pass $2-\Lambda$, First, prevent $\gamma$ by 0 when ${\rho }_t$ Failure situation , Secondly, make $\Lambda$ The smaller it is ,${\rho }_t$ The greater the impact of change on losses .
3. Shape loss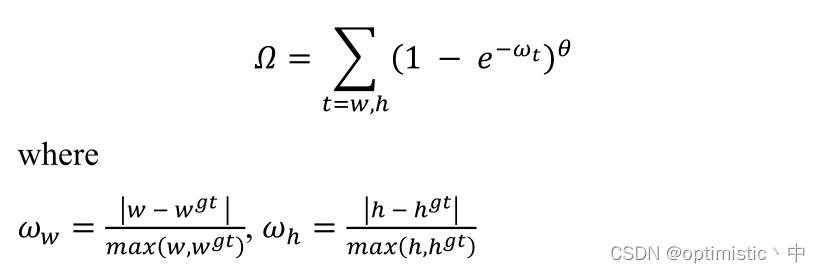

Here and EIOU equally , Both take into account the true aspect ratio between the prediction box and the truth box , But for the ${\omega }_x$ and ${\omega }_y$ The calculation of , And EIOU We also need to calculate that the minimum frame length and width that can surround two frames are different , Only the length and width attributes of the truth box and the prediction box are used here , Less computation , It's supposed to be faster , But the specific effect is not clear . in addition ,${\omega }_t$ The range is [0,1], I don't think it is necessary to pass $1-e^{-{\omega }_t}$ Further calculation , Maybe the effect will be better , Finally, for $\theta$ The introduction of , It's not very understandable here .
（1） First of all, I don't understand why it would be better to introduce this factor .
（2） Secondly, distance loss can also introduce factors , Why not introduce .
4.IoU Loss
and GIOU The same as mentioned in , Here is the press $1-IoU$ To calculate the
For some weights and in the article $\theta$ Parameters are calculated by genetic algorithm on the data set , I don't know the improvement effect of this part , Because the code is not open source , There are also doubts about some of these calculation methods , Therefore, it is impossible to verify the real effect of each improvement point

Here's my comment on SIoU A simple reproduction of , If there is any mistake, please correct it

#(x1,y1) and (x2,y2) They are the central coordinates of the prediction box and the real box 
x1 = (b1_x1 + b1_x2) / 2
x2 = (b2_x1 + b2_x2) / 2
y1 = (b1_y1 + b1_y2) / 2
y2 = (b2_y1 + b2_y2) / 2
x_dis = torch.max(x1, x2) - torch.min(x1, x2)
y_dis = torch.max(y1, y2) - torch.min(y1, y2)
sigma = torch.pow(x_dis ** 2 + y_dis ** 2, 0.5) + eps
alpha = y_dis / sigma
beta = x_dis / sigma
threshold = pow(2, 0.5) / 2
sin_alpha = torch.where(alpha > threshold, beta, alpha)
#1 - 2 * sin(x) ** 2  Equate to cos(2x)
angle_cost = torch.cos(torch.arcsin(sin_alpha) * 2 - np.pi / 2)
cw += eps
ch += eps
rho_x = (x_dis / cw) ** 2
rho_y = (y_dis / ch) ** 2
gamma = 2 - angle_cost
distance_cost = 2 - torch.exp(-1 * gamma * rho_x) - torch.exp(-1 * gamma * rho_y)
omiga_w = torch.abs(w1 - w2) / (torch.max(w1, w2) + eps)
omiga_h = torch.abs(h1 - h2) / (torch.max(h1, h2) + eps)
#  In the original paper theta stay 4 near , Range 2 To 6
theta = 4
shape_cost = torch.pow(1 - torch.exp(-1 * omiga_w), theta) + torch.pow(1 - torch.exp(-1 * omiga_h), theta)
return iou - 0.5 * (distance_cost + shape_cost)