当前位置:网站首页>[AGC009D]Uninity
[AGC009D]Uninity
2022-07-06 11:17:00 【OneInDark】
subject
Ideas
For me , Super big problem , No idea at all ; Yes H I D \sf HID HID Come on , Garbage water problem , Make it casually .
The topic is preliminarily transformed : Build a class point tree , Minimize the height . If you build from top to bottom , There is a conclusion a n s ∈ { k , k + 1 } ans\in\{k,\;k{\rm+}1\} ans∈{ k,k+1}, However, it is completely useless . You can also consider the adjustment method of finding the center of gravity —— Obviously not. .
I thought again Bottom up Build up trees . The leaves of the original tree , There must be leaves on the dianfen tree . therefore , Adjacent to the leaves of the original tree , It is the penultimate layer of the dot tree . But further up ? I feel , If it could be 1 1 1 That's it 1 1 1 . Or license ; What about going up ? Because it is not formalized , I finally failed .
What to do in this topic , Namely Write the above thinking into a theorem . So it's the conclusion again, right . Only from the perspective of the above visual description , It's hard to clarify something .
Theorem : set up f : V ↦ N f:V\mapsto\N f:V↦N, That is, label each dot , Satisfy for any f ( x ) = f ( y ) ( x ≠ y ) f(x)=f(y)\;(x\ne y) f(x)=f(y)(x=y), There is z ∈ path ( x , y ) z\in\text{path}(x,y) z∈path(x,y) bring f ( z ) > f ( x ) f(z)>f(x) f(z)>f(x), remember v ( f ) = max f ( x ) v(f)=\max f(x) v(f)=maxf(x), The answer is min v ( f ) \min v(f) minv(f) .
Obviously, any legal solution corresponds to such a f f f . Next, just prove , In this way f f f In turn, a set of solutions can be constructed , And the answer of this solution does not exceed v ( f ) v(f) v(f) . Using induction , A point is obviously true ; When there are multiple points , find max f ( x ) \max f(x) maxf(x), Obviously this is the only . Take it as the root of the pointwise tree , Induction is applied to each connected block , The answer is no more than v ( f ′ ) ⩽ v ( f ) − 1 v(f')\leqslant v(f)-1 v(f′)⩽v(f)−1, So the answer of this plan does not exceed v ( f ′ ) + 1 ⩽ v ( f ) v(f')+1\leqslant v(f) v(f′)+1⩽v(f), Certificate completion .
then , We can Greedy recursive processing . Its source , Is the idea of building from the bottom up , But here we can give a more concise 、 More formal proof . set up y < f ( x ) y<f(x) y<f(x), If order f ( x ) = y f(x)=y f(x)=y after x x x The subtree of is still a legal point tree ( When only the points in the subtree are considered , Satisfying the theorem f f f mapping ), set up z z z by x x x Father in the tree , Then order again f ( z ) = max [ f ( z ) , f ( x ) ] f(z)=\max[f(z),f(x)] f(z)=max[f(z),f(x)] You can get a new legal point tree ( there f ( x ) f(x) f(x) Is the original mapping value ).
It is easy to verify the legitimacy of the scheme : Across x x x The path of , If you cross z z z It is still legal , because f ( z ) f(z) f(z) No less than the original f ( x ) f(x) f(x); No crossing z z z It is still legal , This is a prerequisite . No crossing x x x The path of , It must still be legal .
and v ( f ) v(f) v(f) It won't change . therefore f ( x ) f(x) f(x) The value of is unique , It just makes the subtree become the minimum value of the legal point tree . that , On the original tree d f s \tt dfs dfs, Store which in each subtree f ( x ) f(x) f(x) It needs to be avoided ( No bigger f f f Put it “ Occlusion ” live ) that will do . in consideration of f ( x ) ⩽ log n f(x)\leqslant\log n f(x)⩽logn, It can be compressed , Time complexity O ( n ) \mathcal O(n) O(n) .
Code
#include <cstdio> // JZM yydJUNK!!!
#include <iostream> // XJX yyds!!!
#include <algorithm> // XYX yydLONELY!!!
#include <cstring> // (the STRONG long for LONELINESS)
#include <cctype> // ZXY yydSISTER!!!
#include <vector>
using namespace std;
# define rep(i,a,b) for(int i=(a); i<=(b); ++i)
# define drep(i,a,b) for(int i=(a); i>=(b); --i)
typedef long long llong;
inline int readint(){
int a = 0, c = getchar(), f = 1;
for(; !isdigit(c); c=getchar())
if(c == '-') f = -f;
for(; isdigit(c); c=getchar())
a = (a<<3)+(a<<1)+(c^48);
return a*f;
}
inline void getMin(int &x, const int &y){
if(y < x) x = y;
}
const int MAXN = 100005;
struct Edge{
int to, nxt;
Edge() = default;
Edge(int _t, int _n): to(_t), nxt(_n){
}
};
Edge e[MAXN<<1]; int head[MAXN], cntEdge;
void addEdge(int a, int b){
e[cntEdge] = Edge(b,head[a]), head[a] = cntEdge ++;
}
int ans;
int dfs(int x, int pre){
int s = 0, bad = 0;
for(int i=head[x]; ~i; i=e[i].nxt){
if((i^1) == pre) continue;
const int &&ch = dfs(e[i].to,i);
bad |= s&ch, s |= ch;
}
int chose = bad ? 32-__builtin_clz(bad) : 0;
chose += __builtin_ffs((s>>chose)+1)-1;
ans = max(ans,chose); return ((s>>chose)|1)<<chose;
}
int main(){
int n = readint();
memset(head+1,-1,n<<2);
for(int i=1,a,b; i!=n; ++i){
a = readint(), b = readint();
addEdge(a,b), addEdge(b,a);
}
dfs(1,-1); printf("%d\n",ans);
return 0;
}
边栏推荐
- Project practice - background employee information management (add, delete, modify, check, login and exit)
- 导入 SQL 时出现 Invalid default value for ‘create_time‘ 报错解决方法
- Invalid global search in idea/pychar, etc. (win10)
- windows下同时安装mysql5.5和mysql8.0
- Record a problem of raspberry pie DNS resolution failure
- Did you forget to register or load this tag
- neo4j安装教程
- Redis的基础使用
- [Thesis Writing] how to write function description of jsp online examination system
- Software testing and quality learning notes 3 -- white box testing
猜你喜欢
Software testing and quality learning notes 3 -- white box testing
Deoldify项目问题——OMP:Error#15:Initializing libiomp5md.dll,but found libiomp5md.dll already initialized.

LeetCode #461 汉明距离
error C4996: ‘strcpy‘: This function or variable may be unsafe. Consider using strcpy_s instead
Picture coloring project - deoldify

图片上色项目 —— Deoldify
![[C language foundation] 04 judgment and circulation](/img/59/4100971f15a1a9bf3527cbe181d868.jpg)
[C language foundation] 04 judgment and circulation
基于apache-jena的知识问答
Image recognition - pyteseract TesseractNotFoundError: tesseract is not installed or it‘s not in your path
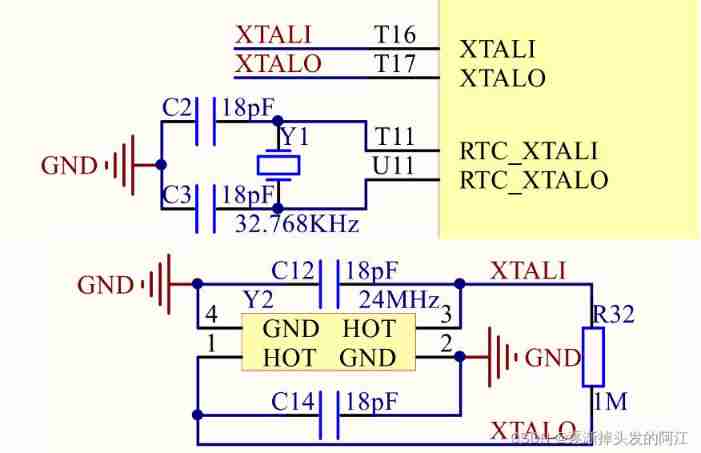
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
随机推荐
Django running error: error loading mysqldb module solution
打开浏览器的同时会在主页外同时打开芒果TV,抖音等网站
Error reporting solution - io UnsupportedOperation: can‘t do nonzero end-relative seeks
In the era of DFI dividends, can TGP become a new benchmark for future DFI?
Knowledge Q & A based on Apache Jena
Install MySQL for Ubuntu 20.04
1. Mx6u learning notes (VII): bare metal development (4) -- master frequency and clock configuration
【博主推荐】asp.net WebService 后台数据API JSON(附源码)
[recommended by bloggers] C WinForm regularly sends email (with source code)
Idea import / export settings file
Principes JDBC
Other new features of mysql18-mysql8
Ansible practical Series II_ Getting started with Playbook
Install mysql5.5 and mysql8.0 under windows at the same time
Redis的基础使用
一键提取pdf中的表格
CSDN question and answer tag skill tree (I) -- Construction of basic framework
QT creator specifies dependencies
@Controller, @service, @repository, @component differences
Classes in C #