当前位置:网站首页>AcWing 1298.曹冲养猪 题解
AcWing 1298.曹冲养猪 题解
2022-07-06 09:14:00 【爱吃章鱼的怪兽】
AcWing 1298 .曹冲养猪 题解
题目描述
自从曹冲搞定了大象以后,曹操就开始琢磨让儿子干些事业,于是派他到中原养猪场养猪,可是曹冲很不高兴,于是在工作中马马虎虎,有一次曹操想知道母猪的数量,于是曹冲想狠狠耍曹操一把。
举个例子,假如有 16 16 16 头母猪,如果建了 3 3 3 个猪圈,剩下 1 1 1 头猪就没有地方安家了;如果建造了 5 5 5 个猪圈,但是仍然有 1 1 1 头猪没有地方去;如果建造了 7 7 7 个猪圈,还有 2 2 2 头没有地方去。
你作为曹总的私人秘书理所当然要将准确的猪数报给曹总,你该怎么办?
输入格式
第一行包含一个整数 n n n,表示建立猪圈的次数;
接下来 n n n 行,每行两个整数 a i , b i a_i,b_i ai,bi表示建立了 a i a_i ai 个猪圈,有 b i b_i bi 头猪没有去处。
你可以假定 a i , a j a_i,a_j ai,aj 互质
输出格式
输出仅包含一个正整数,即为曹冲至少养猪的数目
数据范围
1 ≤ b ≤ 10 1\le b \le 10 1≤b≤10
1 ≤ b i ≤ a i ≤ 1100000 1\le b_i\le a_i\le 1100000 1≤bi≤ai≤1100000
所有 a i a_i ai的乘积不超过 1 0 18 10^{18} 1018
题解
这道题的考点是中国剩余定理
我们将中国剩余描述为如下形式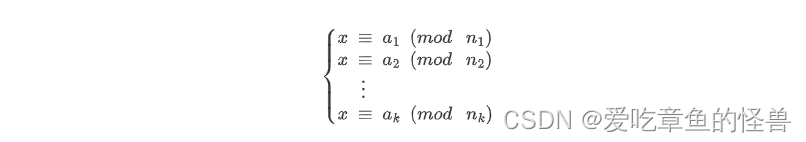
在这里给出计算中国剩余定理的方法并证明
计算所有模数的积 n n n
对于第 i i i 个方程:
a. 计算 m i = n n i m_i=\dfrac{n}{n_i} mi=nin
b. 计算 m i m_i mi 在模 n i n_i ni 意义下的逆元 m i − 1 m_i^{-1} mi−1
c. 计算 c i = m i × m i − 1 c_i =m_i\times m_i^{-1} ci=mi×mi−1 (不对 n i n_i ni 取模)
方程组的唯一解为: x = ∑ i = 1 k a i c i ( m o d n i ) x=\sum^k_{i=1}a_i~c_i (mod ~n_i) x=∑i=1kai ci(mod ni)
证明:
我们可以证明用这种方法得到的 x x x 对于任意的 i = 1 , 2 , … , k i=1,2, \dots,k i=1,2,…,k 均满足 x ≡ a i ( m o d n i ) x ~\equiv~ a_i~(mod~n_i) x ≡ ai (mod ni)
当 i ≠ j i\neq j i=j 时,有
m j ≡ 0 ( m o d n i ) m_j \equiv 0~(mod~ n_i) mj≡0 (mod ni)
则对于
c j ≡ m j ≡ 0 ( m o d n i ) c_j \equiv m_j \equiv 0 ~(mod ~n_i) cj≡mj≡0 (mod ni)
又根据
c i = m i × m i − 1 ≡ 1 ( m o d n i ) c_i = m_i\times m_i^{-1}\equiv 1~(mod~n_i) ci=mi×mi−1≡1 (mod ni)
则对于 x x x 有
x ≡ ∑ j = 1 k a j c j ( m o d n i ) ≡ a i c i ( m o d n i ) ≡ a i × 1 ( m o d n i ) ≡ a i ( m o d n i ) x\equiv\displaystyle\sum_{j=1}^ka_j c_j ~~~~~~(mod ~n_i) \\ \equiv a_ic_i~~\qquad(mod n_i) \\ \equiv a_i\times1~~~~~~(mod n_i) \\ \equiv a_i~~~~~\qquad(mod n_i) x≡j=1∑kajcj (mod ni)≡aici (modni)≡ai×1 (modni)≡ai (modni)
得证
求模意义下的逆元
则本题的思路变得很清晰,现在问题来到如何求模意义下的逆元
我们来看一个式子
a a − 1 ≡ 1 ( m o d c ) aa^{-1} \equiv 1~(mod ~c) aa−1≡1 (mod c)
变形可得
a a − 1 = k c + 1 aa^{-1} = kc+1 aa−1=kc+1
移项
a a − 1 − k c = 1 aa^{-1} -kc =1 aa−1−kc=1
观察发现形如欧几里得方程
a x + b y = c ax+by=c ax+by=c
故可用扩展欧几里得求解
完整代码
import java.io.*;
import java.util.*;
class Main
{
static long sum=1;
static int n;
static int[] a=new int[10];
static int[] c=new int[10];
static long x;
static long y;
static long res=0;
public static long exgcd(long a,long b)
{
if(b==0)
{
x=1;
y=0;
return a;
}
long d=exgcd(b,a%b);
long tmp=x;
x=y;
y=tmp-(a/b)*x;
return d;
}
public static void main(String[] agrs)throws IOException
{
BufferedReader reader=new BufferedReader(new InputStreamReader(System.in));
n=Integer.parseInt(reader.readLine());
for(int i=0;i<n;i++)
{
String[] param=reader.readLine().split(" ");
c[i]=Integer.parseInt(param[0]);
a[i]=Integer.parseInt(param[1]);
sum*=c[i];
}
for(int i=0;i<n;i++)
{
long m=sum/c[i];
long re=exgcd(m,c[i]);
res=(res+a[i]*m*x%sum)%sum;
}
System.out.println((res%sum+sum)%sum);//输出正数
}
}
边栏推荐
- 【博主推荐】C#MVC列表实现增删改查导入导出曲线功能(附源码)
- Postman environment variable settings
- Windows下安装MongDB教程、Redis教程
- Install MySQL for Ubuntu 20.04
- Copy constructor template and copy assignment operator template
- API learning of OpenGL (2005) gl_ MAX_ TEXTURE_ UNITS GL_ MAX_ TEXTURE_ IMAGE_ UNITS_ ARB
- 解决:log4j:WARN Please initialize the log4j system properly.
- Mysql 其他主机无法连接本地数据库
- [ahoi2009]chess Chinese chess - combination number optimization shape pressure DP
- [BMZCTF-pwn] 12-csaw-ctf-2016-quals hungman
猜你喜欢

Why is MySQL still slow to query when indexing is used?
CSDN问答标签技能树(一) —— 基本框架的构建
机器学习--人口普查数据分析
CSDN question and answer module Title Recommendation task (I) -- Construction of basic framework
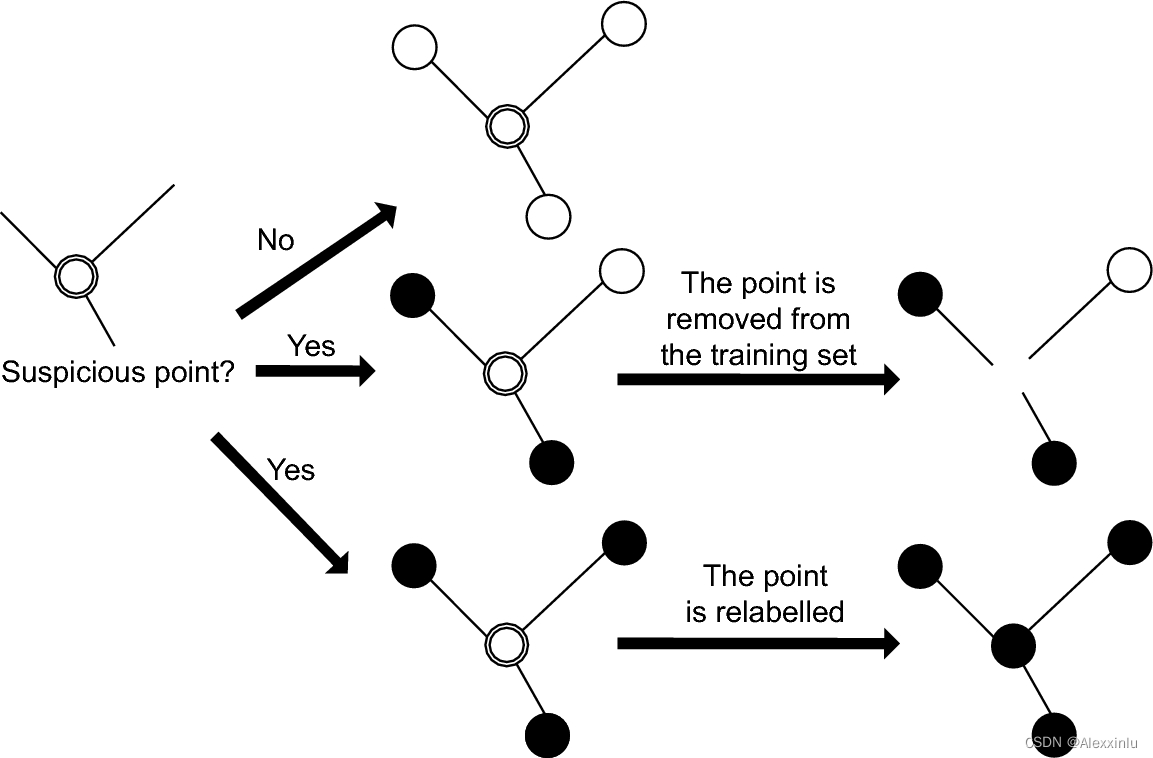
CSDN-NLP:基于技能树和弱监督学习的博文难度等级分类 (一)
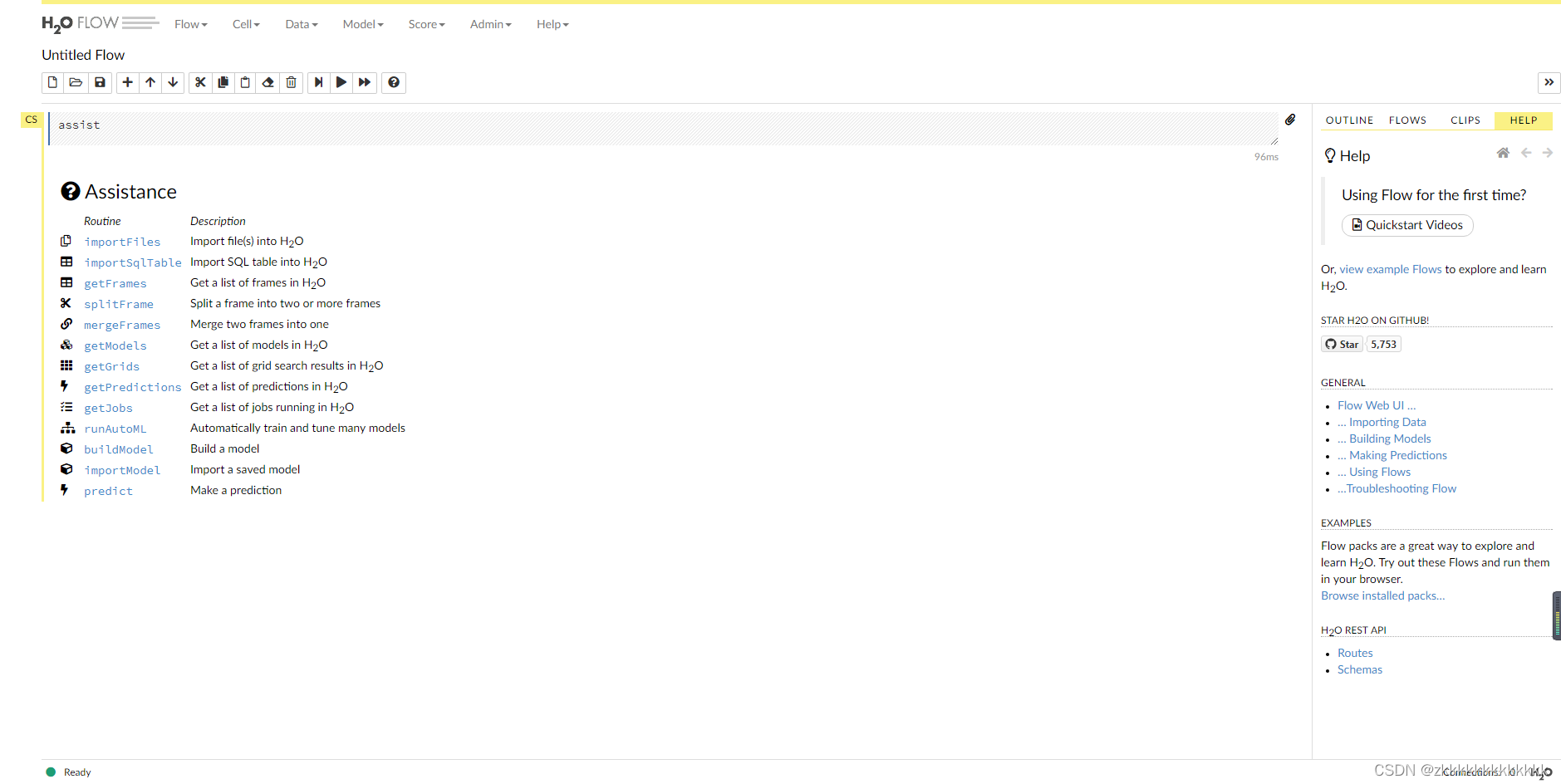
Introduction and use of automatic machine learning framework (flaml, H2O)
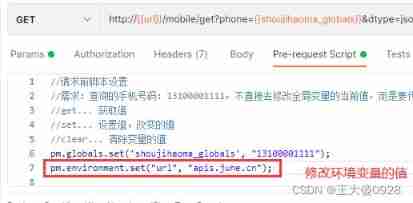
Postman uses scripts to modify the values of environment variables
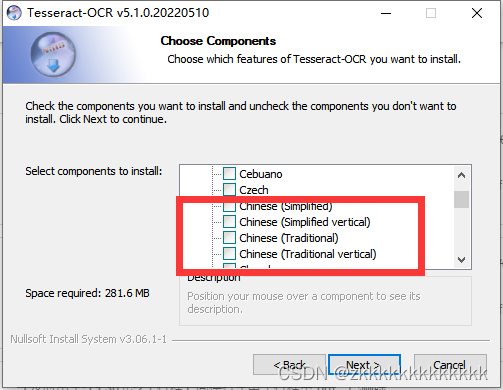
图像识别问题 — pytesseract.TesseractNotFoundError: tesseract is not installed or it‘s not in your path
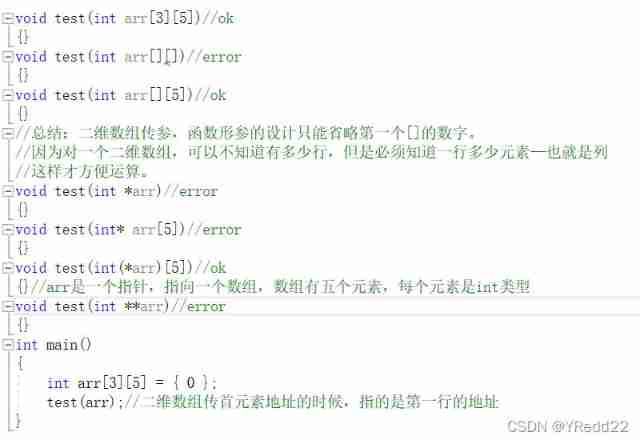
C language advanced pointer Full Version (array pointer, pointer array discrimination, function pointer)
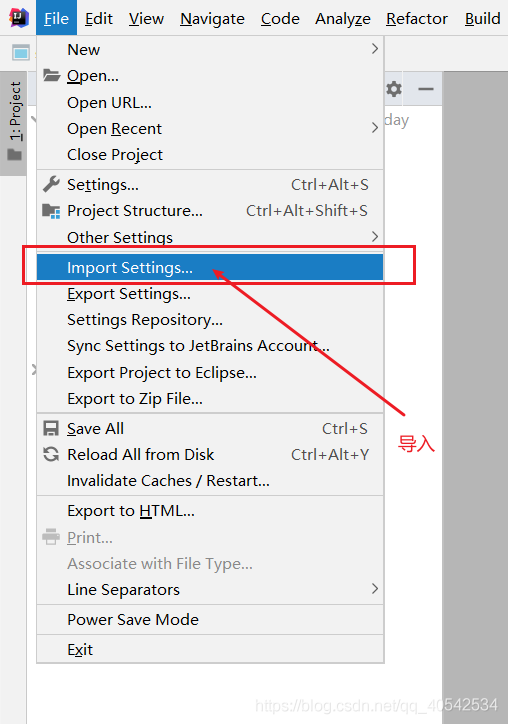
IDEA 导入导出 settings 设置文件
随机推荐
Mysql21 - gestion des utilisateurs et des droits
FRP intranet penetration
Deoldify项目问题——OMP:Error#15:Initializing libiomp5md.dll,but found libiomp5md.dll already initialized.
Why can't I use the @test annotation after introducing JUnit
Some notes of MySQL
JDBC原理
Attention apply personal understanding to images
[recommended by bloggers] C MVC list realizes the function of adding, deleting, modifying, checking, importing and exporting curves (with source code)
Windows下安装MongDB教程、Redis教程
MySQL主从复制、读写分离
MySQL 20 MySQL data directory
SSM整合笔记通俗易懂版
图片上色项目 —— Deoldify
QT creator specify editor settings
Mysql 其他主机无法连接本地数据库
Swagger、Yapi接口管理服务_SE
Invalid default value for 'create appears when importing SQL_ Time 'error reporting solution
数数字游戏
[Li Kou 387] the first unique character in the string
++Implementation of I and i++