当前位置:网站首页>POJ1821 Fence 题解报告
POJ1821 Fence 题解报告
2022-07-07 08:49:00 【Aurora_yxy】
1 题目描述
A team of $k (1 <= K <= 100) $workers should paint a fence which contains N ( 1 < = N < = 16000 ) N (1 <= N <= 16 000) N(1<=N<=16000) planks numbered from 1 1 1 to N N N from left to right. Each worker i ( 1 < = i < = K ) i (1 <= i <= K) i(1<=i<=K) should sit in front of the plank S i S_i Si and he may paint only a compact interval (this means that the planks from the interval should be consecutive). This interval should contain the Si plank. Also a worker should not paint more than Li planks and for each painted plank he should receive P i ( 1 < = P i < = 10000 ) P_i (1 <= P_i <= 10 000) Pi(1<=Pi<=10000). A plank should be painted by no more than one worker. All the numbers Si should be distinct.
Being the team’s leader you want to determine for each worker the interval that he should paint, knowing that the total income should be maximal. The total income represents the sum of the workers personal income.
Write a program that determines the total maximal income obtained by the K workers.
有 N N N 块木板从左至右排成一行,有 K K K 个工匠对这些木板进行粉刷,每块木板至多被粉刷一次。第 i i i 个工匠要么不粉刷,要么粉刷包含木板 i i i 的,长度不超过 L i L_i Li的连续一段木板,每粉刷一块木板可以得到$P_i $的报酬。
求如何安排能使工匠们获得的总报酬最多。
输入
The input contains:
Input
N K
L1 P1 S1
L2 P2 S2
…
LK PK SK
Semnification
N -the number of the planks; K ? the number of the workers
Li -the maximal number of planks that can be painted by worker i
Pi -the sum received by worker i for a painted plank
Si -the plank in front of which sits the worker i
输出
The output contains a single integer, the total maximal income.
样例
样例输入1
8 4
3 2 2
3 2 3
3 3 5
1 1 7
样例输出1
17
提示
Explanation of the sample:
the worker 1 paints the interval [1, 2];
the worker 2 paints the interval [3, 4];
the worker 3 paints the interval [5, 7];
the worker 4 does not paint any plank
2 思路
2.1 暴力无优化
先将所有工匠按照Si从小到大排序
• 状态:f[i][j],前 i 个工匠粉刷前 j 块木板(允许为空)的最大报酬。
• 状态转移方程:
第 i i i个工匠什么都不刷: f [ i ] [ j ] = f [ i − 1 ] [ j ] f[i][j]=f[i-1][j] f[i][j]=f[i−1][j]
第 j j j块木板可以空着不刷: f [ i ] [ j ] = f [ i ] [ j − 1 ] f[i][j]=f[i][j-1] f[i][j]=f[i][j−1]
考虑第$ i $个工匠粉刷第 k + 1 j k+1~j k+1 j块,
𝑓[𝑖][𝑗] =𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] + 𝑃𝑖 ∗ (𝑗 − 𝑘)},其中𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1,𝑗 ≥ 𝑆𝑖
枚举 i i i, j j j, k k k,时间复杂度为 O ( n 2 k ) O(n^2k) O(n2k)
因为我们可以看到数据并没有那么小: 1 < = K < = 100 1 <= K <= 100 1<=K<=100, 1 < = N < = 16000 1 <= N <= 16 000 1<=N<=16000
显然就不行
以呢,我们考虑用优先队列优化
2.2 优先队列优化dp
优化:𝑓[𝑖][𝑗] =𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] + 𝑃𝑖 ∗ (𝑗 − 𝑘)},其中𝑗 ≥ 𝑆𝑖,𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1
• 将最外层循环i看作定值,考虑内层循环 j 和决策 k ,转换得到:
• 𝑓[𝑖][𝑗] = 𝑃𝑖 ∗ 𝑗 +𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] − 𝑃𝑖 ∗ 𝑘)},其中𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1,𝑗 ≥ 𝑆𝑖
维护一个决策点k单调递增,数值 f [ i − 1 ] [ k ] − P i × k f[i-1][k]-Pi×k f[i−1][k]−Pi×k单调递减的队列,
只有这个队列中的决策才有可能成为某一刻的最优决策
• 单调队列支持:
当 j 变大时,检查队头,将小于j-Li的出队。
查询最优决策时,队头为所求最大值
新决策入队时,检查队尾 f [ i − 1 ] [ k ] − P i × k f[i-1][k]-Pi×k f[i−1][k]−Pi×k的单调性,无用决策出队,新
决策入队
2 具体实现
- 对于每一个外层循环i,
当内层循环开始时( j = S i j=S_i j=Si),建立一个空的单调队列,
将区间 [ m a x ( j − L i , 0 ) , S i − 1 ] [max(j-Li,0),Si-1] [max(j−Li,0),Si−1]的决策加入到单调队列中,执行3
- 对于每一个 j = S i N j=Si~N j=Si N,
先检查队头是否合法(1),再取队头为最优策略(操作2)进行状态转移,再进行入队(3)
总时间复杂度为O(NK)
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+2,K=1e2+2;
struct node{
int l,s,p;
}a[K];
bool cmp(node x,node y){
return x.s<y.s;
}
int f[K][N],q[N],n,k;
int main(){
while(~scanf("%d%d",&n,&k)){
for(int i=1;i<=k;i++) {
scanf("%d%d%d",&a[i].l,&a[i].p,&a[i].s);
}
sort(a+1,a+k+1,cmp);
memset(f,0,sizeof(f));
for(int i=1;i<=k;i++){
int hd=0,tl=0;
q[tl++]=max(0,a[i].s-a[i].l);
for(int j=1;j<=n;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(j>=a[i].s+a[i].l) continue;
while(hd<tl&&q[hd]+a[i].l<j) hd++;
if(j>=a[i].s) f[i][j]=max(f[i][j],f[i-1][q[hd]]+a[i].p*(j-q[hd]));
else{
int x=f[i-1][j]-j*a[i].p;
while(hd<tl&&f[i-1][q[tl-1]]-q[tl-1]*a[i].p<x) tl--;
q[tl++]=j;
}
}
}
printf("%d\n",f[k][n]);
}
return 0;
}
完结撒花*
·*,°*:.*( ̄▽ ̄)/$:.°* 。
边栏推荐
- 【推荐系统 02】DeepFM、YoutubeDNN、DSSM、MMOE
- What is an intermediate network engineer? What is the main test and what is the use?
- CSAPP bomb lab parsing
- BUUCTF---Reverse---reverse1
- [système recommandé 01] rechub
- VR development optimization
- Long list performance optimization scheme memo
- 555 circuit details
- 單調性約束與反單調性約束的區別 monotonicity and anti-monotonicity constraint
- Unity script visualization about layout code
猜你喜欢
![[machine learning 03] Lagrange multiplier method](/img/14/7d4eb5679606e272f137ddbda4938c.png)
[machine learning 03] Lagrange multiplier method

【亲测可行】error while loading shared libraries的解决方案
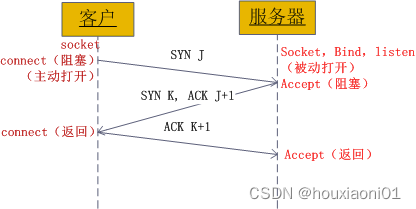
Socket communication principle and Practice
高级软考(网络规划设计师)该如何备考?
Is the soft test intermediate useful??
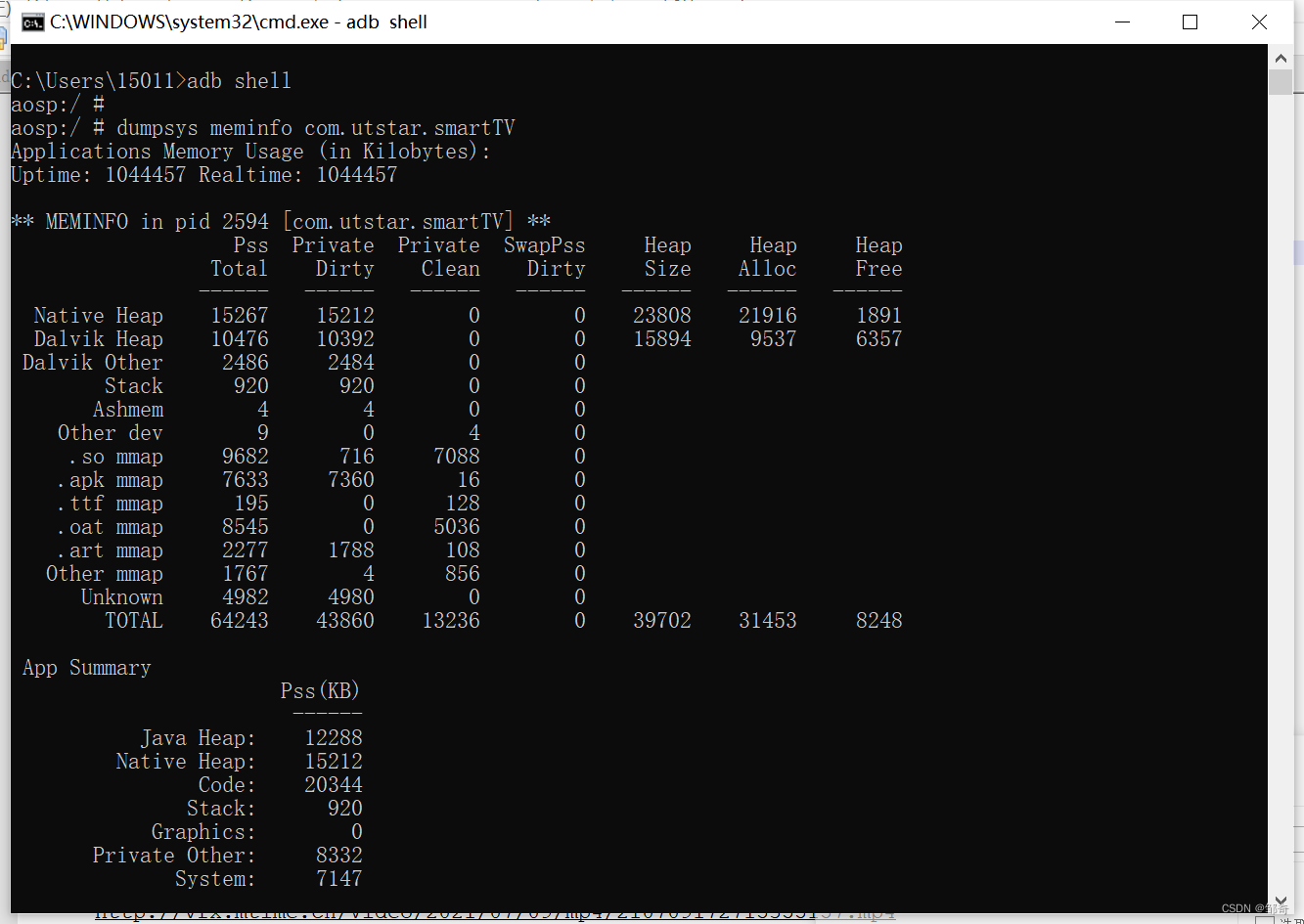
ADB utility commands (network package, log, tuning related)
What are the test preparation materials and methods for soft exam information processing technicians?
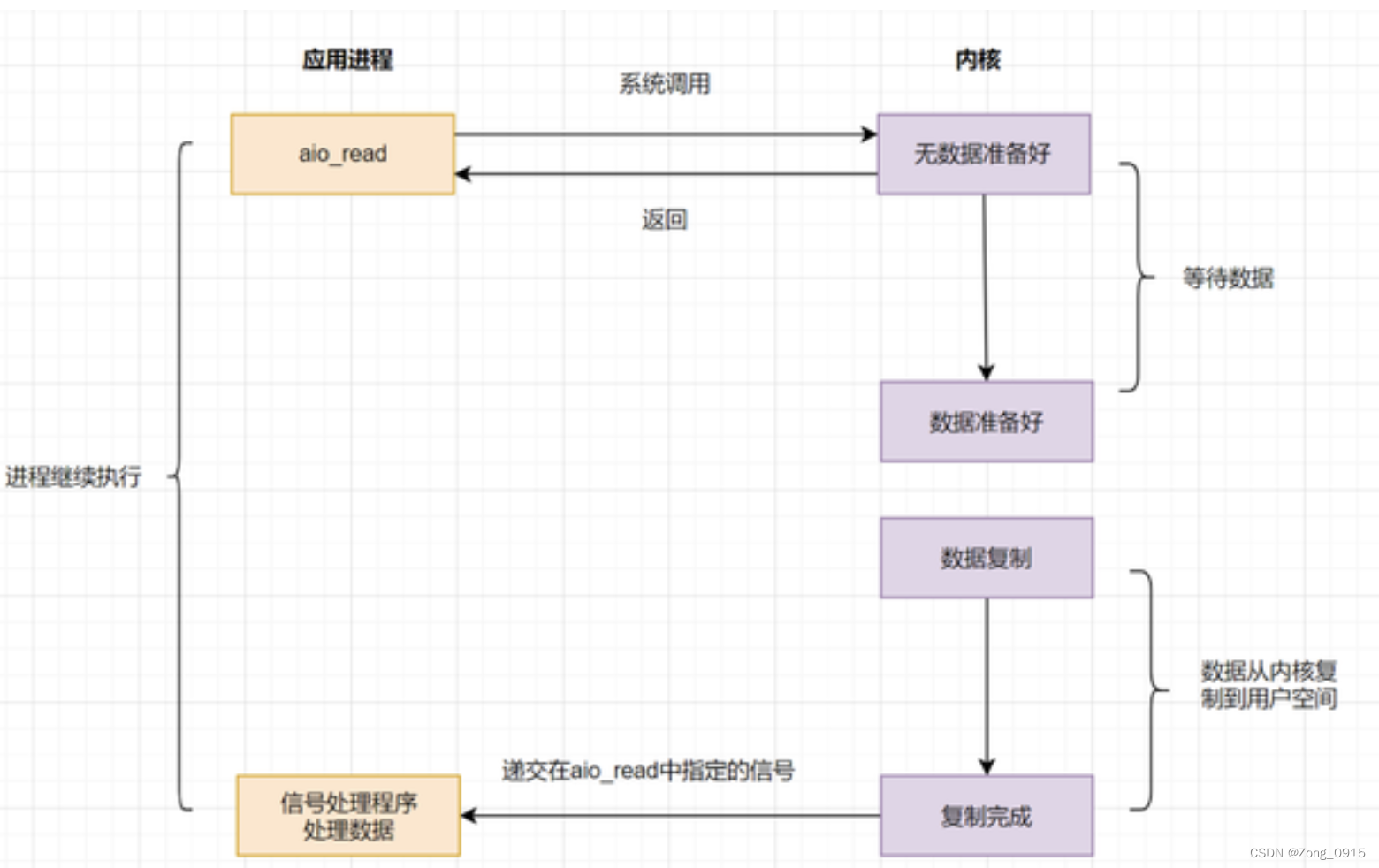
IO model review

优雅的 Controller 层代码
![[installation system] U disk installation system tutorial, using UltraISO to make U disk startup disk](/img/41/3a9450a84291ba04caee65241bce5d.png)
[installation system] U disk installation system tutorial, using UltraISO to make U disk startup disk
随机推荐
[actual combat] transformer architecture of the major medical segmentation challenges on the list --nnformer
Five simple and practical daily development functions of chrome are explained in detail. Unlock quickly to improve your efficiency!
[système recommandé 01] rechub
Mendeley--免费的文献管理工具,给论文自动插入参考文献
2022.7.3DAY595
Schnuka: working principle of robot visual grasping machine visual grasping
MONAI版本更新到 0.9 啦,看看有什么新功能
关于easyflash v3.3使用过程的记录
Différences entre les contraintes monotones et anti - monotones
软考一般什么时候出成绩呢?在线蹬?
Realize ray detection, drag the mouse to move the object and use the pulley to scale the object
单调性约束与反单调性约束的区别 monotonicity and anti-monotonicity constraint
1324: [example 6.6] integer interval
ArrayList线程不安全和解决方案
Simple and easy to modify spring frame components
简单易修改的弹框组件
How to successfully pass the senior system architecture designer in the second half of the year?
MySQL insert data create trigger fill UUID field value
【亲测可行】error while loading shared libraries的解决方案
July 10, 2022 "five heart public welfare" activity notice + registration entry (two-dimensional code)