当前位置:网站首页>Method recursion (Fibonacci sequence, frog jumping steps, tower of Hanoi problem)
Method recursion (Fibonacci sequence, frog jumping steps, tower of Hanoi problem)
2022-07-02 08:22:00 【Ischanged】
The concept of recursion
What is recursion ?
The programming skill of program calling itself is called recursion ( recursion). Recursion as an algorithm is widely used in programming languages . A procedure or function has a method that directly or indirectly calls itself in its definition or description , It usually transforms a large and complex problem into a smaller problem similar to the original problem to solve , The recursion strategy only needs a few programs to describe the repeated calculation needed in the process of solving problems , Greatly reduces the amount of code in the program . The main way to think about recursion is : Turn the big thing into a small one
Two necessary conditions for recursion :
- There are restrictions , When this constraint is met , Recursion doesn't continue .
- After each recursive call, it gets closer and closer to this constraint .
Detailed analysis of recursive execution process
Code example : Recursive search N The factorial :
public static void main(String[] args) {
int n = 3;
int ret = factor(n);
System.out.println("ret = " + ret);
}
public static int factor(int n) {
if (n == 1) {
return 1;
}
return n * factor(n - 1); // factor Call the function itself
}
** Suppose we ask 3 Factorial of , requirement 3 The factorial , Can be converted to 3 ride 2 The factorial , You can ask first 2 The factorial , requirement 2 The factorial of can be found first 1 The factorial , cube 2,1 After the factorial of , Recursion condition is not satisfied , Just return the value step by step to the internal quadrature of the calling function , In this way, if it is a complex problem, it can be simplified into a very simple problem ,** Simplify some repetitive steps ; For example, requirements n The factorial , Just ask for (n-1) The factorial , Then multiply by n, requirement (n-1) The factorial , Just ask for (n-2) The factorial of is multiplying (n-1) that will do , Always find 1 Until the factorial of . Here, you may not realize the simplicity of recursion in the simple problem of factorial , But let's first understand recursion from a simple problem , Looking at difficult problems .
Diagram analysis code execution process :

Above is beg 3 Code execution flow of factorial of , Actually, recursion , Namely “ Deliver ” Go on to the small side of the problem ,“ return ” Return to , When the program reaches a certain condition , Return to the starting delivery position .
The general process is as follows :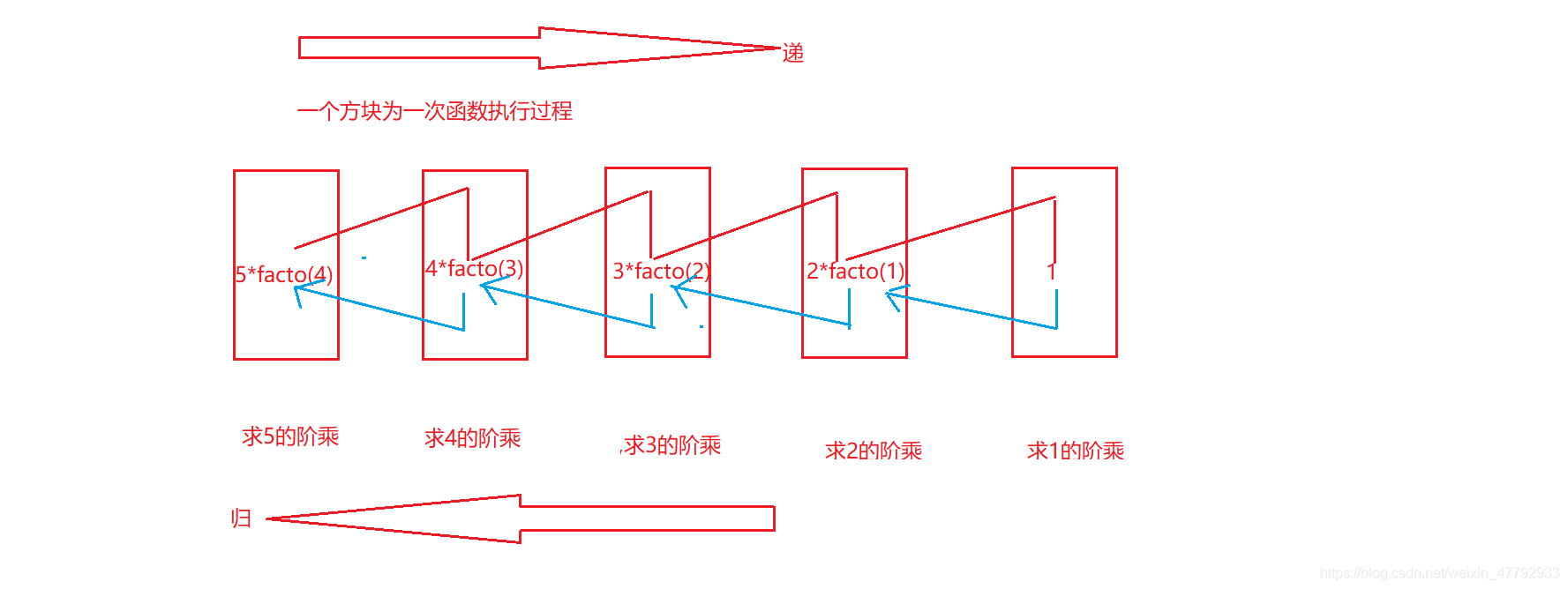
When a function is called , Function opens up space on the stack , The parameters of the function , local variable , Return the data , The return address is also opened on the stack , Stack features first in and last out , Understanding this can help us understand the recursive function “ return ” The process of , You can taste it carefully .
Analysis and solution of classical recursive problems
Recursion itself is a little abstract and a little hard to think of , Find more rules and draw pictures to understand , The key of recursion is to find recursion formula , If you can find a recursive formula, it is very simple to write lines of code according to the formula . For some problems such as recursion and non recursion, it is better not to use recursion , Non recursive is more efficient .
Fibonacci series question
Fibonacci sequence (Fibonacci sequence), Also called golden section series , Leonardo the mathematician · Fibonacci (Leonardoda Fibonacci) Take rabbit breeding as an example , It is also called “ Rabbit Series ”, It refers to such a sequence :0、1、1、2、3、5、8、13、21、34、…… In Mathematics , The Fibonacci sequence is defined recursively as follows :F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
Code implementation Fibonacci sequence
public static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
return fib(n - 1) + fib(n - 2);
}
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int a=scanner.nextInt();
System.out.println(fib(a));
}
It is easy to see from the form of Fibonacci sequence , Its law , Get its recurrence formula , Start with the third Fibonacci number , Fibonacci numbers are the sum of the first two numbers , The first two numbers are 1. Suppose the hundredth Fibonacci number sequence is required , Ask for the ground first 99 And the 98 individual , Requirement No 99 Another request 98,97 individual …, And so on , It can be seen that Fibonacci sequence also follows the principle of making things smaller , It is also a recursive problem , Of course, it is simple to find Fibonacci sequence by recursion , But in the evaluation process, many repeated calculations are made, and the efficiency is too low ,( Draw a tree diagram, simply look at the second understand ) The non recursive method can also be used to find the sequence , Cycles are more efficient .
Non recursive Fibonacci sequence :
public static int fib(int n) {
int a=1;
int b=1;
int c=1;
while (n>2) {
c=a+b;
a=b;
b=c;
n--;
}
return c;
}
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int n= scanner.nextInt();
System.out.println(fib(n));
}
The problem of frog jumping on the steps
Topic linking
A frog can jump up at a time 1 Stepped steps , You can jump on it 2 level . Ask the frog to jump on one n How many jumps are there in the steps ?
For a question , The first thing we get is to think , This calculation calculates , This drawing draws , Find the rules , Write code after the key points .
Situation 1 , There is only one step , Jumping one step at a time only 1 Jump

Situation two , There are two steps , You can jump step by step , You can also jump two steps at a time , There are two ways to jump

Situation three , There are three steps , Because the title says , The little frog can only jump one or two steps at a time **, So there are two scenarios , If you jump a step , Then there are two steps behind , Jumping method is similar to situation two ; If the frog jumps two steps , Then there is only one step behind , This is the same as the jump method of situation one **. In this way, we probably understand , Case 3 has three steps , Two cases , The total jumping method is the sum of the first two step jumping methods 3 Kind of .

Then let's think about it roughly, if there is 4 Where are the steps , More steps ?
The little frog jumps one or two steps at a time , If you jump one step, there are three steps behind it , Isn't the later jumping method the same as the jumping method of three steps ? If you jump two steps , The remaining two steps , The jumping method is the same as that of two steps . In this way, we can get , If there is n Steps , The jumping method of the little frog is ,(n-1 rank ) Jump method , add (n-2) Step jump . In this way, we find that this problem is also a recursive problem , requirement n The jumping method of order is too complicated , We decompose it into small problems and evaluate it upside down , Ask this n Order problem , It is decomposed into a solution based on first-order and second-order . The inductive formula of frog jumping steps is F(1)=1,F(2)=2, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*), We can see that the frog jumping the steps is evolved from the Fibonacci sequence .
Code implementation :
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int n = scanner.nextInt(); // Number of steps
System.out.println(jumpFloor(n));
}
public static int jumpFloor(int floor) {
if (floor == 1) {
// Situation 1
return 1;
}
if (floor == 2) {
// Situation two
return 2;
}
return jumpFloor(floor - 1) + jumpFloor(floor - 2); // Function recursion
}
Mutant frog jumps steps
Title Description
Topic linking
A frog can jump up at a time 1 Stepped steps , You can jump on it 2 level …… It can also jump on n level . Ask the frog to jump on one n Steps of steps (n As a positive integer ) How many jumps are there in total .
analysis :
The number of steps that the mutant frog jumps on the steps is not specified , So frogs jump more and more , For example, one step jump , Any step , Jump directly from the ground to the highest level , Brave frogs can jump , And all the previous jumps , Now frogs can jump out , Suppose the jumping method of jumping directly from the ground is f(0)=1, We derive the recursive formula from the graph , Then if there is n The jumping method of steps is f(n) = f(n-1) + f(n-2) +....+f(0),(f(0),f(1) All for 1). The time complexity of recursion :O(N^N), Spatial complexity :O(N).
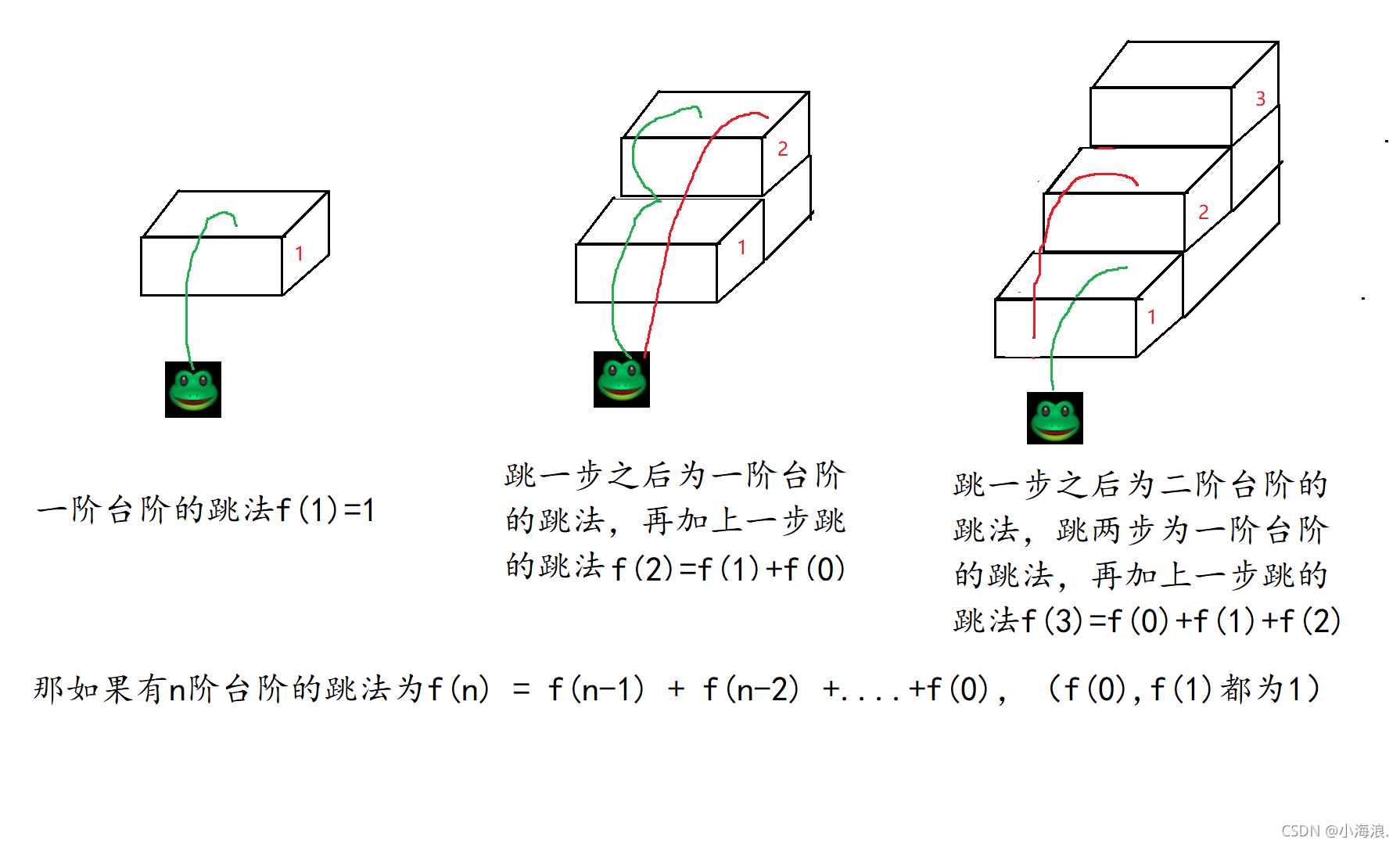
Then the recursive code is as follows :
public class Test {
public static int jumpFloorII(int number) {
int sum = 1;
for(int i = 1; i<number;i++)
sum += jumpFloorII(number-i); // Calculation f(number-1)
return sum;
}
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int a=scanner.nextInt();
System.out.println(jumpFloorII(a));
}
The same idea as recursion , But ordinary recursion does many useless calculations . For example, in the above recursion ,f(1),f(2)… Calculated multiple times . We can optimize , There are many ways , I chose the best understood simple , Mathematical way to solve ,f[n] = f[n-1] + f[n-2] + … + f[0], that f[n-1] = f[n-2] + f[n-3] + … + f[0]
So a merger ,f[n] = 2*f[n-1],f[n]/f[n-1]=2 Initial conditions f[0] = f[1] = 1, Is an equal ratio sequence , After that, the general term formula of the proportional series is f[n]=2^(n-1), Time complexity :O(n), Spatial complexity :O(1)
Code implementation :
public class Test {
public static int jumpFloorII(int number) {
if(number==1||number==0) return 1;
return 1<<number-1; // formula : Left shift multiplication 2, Right remove 2
}
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int a=scanner.nextInt();
System.out.println(jumpFloorII(a));
}
}
The hanotta problem
Topic linking
The tower of Hanoi problem is a classic one . Hanoi (Hanoi Tower), Also known as the river tower , From an old Indian legend . Vatican made three diamond pillars when he created the world , Stack on a column from bottom to top in order of size 64 A golden disk . Brahman ordered Brahman to rearrange the disc from below on another pillar in order of size . And stipulate , anytime , You can't put it on a small disc on a large disc , Take and place the disc on the column , Don't put the disc in another position , And you can only move one disc at a time between the three pillars . Ask how to operate ?
The three pillars are named A,B,C, Take any disc from the first column A Move up to the last column C The basic idea of :
1. When n=1 When , Direct the disc from A The disk moves to C disc
When n>1 When
1. take A On the column n-1 With the help of C The column moves to B On the column
2. take A On the column n Plates move to C Above the column .
3. take B On the column n-1 The plates move to C Above the column
Simple analysis :
First, recursion goes deep with the level of recursion , The problem is getting more and more complicated , Very abstract , Reaching a certain scale is beyond the human brain , We can only find the law through simple recursion , Then write the code . The situation of two plates and three plates is very simple and easy to imagine , Suppose there are three plates , Let's first put the 2 A plate passed C Move to B( When there are multiple plates, be sure to move with the help of other plates , Only in this way can we ensure that the big plate is under ),** Then move the third plate to C column , hold A above 2 The plates move to B There is another recursive operation on the column. Is it a problem with the original problem ? It's just that there are fewer plates , The actual parameters passed recursively each time also change ,** The actual parameters passed are brought in every recursion . So if you move n Is the idea of a plate the same as that mentioned above , Does this reflect the idea of recursion ,“ Make a big deal small ”, Each recursion is closer to the condition of the end of recursion , Learn recursion slowly , First, from simple to complex , Understand the process from simple to complex , Complex process need not be too tight , That's how to implement the idea like a simple one , If you really go to every step , I think it's hard to understand recursion .
A plate A->C,1=2^1-1
Two plates : A->B A->C B->C , Move three times , 3= 2^2 -1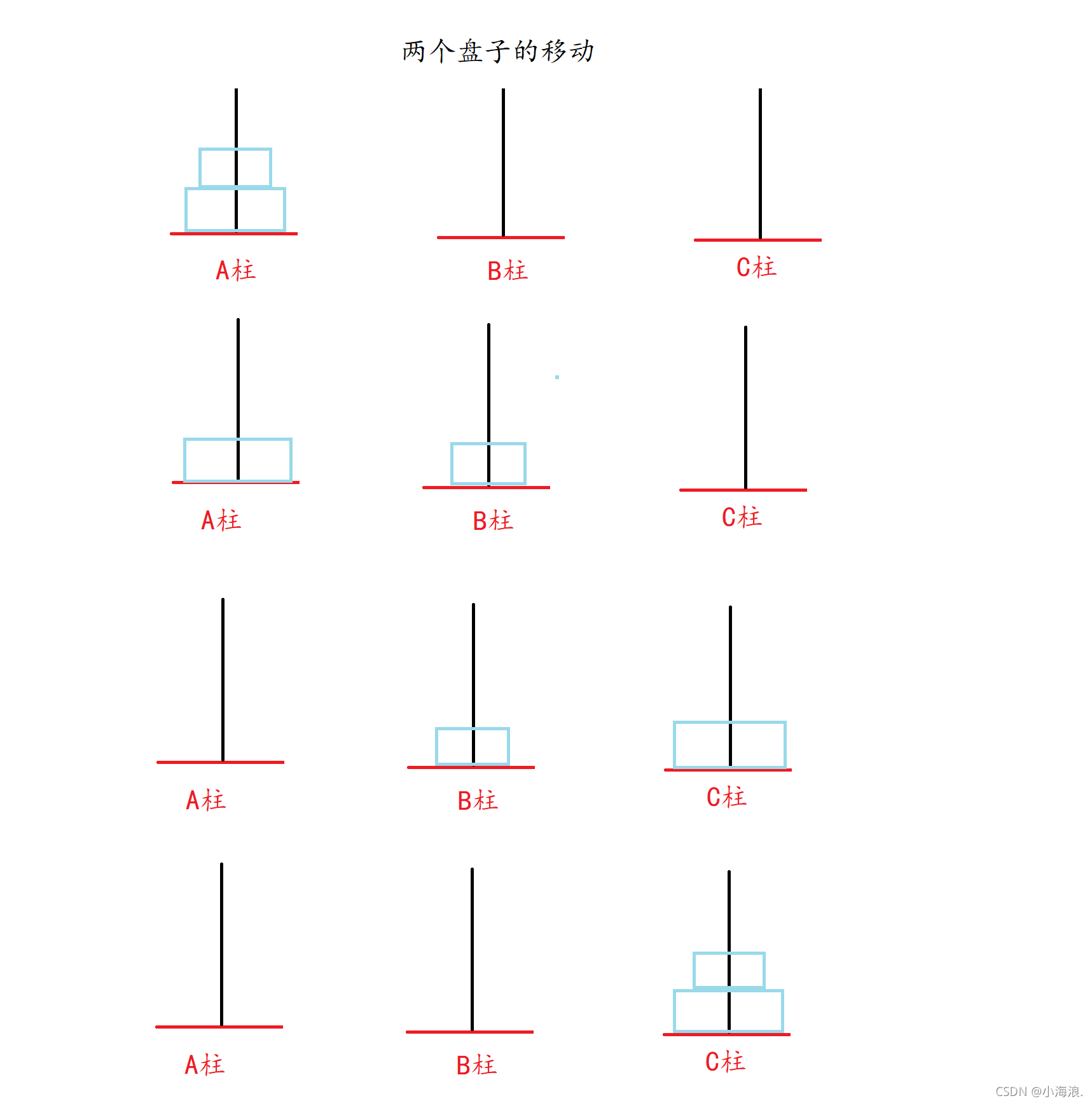
The movement of three plates :
A->C A->B C->B A->C B->A B->C A->C , 7 =2^3 -1
There are three plates , Let's first put the 2 A plate passed C Move to B The blue one is a recursion , Use the first recursive function , Then move the third plate to C Behind the column , hold A above 2 The plates move to B Above the column is another lump, another recursion .
The number of movements of one, two, three plates from the top , We can conclude that , Move n The number of plates is 2^n-1 Time ,, Back to the original question , When there is 64 A golden disc , If the number of times to move is 2 ^ 64-1, If you move once a second , You need to 2 ^64-1=1.845*10 ^19, about 5849 In one hundred million, ! You can imagine how complicated the problem is .
Code example :
public class TestDemo {
public static void move(char pos1,char pos2) {
System.out.print(pos1+"->"+pos2+" ");
}
/** * * @param n Current number of plates * @param pos1 The starting position * @param pos2 Transfer location * @param pos3 Destination location */
public static void hanoiTower(int n,char pos1,char pos2,char pos3) {
// The arguments passed in will change
if(n == 1) {
move(pos1,pos3);
}else {
hanoiTower(n-1,pos1,pos3,pos2);
move(pos1,pos3);
hanoiTower(n-1,pos2,pos1,pos3);
}
}
public static void main(String[] args) {
hanoiTower(1,'A','B','C');
System.out.println();
hanoiTower(2,'A','B','C');
System.out.println();
hanoiTower(3,'A','B','C');
System.out.println();
}
}
️ Too small 🧑*🧑* If 9️⃣ Remember to hold in words ,
边栏推荐
- My VIM profile
- STL速查手册
- Comparison between setTimeout and requestanimationframe (page refresh)
- Global and Chinese market of tillage finishing machines 2022-2028: Research Report on technology, participants, trends, market size and share
- Sqlyog remote connection to MySQL database under centos7 system
- One of the reasons for WCF update service reference error
- STM32-新建工程(参考正点原子)
- On the confrontation samples and their generation methods in deep learning
- 多站点高可用部署
- In depth understanding of prototype drawings
猜你喜欢

Static library and dynamic library

Development of digital collection trading website development of metauniverse digital collection
旋转链表(图解说明)
The internal network of the server can be accessed, but the external network cannot be accessed

静态库和动态库
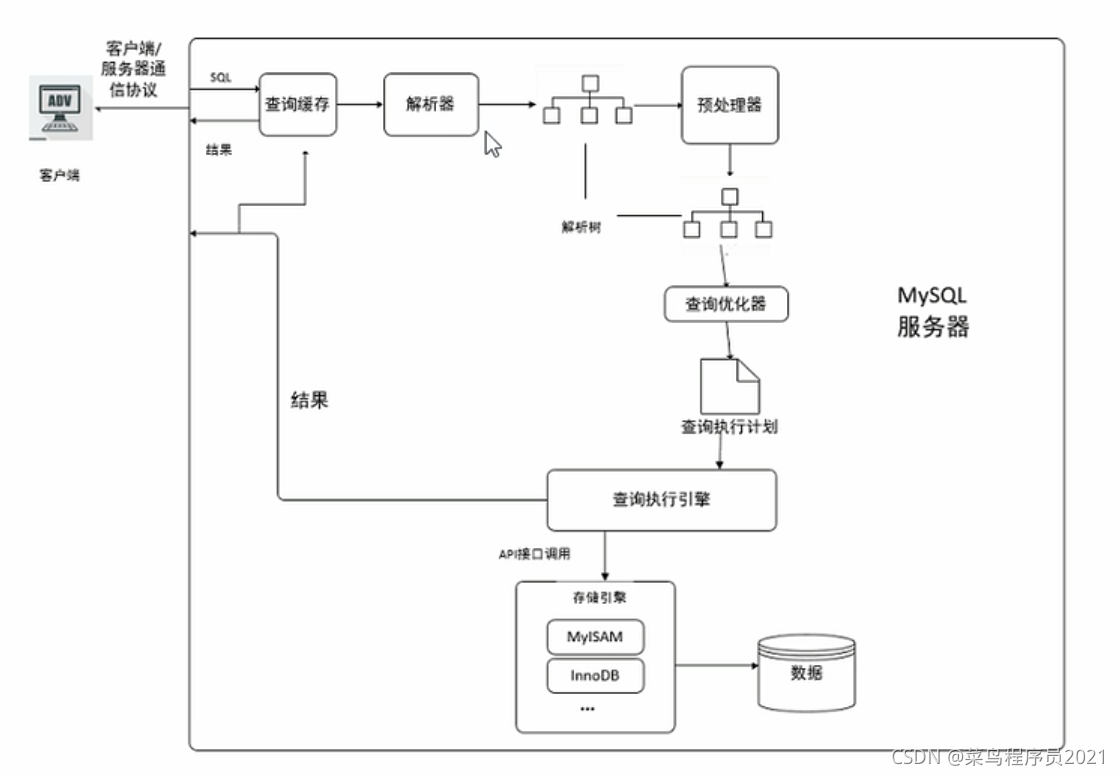
MySQL优化
C语言实现XML生成解析库(XML扩展)
STM32-新建工程(参考正点原子)
Sqlyog remote connection to MySQL database under centos7 system
Installation and use of simple packaging tools
随机推荐
Installation and use of simple packaging tools
E-R draw clear content
Comparable,Comparator,Clonable 接口使用剖析
Meta learning Brief
Animation synchronization of CarSim real-time simulation
Global and Chinese market of electric cheese grinder 2022-2028: Research Report on technology, participants, trends, market size and share
Sqlyog remote connection to MySQL database under centos7 system
力扣方法总结:滑动窗口
最长等比子序列
Short video with goods source code, double-click to zoom in when watching the video
w10升级至W11系统,黑屏但鼠标与桌面快捷方式能用,如何解决
AR system summary harvest
Generate database documents with one click, which can be called swagger in the database industry
Deep understanding of JVM
Opencv3 6.3 reduced pixel sampling with filters
VS Code配置问题
Several methods of image enhancement and matlab code
Global and Chinese market of wire loop, 2022-2028: Research Report on technology, participants, trends, market size and share
My VIM profile
程序猿学英语-指令式编程