Leetcode-15: sum of three numbers

Answer key ：

　　 You can also use Double pointer Algorithm , But there are three numbers ?

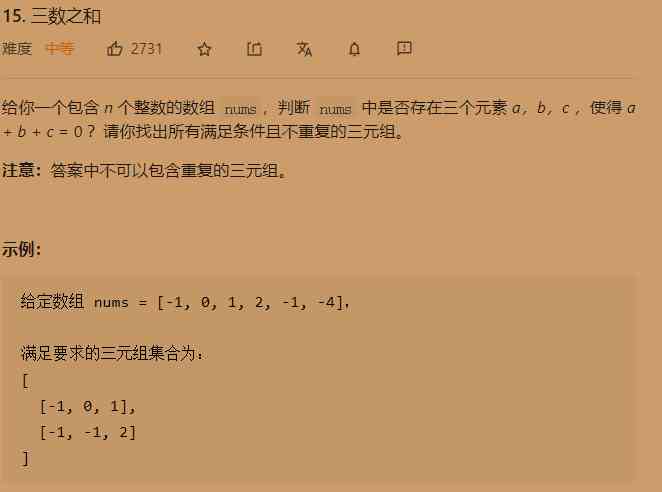
        This is the core point of this question , Let's enumerate the first point , The other two points use the double pointer algorithm , Sort first , Then go heavy. , For enumerating the first point , If there is a repetition, just take the first time , The following repeating elements can be directly pass fall .

        For the other two points , If there is repetition , It can be done in the same way as the first point , The same element directly pass fall .

        Using the double pointer algorithm can effectively reduce one $O(n)$ Time complexity of , The time complexity of the problem is $O(n^2)$.

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        //  A triple 
        vector <vector<int>> a;
        int target;
        sort(nums.begin(), nums.end());
        //  Let's set a point first target, And then scan it with two pointers 
        for (int i = 0; i < nums.size(); ++i) {
            //  Deduplication 
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            if ((target = nums[i]) > 0) {
                break;
            }
            //  Double pointer scans the other two points 
            int l = i + 1, r = nums.size() - 1;
            while (l < r) {
                if (target + nums[l] + nums[r] < 0) ++l;
                else if (target + nums[l] + nums[r] > 0) --r;
                else {
                    a.push_back({target, nums[l], nums[r]});
                    ++l;
                    --r;
                    //  Deduplication 
                    while (l < r && nums[l - 1] == nums[l]) ++l;
                    while (l < r && nums[r + 1] == nums[r]) --r;
                }
            }
        }
        return a;
    }
};

        The sum of four numbers is the same , Just one more cycle , I won't show you .