当前位置:网站首页>C - Divisors of the Divisors of An Integer Gym - 102040C
C - Divisors of the Divisors of An Integer Gym - 102040C
2022-07-05 14:01:00 【beyond+myself】
Topic link
The question : Is o n! The number of factors in the factor
Answer key :
①:n! The number of a factor in is n/x Accumulation .
prove : In fact, it is one layer at a time , That is, each removal can be divided into 1 individual 3 Of , Two in turn 3 Of , Three 3 The number of , Finally, you can get 3 The number of , There's no need to
to be divisible by , Because it's a factorial , So even if it can't be divisible , It can also be divided by smaller numbers in the array .
Let's give you an example :
1234567 We find what we finally get 2 The number of , for the first time We found that 2 4 6 Divisibility , After division, it becomes 1 2 3 then 7/2=3,ans+=3, then 2 Still divisible , And then it became 1, then 3/2=1, You can't divide the rest , So we can find this rule .
②: Suppose we can turn the result of factorial into something similar to 2 ^ a * 3 ^ b * 5 ^ c In this way , We can get the result —— yes (a+1)*(a+2) / 2 * (b+1) * (b+2) / 2 *(c+1) * (c+2) / 2;
prove : After we write them in the above form , In fact, the factor is easy to find , If you let me find the number of factors , That's all for this question , But the question requires the number of factors , So we can't finish here , The number of factors is —— We just ask
A prime unit , For example :3 ^ 0 The number of factors of is 1 individual ,3 ^ 1 Are the two ,3 ^ a The number of factors ( 3 ^ 0 ~ 3 ^ a) common a+1 individual therefore We add them up to (a+1) * (a+2)/2 such Multiply all of them , That is, the number of cases similar to permutation and combination , When all numbers are selected 0 Inferior time , That is to say 1.
Here is AC Code :
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int N=1e6+10,mod=1e7+7;
int prime[N];
bool st[N];
int cnt[N];
int cou;
void is_prime(int n)
{
int i,j;
for(i=2;i<=n;i++)
{
if(!st[i])
{
prime[cou++]=i;
for(j=i+i;j<=n;j+=i) st[j]=true;
}
}
}
signed main()
{
is_prime(1e6);
int n;
while(cin>>n&&n)
{
memset(cnt,0,sizeof(cnt));
for(int i=0;prime[i]<=n;i++)
{
cnt[i]=0;
int tmp=n;
while(tmp)
{
cnt[i]+=tmp/prime[i];
tmp/=prime[i];
}
}
int ans=1;
for(int i=0;prime[i]<=n;i++)
{
if(cnt[i]>0)
{
ans=(ans%mod*((cnt[i]+1)*(cnt[i]+2)/2)%mod)%mod;
}
}
printf("%lld\n",ans);
}
return 0;
}
边栏推荐
- Wechat app payment callback processing method PHP logging method, notes. 2020/5/26
- PHP basic syntax
- [buuctf.reverse] 152-154
- ZABBIX monitoring
- What is the future development trend of neural network Internet of things
- 嵌入式软件架构设计-消息交互
- Simple PHP paging implementation
- LeetCode_67(二进制求和)
- Anchor navigation demo
- Jetpack compose introduction to mastery
猜你喜欢

Laravel dompdf exports PDF, and the problem of Chinese garbled code is solved
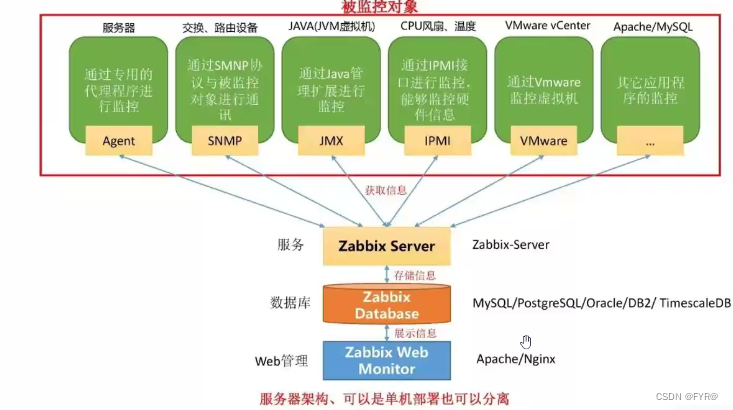
ZABBIX monitoring

让秒杀狂欢更从容:大促背后的数据库(下篇)
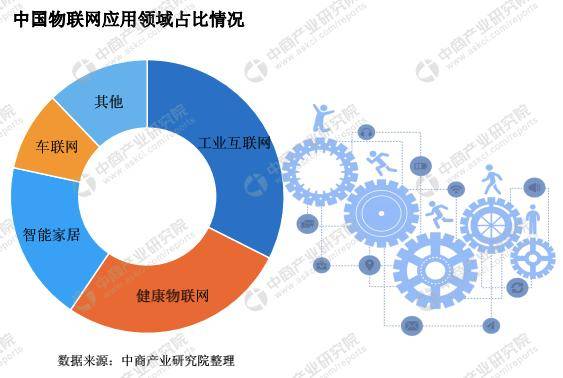
What is the future development trend of neural network Internet of things
![[South China University of technology] information sharing of postgraduate entrance examination and re examination](/img/a8/41e62a7a8d0a2e901e06c751c30291.jpg)
[South China University of technology] information sharing of postgraduate entrance examination and re examination
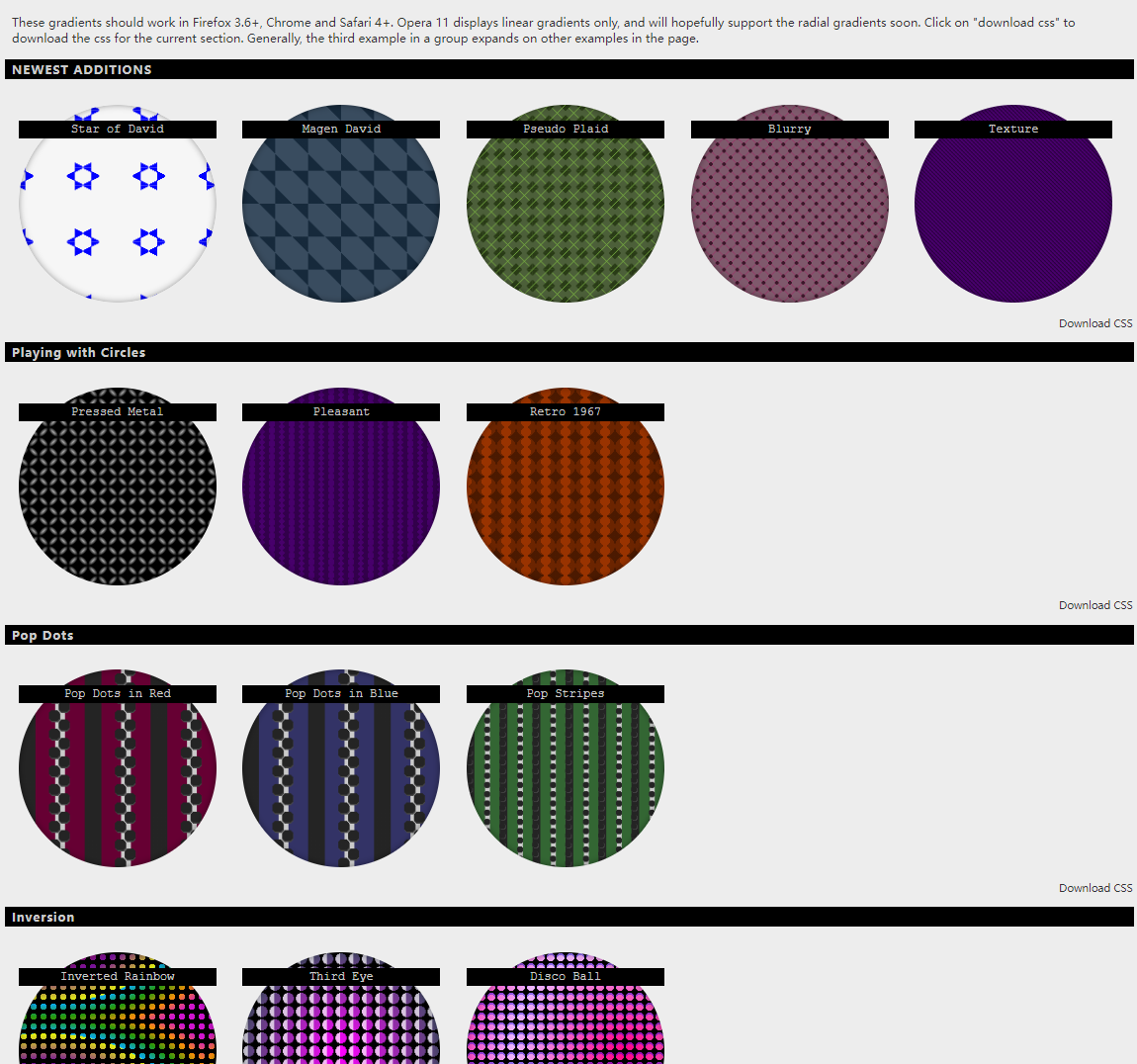
These 18 websites can make your page background cool
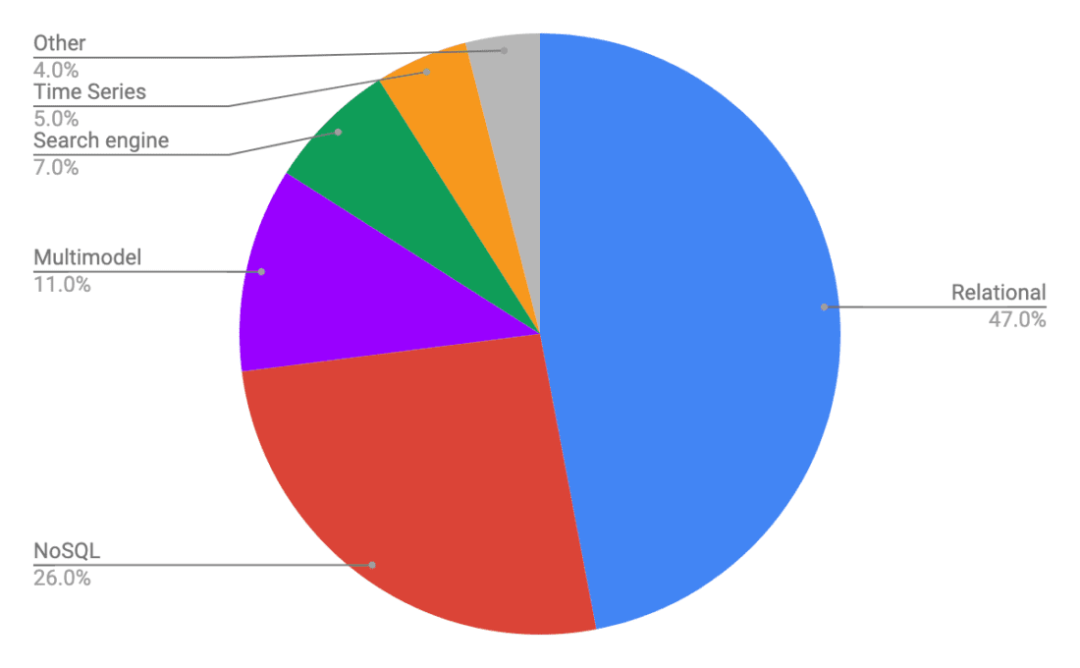
Comparison of several distributed databases
如何将 DevSecOps 引入企业?
治臻新能源冲刺科创板:年营收2.2亿 上汽创投是股东

研究生可以不用学英语?只要考研英语或六级分数高!
随机推荐
Elk enterprise log analysis system
POI set the data format of the column (valid)
Some ideas about Apache mesos
瑞能实业IPO被终止:年营收4.47亿 曾拟募资3.76亿
如何把大的‘tar‘存档文件分割成特定大小的多个文件
Self built shooting range 2022
研究生可以不用学英语?只要考研英语或六级分数高!
SAS接口有什么优势特点
-Web direction attack and defense world
web3.eth. Filter related
2022年机修钳工(高级)考试题模拟考试题库模拟考试平台操作
Request + BS4 crawl Netease cloud music popular comments
【华南理工大学】考研初试复试资料分享
PHP character capture notes 2020-09-14
关于Apache Mesos的一些想法
PHP generate Poster
Liste des liens (simple)
01 、Solr7.3.1 在Win10平台下使用jetty的部署及配置
[machine learning notes] several methods of splitting data into training sets and test sets
[js] basic syntax - for loop