当前位置:网站首页>[论文阅读] ACT: An Attentive Convolutional Transformer for Efficient Text Classification
[论文阅读] ACT: An Attentive Convolutional Transformer for Efficient Text Classification
2022-08-02 14:07:00 【lq_fly_pig】
一、前言
追一科技AAAI2021上的论文,主要是关于文本分类任务,论文地址:https://www.aaai.org/AAAI21Papers/AAAI-1396.LiP.pdf
二、主要思想
深度学习热火朝天的今天,nlp领域,Transformer结构的网络逐步取代RNN网络,前几年大火的CNN网络关注度也逐渐降低,由于其 不擅长于处理全局信息和长序列特征信息,恰恰这是Transformer的优点,善于处理长文本信息。作者基于CNN的优点(模型参数较小,推理速度较快),Transformer的优点(长序列信息处理),提出一种Attentive Convolutional Transformer (ACT) 方法,能够在保留顺序信息的同时有效地捕获本地和全局依赖信息,且加速模型的推理速度
三、论文试验结果
在多个文本分类数据集上与包括RNN、CNN以及Transformer等模型结构进行了对比,结论表明ACT在所有数据集上都获得了最好的表现(accuracy统计),右边是F1-score 的指标

对于模型大小和模型的推理加速也有实验结果:
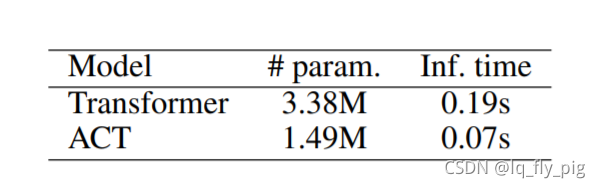
从上图中得到的信息是ACT的模型大小约为Transformer的三分之一,但是推理的速度则加快了一倍以上
论文中还给出了attention模式的对比,对比了ACT与transformer在attention可视化上的区别:

上面第一行为transformer结构的注意力可视化,下面低二行为ACT的注意力可视化。
可以看到transformer结构更加倾向于对更多的词进行关注,而ACT的关注点则更加集中与准确。
四、论文讲解
设置文本的输入长度为 ,词向量的维度为d,得到输入的词向量,Q = [
,词向量的维度为d,得到输入的词向量,Q = [ ,
, ,
, ,...,
,..., ]
]
(1). Local feature


 ,为第i 个token的编码,而d 则是编码的维度,token的编码可以采用经典方式获取,进一步设置卷积核参数,
,为第i 个token的编码,而d 则是编码的维度,token的编码可以采用经典方式获取,进一步设置卷积核参数, ![\large F=[f_{1},f_{2},f_{3},...,f_{m}]](http://img.inotgo.com/imagesLocal/202208/02/202208021402467909_7.gif) ,表示m个卷积核,其中
,表示m个卷积核,其中
 表示第i个卷积核,n 表示卷积核的宽度,使用 卷积F和文本Q 进行卷积计算:
表示第i个卷积核,n 表示卷积核的宽度,使用 卷积F和文本Q 进行卷积计算:

其中 * 表示卷积运算, , m表示卷积核的数量,
, m表示卷积核的数量, 表示 句子的长度,也就是token的长度,即表示 句子的长度,和textCNN 的操作类似。具体大家可以看看textCNN 的卷积过程。卷积过程,论文中指出的 第i个卷积核
表示 句子的长度,也就是token的长度,即表示 句子的长度,和textCNN 的操作类似。具体大家可以看看textCNN 的卷积过程。卷积过程,论文中指出的 第i个卷积核 在第j 个位置的卷积如下,卷积核的长度为n:
在第j 个位置的卷积如下,卷积核的长度为n:

然后计算对m个卷积核中每个卷积核的权重,即注意力,具体计算如下

解释下上面的公式,F表示原始的卷积核矩阵,卷积核大小为[d,n], 卷积核的个数为m,因此卷积核矩阵为[dxn,m] , M = [m,l] , l表示的是句子的长度 token 的长度,最终得到卷积核的加权后的特征表示信息:
![\large O=[o_{1},o_{2},o_{3},...,o_{l}] \in \mathbb{R}^{nd\times l}](http://img.inotgo.com/imagesLocal/202208/02/202208021402467909_18.gif)
需要注意的是,论文中没有使用 transformer中的常规的softmax的权重来进行加权,而是直接使用卷积后的数值对原始的卷积核 F 进行加权。这个表征可以看作是对捕获n-gram模式的卷积核的加权。因此,可以认为这个输出包含了文本的n-gram局部信息。
(2). Global feature
ACT还通过如下方式来进行全局特征的计算:

解释下上面的公式,F 表示卷积,其特征大小为![\large [n*d,l]](http://img.inotgo.com/imagesLocal/202208/02/202208021402467909_16.gif) , M 表示的特征大小为
, M 表示的特征大小为![\large [m,l]](http://img.inotgo.com/imagesLocal/202208/02/202208021402467909_4.gif)
maxpool(M) 表示的是每一行进行最大池化,最终的维度maxPool(M) = [n*d,1]
边栏推荐
猜你喜欢
随机推荐
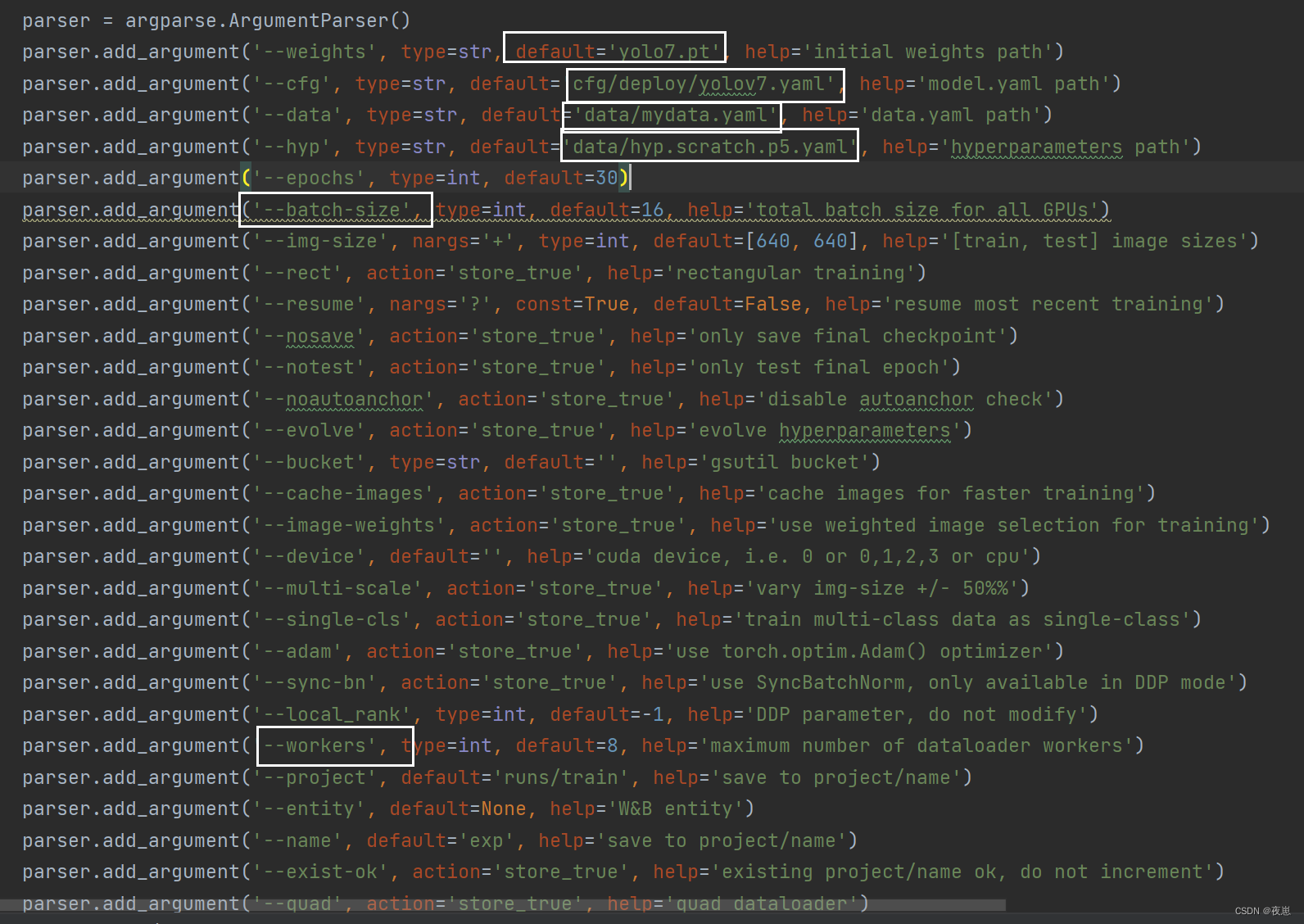
YOLOv7 uses cloud GPU to train its own dataset
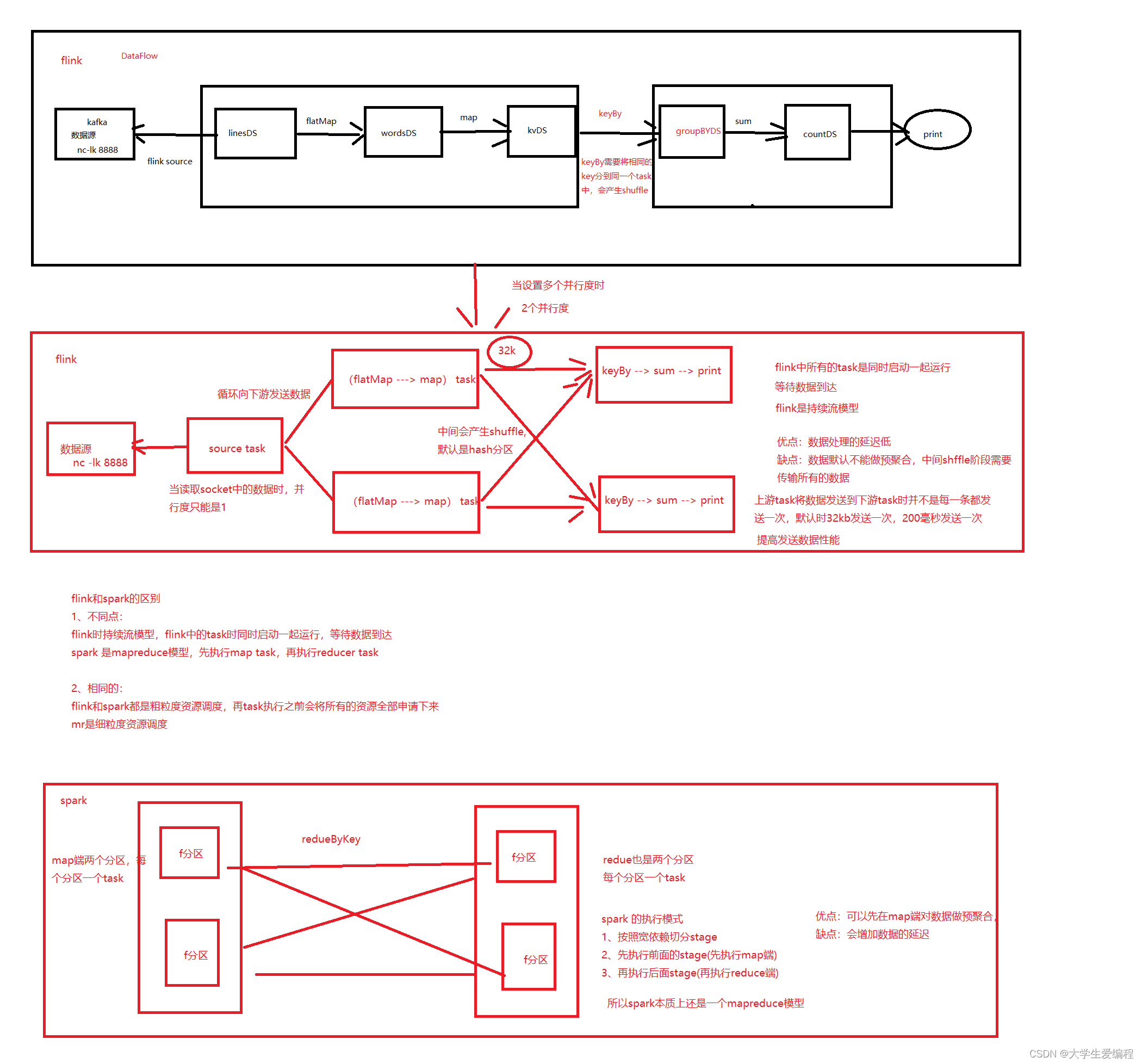
Flink前期代码结构
详解RecyclerView系列文章目录
7.如何给RecyclerView添加Click和LongClick事件
IllegalStateException: Room cannot verify the data integrity. Looks like you've changed schema but
数据乱码问题—更改mysql字符编码
统计偏科最严重的前100名学生
两个surfaceview的重叠效果类似直播效果中的视频和讲义实践
MongoDB Compass 安装与使用
Flink实现Exactly Once
1. What is RecyclerView
Must-know knowledge about disassembly
绕过正则实现SQL注入
线性代数期末复习存档
Spark_DSL
The Handler you really understand?
LLVM系列第十八章:写一个简单的IR处理流程Pass
C语言初级—常见问题(100~200素数,计算1+11+111+...,从键盘获取一个数并输出有几个位)
2022最新交规记忆重点
原码、反码、补码和移码