C语言 整型 和 浮点型 数据在内存中存储详解（内含原码反码补码，大小端存储等详解）

为了更加深刻的了解c语言内部数据的存储方式，首先我们要了解常用的几种类型和他们的大致分类。前言部分先给大家带来一些基础的知识介绍

前言：c语言数据类型介绍

char //字符数据类型
short //短整型
int //整形
long //长整型
long long //更长的整形
float //单精度浮点数
double //双精度浮点数

仔细观察可以发现
大致可以分为下面五类
1、整形家族：
如char、unsigned char、signed char、short、unsigned short [int]、signed short [int]、int、unsigned int、signed int、long、unsigned long [int]、signed long [int]等
2、浮点数家族：
如float、double等
3、构造类型：
如数组类型、结构体类型 struct、枚举类型 enum、联合类型 union等
4、指针类型：
如int pi、char pc、float pf、void pv等
5、空类型：
void 表示空类型（无类型）
（通常应用于函数的返回类型、函数的参数、指针类型）

有了上述的基础积累，我们下面进入正文

1. 整形在内存中的存储

空间的大小是根据不同的类型而决定的。
如int型占4个字节，那么这4个字节是如何分配的呢？
首先我们要了解原码，反码，补码

1.1原码、反码、补码的一些解释

   计算机中的整数有三种表示方法，即原码、反码和补码。
   三种表示方法均有符号位和数值位两部分，符号位都是用0表示“正”，用1表示“负”，而数值位负整数的三种表示方法各不相同。
原码

直接将二进制按照正负数的形式翻译成二进制就可以。
反码
将原码的符号位不变，其他位依次按位取反就可以得到了。
补码
反码+1就得到补码。
***注：***正数的原、反、补码都相同。
对于整形来说：数据存放内存中其实存放的是补码。
（因为在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。）

1.2、大小端存储模式

我们看下面一段简单的代码，利用上面的知识我们先自己判断16进制下a的值，再查看a在内存中是如何存储这些数的
十进制a=20
转换为二进制00000000000000000000000000010100
正整数原码反码补码一致，故存在计算机内存中的补码也是
00000000000000000000000000010100
转换成16进制（每四个转换一次）
00 00 00 14

我们现在查看a在vs下内存中是如何存储的

这里发现vs下存储的是14 00 00 00，与我们算出来的顺序是相反的，这是为什么呢？
这是因为不同编辑器有的是大端存储模式，有的是小端存储模式，下面我们开始介绍一下这两种存储模式：
什么大端小端：
大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中；
小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地址中。
那我们刚刚在vs中查看的内存信息就说明了vs下是小端存储模式

这里我们介绍一道判断当前编辑器下是大端存储还是小端存储的代码题

#include <stdio.h>
int check_sys()
{
    
 int i = 1;
 return (*(char *)&i);//把i强制类型转换成一个字节再查看i截断后地址的内容
 //如果是1，就是小端存储模式，反正为大端存储模式
}
int main()
{
    
 int ret = check_sys();
 if(ret == 1)
 {
    
 printf("小端\n");
 }
 else
 {
    
 printf("大端\n");
 }
 return 0; }

这是百度一道面试题哦，如有不懂还请留言！
下面我也给大家几道简单的代码进行练习，一般规律是写出该数据的原码反码补码，然后进行截断或者整型提升加以判断，如有不懂，欢迎留言！

1.
//输出什么？
#include <stdio.h>
int main()
{
    
    char a= -1;
    signed char b=-1;
    unsigned char c=-1;
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0; }

2.
#include <stdio.h>
int main()
{
    
    char a = -128;
    printf("%u\n",a);
    return 0; }

3.
#include <stdio.h>
int main()
{
    
    char a = 128;
    printf("%u\n",a);
    return 0; }

4.
int i= -20;
unsigned  int  j = 10;
printf("%d\n", i+j); 
//按照补码的形式进行运算，最后格式化成为有符号整数

5.
unsigned int i;
for(i = 9; i >= 0; i--) {
    
    printf("%u\n",i);
}

6.
int main()
{
    
    char a[1000];
    int i;
    for(i=0; i<1000; i++)
   {
    
        a[i] = -1-i;
   }
    printf("%d",strlen(a));
    return 0; }

7.
#include <stdio.h>
unsigned char i = 0;
int main()
{
    
    for(i = 0;i<=255;i++)
   {
    
        printf("hello world\n");
   }
    return 0; }

以上是整型数据在内存中的存储，下面我们讨论更为复杂的浮点数在内存中的存储方式

2、浮点数在内存中的存储

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：
(-1)^S * M * 2^E
(-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
M表示有效数字，大于等于1，小于2。
2^E表示指数位。

举个例子：

现在我们了解了浮点数如何转换成国际标准的方式，那么S M E如何在内存中存储呢？接下来看图：
（1）32位单精度浮点数

S中的0或者1存储在第一个比特位中，中间八个比特位存储E的数值，M的数值存在剩下的23个比特位中。
**但是！！！！**注意几个存储进去的要点
**1、**由于E可能会出现负数，32位平台下存储进去必须+127再转换成二进制存储进去！
**2、**由于M小数点前面恒为1，所以存储进去的只有小数点后面的数！

（2）64位双精度浮点数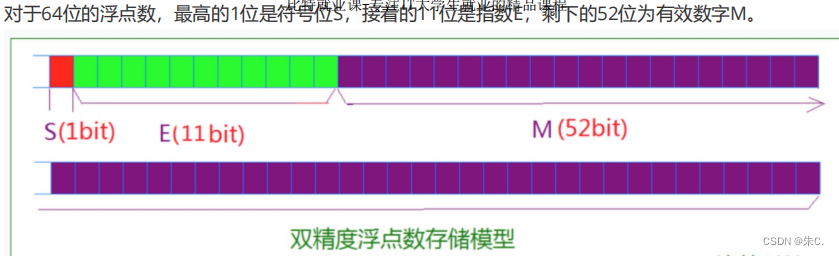

这里与32位不同的是E是加上1023后存储进去

下面我们讨论一下E存储进去的一些特殊情况：
1.E不全为0或不全为1
这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将
有效数字M前加上第一位的1。
比如：
0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000 ，则其二进
制表示形式为:
0 01111110 00000000000000000000000
2.E全为0
这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于
0的很小的数字。
3.E全为1
这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

最后我们用一道题目来让大家更加深入了解浮点数的存储

int main()
{
    
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 return 0; }

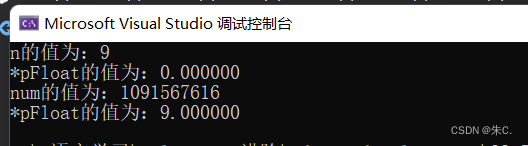
首先，9 -> 0000 0000 0000 0000 0000 0000 0000 1001
由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：
V=(-1)^0 * 0.00000000000000000001001×2^{(-126)=1.001×2}(-146)
显然，V是一个很小的接近于0的正数，所以用十进制小数表示就是0.000000。
再看例题的第二部分。
请问浮点数9.0，如何用二进制表示？还原成十进制又是多少？
首先，浮点数9.0等于二进制的1001.0，即1.001×2^3。
9.0 -> 1001.0 ->(-1)^01.00123 -> s=0, M=1.001,E=3+127=130
那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等于3+127=130， 即10000010。
所以，写成二进制形式，应该是s+E+M，即
0 10000010 001 0000 0000 0000 0000 0000
这个32位的二进制数，还原成十进制，正是 1091567616 。

以上是对整型和浮点型数据存储的详解，并且包含了大小端存储和原码反码补码等详解，如有不懂欢迎大家提问！