当前位置:网站首页>自然语言处理系列(一)——RNN基础
自然语言处理系列(一)——RNN基础
2022-07-02 09:42:00 【raelum】
注: 本文是总结性文章,叙述较为简洁,不适合初学者
一、为什么要有RNN?
普通的MLP无法处理序列信息(如文本、语音等),这是因为序列是不定长的,而MLP的输入层神经元个数是固定的。
二、RNN的结构
普通MLP的结构(以单隐层为例):
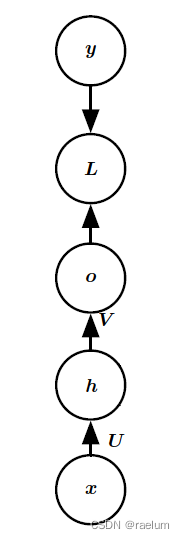
普通RNN(又称Vanilla RNN,接下来都将使用这一说法)的结构(在单隐层MLP的基础上进行改造):

即 t t t 时刻隐藏层接收的输入来自于 t − 1 t-1 t−1 时刻隐藏层的输出和 t t t 时刻的样例输入。用数学公式表示,就是
h ( t ) = tanh ( W h ( t − 1 ) + U x ( t ) + b ) , o ( t ) = V h ( t ) + c , y ^ ( t ) = softmax ( o ( t ) ) h^{(t)}=\tanh(Wh^{(t-1)}+Ux^{(t)}+b),\quad o^{(t)}=Vh^{(t)}+c,\quad \hat{y}^{(t)}=\text{softmax}(o^{(t)}) h(t)=tanh(Wh(t−1)+Ux(t)+b),o(t)=Vh(t)+c,y^(t)=softmax(o(t))
训练RNN的过程中,实际上就是在学习 U , V , W , b , c U,V,W,b,c U,V,W,b,c 这些参数。
正向传播后,我们需要计算损失,设时间步 t t t 处求得的损失为 L ( t ) = L ( t ) ( y ^ ( t ) , y ( t ) ) L^{(t)}=L^{(t)}(\hat{y}^{(t)},y^{(t)}) L(t)=L(t)(y^(t),y(t)),则总的损失为 L = ∑ t = 1 T L ( t ) L=\sum_{t=1}^T L^{(t)} L=∑t=1TL(t)。
2.1 BPTT
BPTT(BackPropagation Through Time),通过时间反向传播是RNN训练过程中的一个术语。因为正向传播时是沿着时间流逝的方向进行的,而反向传播则是逆着时间进行的。
为方便后续推导,我们先改进一下符号表述:
h ( t ) = tanh ( W h h h ( t − 1 ) + W x h x ( t ) + b ) , o ( t ) = W h o h ( t ) + c , y ^ ( t ) = softmax ( o ( t ) ) h^{(t)}=\tanh(W_{hh}h^{(t-1)}+W_{xh}x^{(t)}+b),\quad o^{(t)}=W_{ho}h^{(t)}+c,\quad \hat{y}^{(t)}=\text{softmax}(o^{(t)}) h(t)=tanh(Whhh(t−1)+Wxhx(t)+b),o(t)=Whoh(t)+c,y^(t)=softmax(o(t))
做一个水平方向的 concatenation: W = ( W h h , W x h ) W=(W_{hh},W_{xh}) W=(Whh,Wxh),为简便起见,省略偏置 b b b,则有
h ( t ) = tanh ( W ( h ( t − 1 ) x ( t ) ) ) h^{(t)}=\tanh\left(W \begin{pmatrix} h^{(t-1)} \\ x^{(t)} \end{pmatrix} \right) h(t)=tanh(W(h(t−1)x(t)))
,接下来我们将关注参数 W W W 的学习。
注意到
∂ h ( t ) ∂ h ( t − 1 ) = tanh ′ ( W h h h ( t − 1 ) + W x h x ( t ) ) W h h , ∂ L ∂ W = ∑ t = 1 T ∂ L ( t ) ∂ W \frac{\partial h^{(t)}}{\partial h^{(t-1)}}=\tanh'(W_{hh}h^{(t-1)}+W_{xh}x^{(t)})W_{hh},\quad \frac{\partial L}{\partial W}=\sum_{t=1}^T\frac{\partial L^{(t)}}{\partial W} ∂h(t−1)∂h(t)=tanh′(Whhh(t−1)+Wxhx(t))Whh,∂W∂L=t=1∑T∂W∂L(t)
从而
∂ L ( T ) ∂ W = ∂ L ( T ) ∂ h ( T ) ⋅ ∂ h ( T ) ∂ h ( T − 1 ) ⋯ ∂ h ( 2 ) ∂ h ( 1 ) ⋅ ∂ h ( 1 ) ∂ W = ∂ L ( T ) ∂ h ( T ) ⋅ ∏ t = 2 T ∂ h ( t ) ∂ h ( t − 1 ) ⋅ ∂ h ( 1 ) ∂ W = ∂ L ( T ) ∂ h ( T ) ⋅ ( ∏ t = 2 T tanh ′ ( W h h h ( t − 1 ) + W x h x ( t ) ) ) ⋅ W h h T − 1 ⋅ ∂ h ( 1 ) ∂ W \begin{aligned} \frac{\partial L^{(T)}}{\partial W}&=\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \frac{\partial h^{(T)}}{\partial h^{(T-1)}}\cdots \frac{\partial h^{(2)}}{\partial h^{(1)}}\cdot\frac{\partial h^{(1)}}{\partial W} \\ &=\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \prod_{t=2}^T\frac{\partial h^{(t)}}{\partial h^{(t-1)}}\cdot\frac{\partial h^{(1)}}{\partial W}\\ &=\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot \left(\prod_{t=2}^T\tanh'(W_{hh}h^{(t-1)}+W_{xh}x^{(t)})\right)\cdot W_{hh}^{T-1} \cdot\frac{\partial h^{(1)}}{\partial W}\\ \end{aligned} ∂W∂L(T)=∂h(T)∂L(T)⋅∂h(T−1)∂h(T)⋯∂h(1)∂h(2)⋅∂W∂h(1)=∂h(T)∂L(T)⋅t=2∏T∂h(t−1)∂h(t)⋅∂W∂h(1)=∂h(T)∂L(T)⋅(t=2∏Ttanh′(Whhh(t−1)+Wxhx(t)))⋅WhhT−1⋅∂W∂h(1)
因为 tanh ′ ( ⋅ ) \tanh'(\cdot) tanh′(⋅) 几乎总是小于 1 1 1 的,当 T T T 足够大时将会出现梯度消失现象。
假如不采用非线性的激活函数,为简便起见,不妨设激活函数为恒等映射 f ( x ) = x f(x)=x f(x)=x,于是有
∂ L ( T ) ∂ W = ∂ L ( T ) ∂ h ( T ) ⋅ W h h T − 1 ⋅ ∂ h ( 1 ) ∂ W \frac{\partial L^{(T)}}{\partial W}=\frac{\partial L^{(T)}}{\partial h^{(T)}}\cdot W_{hh}^{T-1} \cdot\frac{\partial h^{(1)}}{\partial W} ∂W∂L(T)=∂h(T)∂L(T)⋅WhhT−1⋅∂W∂h(1)
- 当 W h h W_{hh} Whh 的最大奇异值大于 1 1 1 时,会出现梯度爆炸。
- 当 W h h W_{hh} Whh 的最大奇异值小于 1 1 1 时,会出现梯度消失。
三、RNN的分类
按照输入和输出的结构可以对RNN进行如下分类:
- 1 vs N(vec2seq):Image Captioning;
- N vs 1(seq2vec):Sentiment Analysis;
- N vs M(seq2seq):Machine Translation;
- N vs N(seq2seq):Sequence Labeling(POS Tagging)

注意 1 vs 1 是传统的MLP。
若按照内部构造进行分类则会得到:
- RNN、Bi-RNN、…
- LSTM、Bi-LSTM、…
- GRU、Bi-GRU、…
四、Vanilla RNN的优缺点
优点:
- 可以处理不定长的序列;
- 计算时会考虑历史信息;
- 权重沿时间方向上是共享的;
- 模型大小不会随着输入大小增加而改变。
缺点:
- 计算效率低;
- 梯度会消失/爆炸(后续将知道,避免梯度爆炸可采用梯度裁剪,避免梯度消失可换用其他的RNN结构,如LSTM);
- 无法处理长序列(即不具备长记忆性);
- 无法利用未来的输入(Bi-RNN可解决)。
五、Bidirectional RNN
许多时候,我们要输出的 y ( t ) y^{(t)} y(t) 可能依赖于整个序列,因此需要使用双向RNN(BRNN)。BRNN结合了时间上从序列起点开始移动的RNN和从序列末尾开始移动的RNN。两个RNN互相独立不共享权重:
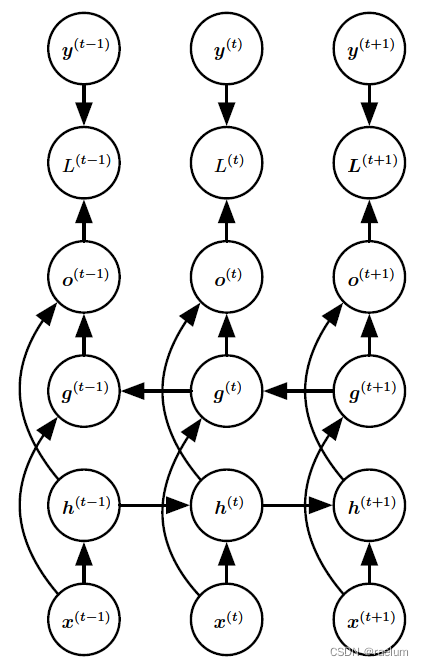
相应的计算方式变为:
h ( t ) = tanh ( W 1 h ( t − 1 ) + U 1 x ( t ) + b 1 ) g ( t ) = tanh ( W 2 h ( t − 1 ) + U 2 x ( t ) + b 2 ) o ( t ) = V ( h ( t ) ; g ( t ) ) + c y ^ ( t ) = softmax ( o ( t ) ) \begin{aligned} &h^{(t)}=\tanh(W_1h^{(t-1)}+U_1x^{(t)}+b_1) \\ &g^{(t)}=\tanh(W_2h^{(t-1)}+U_2x^{(t)}+b_2) \\ &o^{(t)}=V(h^{(t)};g^{(t)})+c \\ &\hat{y}^{(t)}=\text{softmax}(o^{(t)}) \\ \end{aligned} h(t)=tanh(W1h(t−1)+U1x(t)+b1)g(t)=tanh(W2h(t−1)+U2x(t)+b2)o(t)=V(h(t);g(t))+cy^(t)=softmax(o(t))
其中 ( h ( t ) ; g ( t ) ) (h^{(t)};g^{(t)}) (h(t);g(t)) 代表将两个列向量 h ( t ) h^{(t)} h(t) 和 g ( t ) g^{(t)} g(t) 进行纵向连接。
事实上,若将 V V V 按列分块,则上述的第三个等式还可写成:
o ( t ) = V ( h ( t ) ; g ( t ) ) + c = ( V 1 , V 2 ) ( h ( t ) g ( t ) ) + c = V 1 h ( t ) + V 2 g ( t ) + c o^{(t)}=V(h^{(t)};g^{(t)})+c= (V_1,V_2) \begin{pmatrix} h^{(t)} \\ g^{(t)} \end{pmatrix}+c=V_1h^{(t)}+V_2g^{(t)}+c o(t)=V(h(t);g(t))+c=(V1,V2)(h(t)g(t))+c=V1h(t)+V2g(t)+c
训练 BRNN 的过程实际就是在学习 U 1 , U 2 , V , W 1 , W 2 , b 1 , b 2 , c U_1,U_2,V,W_1,W_2,b_1,b_2,c U1,U2,V,W1,W2,b1,b2,c 这些参数。
六、Stacked RNN
堆叠RNN又称多层RNN或深度RNN,即由多个隐藏层组成。以双隐层单向RNN为例,其结构如下:
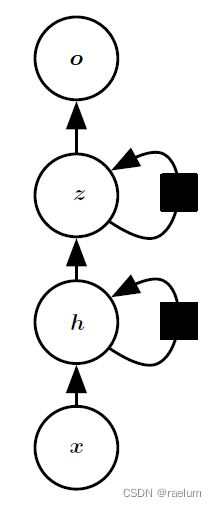
相应的计算过程如下:
h ( t ) = tanh ( W h h h ( t − 1 ) + W x h x ( t ) + b h ) z ( t ) = tanh ( W z z z ( t − 1 ) + W h z h ( t ) + b z ) o ( t ) = W z o z ( t ) + b o y ^ ( t ) = softmax ( o ( t ) ) \begin{aligned} &h^{(t)}=\tanh(W_{hh}h^{(t-1)}+W_{xh}x^{(t)}+b_h) \\ &z^{(t)}=\tanh(W_{zz}z^{(t-1)}+W_{hz}h^{(t)}+b_z) \\ &o^{(t)}=W_{zo}z^{(t)}+b_o \\ &\hat{y}^{(t)}=\text{softmax}(o^{(t)}) \\ \end{aligned} h(t)=tanh(Whhh(t−1)+Wxhx(t)+bh)z(t)=tanh(Wzzz(t−1)+Whzh(t)+bz)o(t)=Wzoz(t)+boy^(t)=softmax(o(t))
边栏推荐
- [visual studio 2019] create and import cmake project
- Implementation of address book (file version)
- PX4 Position_Control RC_Remoter引入
- MySQL stored procedure cursor traversal result set
- How to Create a Beautiful Plots in R with Summary Statistics Labels
- Tdsql | difficult employment? Tencent cloud database micro authentication to help you
- 通讯录的实现(文件版本)
- 多文件程序X32dbg动态调试
- Fabric. JS 3 APIs to set canvas width and height
- Wechat applet uses Baidu API to achieve plant recognition
猜你喜欢
PYQT5+openCV项目实战:微循环仪图片、视频记录和人工对比软件(附源码)

SVO2系列之深度滤波DepthFilter
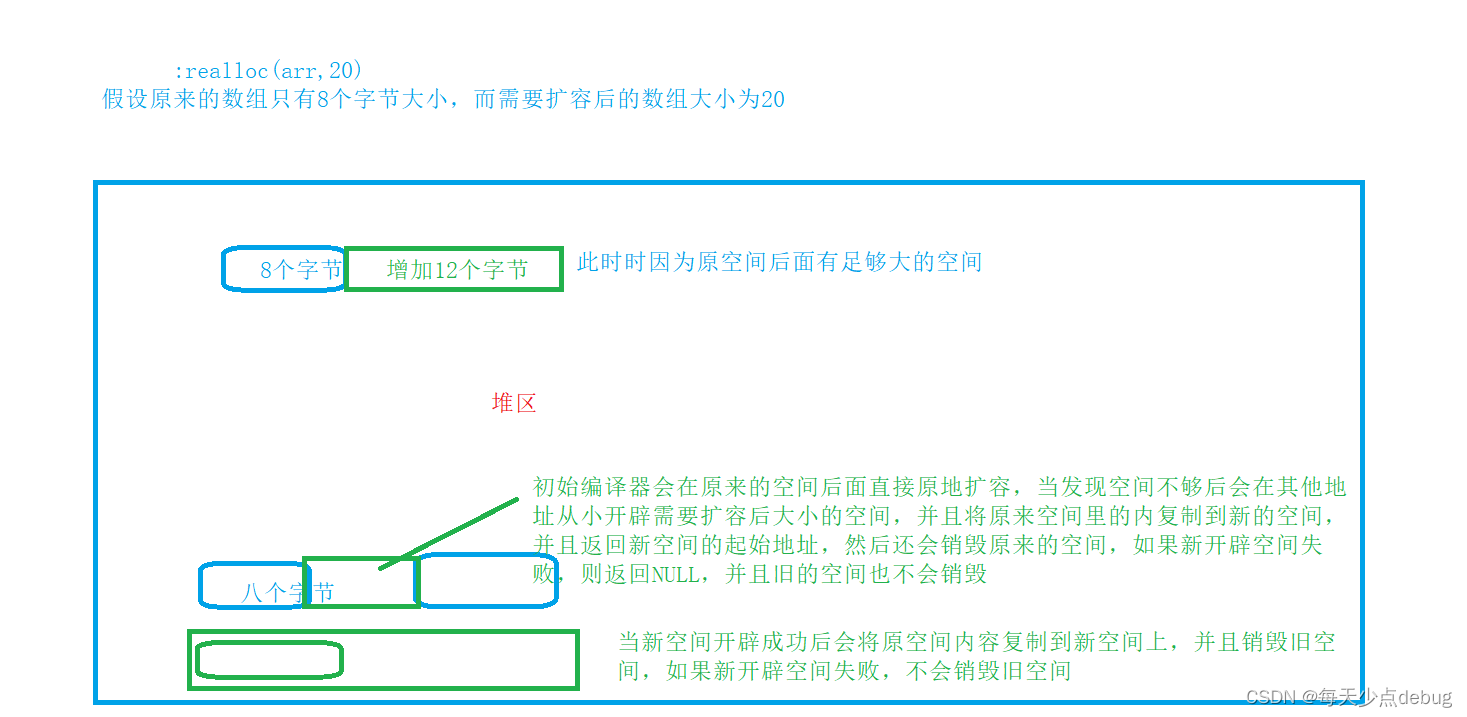
Dynamic memory (advanced 4)

可昇級合約的原理-DelegateCall
How to Easily Create Barplots with Error Bars in R
How to Visualize Missing Data in R using a Heatmap

GGPUBR: HOW TO ADD ADJUSTED P-VALUES TO A MULTI-PANEL GGPLOT

GGPlot Examples Best Reference
A sharp tool for exposing data inconsistencies -- a real-time verification system

PgSQL string is converted to array and associated with other tables, which are displayed in the original order after matching and splicing
随机推荐
行业的分析
CMake交叉编译
行業的分析
Attribute acquisition method and operation notes of C # multidimensional array
R HISTOGRAM EXAMPLE QUICK REFERENCE
ESP32音频框架 ESP-ADF 添加按键外设流程代码跟踪
GGPUBR: HOW TO ADD ADJUSTED P-VALUES TO A MULTI-PANEL GGPLOT
Programmer growth Chapter 6: how to choose a company?
PyTorch中repeat、tile与repeat_interleave的区别
基于 Openzeppelin 的可升级合约解决方案的注意事项
Order by injection
Redis exceeds the maximum memory error oom command not allowed when used memory & gt; ' maxmemory'
Precautions for scalable contract solution based on openzeppelin
[multithreading] the main thread waits for the sub thread to finish executing, and records the way to execute and obtain the execution result (with annotated code and no pit)
BEAUTIFUL GGPLOT VENN DIAGRAM WITH R
How to Create a Beautiful Plots in R with Summary Statistics Labels
【2022 ACTF-wp】
Cluster Analysis in R Simplified and Enhanced
Log4j2
自然语言处理系列(三)——LSTM