当前位置：网站首页>自然语言处理系列（三）——LSTM

自然语言处理系列（三）——LSTM

2022-07-02 09:42:00 【raelum】

注： 本文是总结性文章，不适合初学者

目录

一、结构比较

只考虑单隐层单向的RNN，忽略输出层，首先看Vanilla RNN中一个cell的结构：

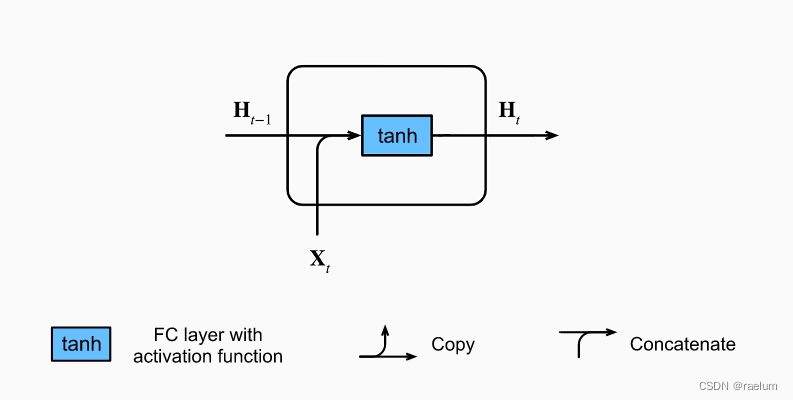
在这里插入图片描述

其计算过程为（设批量大小为 N N N，隐层结点个数为 h h h，输入特征数为 d d d）：

H t = tanh ⁡ ( X t W x h + H t − 1 W h h + b h ) {\bf H}_t=\tanh({\bf X}_t{\bf W}_{xh}+{\bf H}_{t-1}{\bf W}_{hh}+{\boldsymbol b}_h) Ht​=tanh(Xt​Wxh​+Ht−1​Whh​+bh​)

其中各参数的形状为：

  • H t , H t − 1 {\bf H}_t,{\bf H}_{t-1} Ht​,Ht−1​： N × h N\times h N×h；
  • X t {\bf X}_t Xt​： N × d N\times d N×d；
  • W x h {\bf W}_{xh} Wxh​： d × h d\times h d×h；
  • W h h {\bf W}_{hh} Whh​： h × h h\times h h×h；
  • b h {\boldsymbol b}_{h} bh​： 1 × h 1\times h 1×h。

在计算时， b h {\boldsymbol b}_{h} bh​ 将利用广播机制从上往下复制成 N × h N\times h N×h 的形状。

LSTM中一个cell的结构：

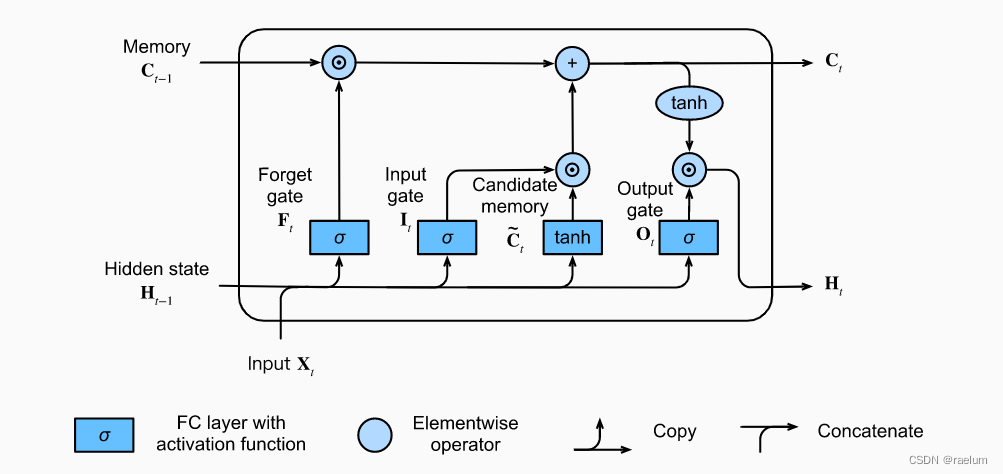
在这里插入图片描述

其计算过程为（设 σ ( ⋅ ) \sigma(\cdot) σ(⋅) 代表 Sigmoid ( ⋅ ) \text{Sigmoid}(\cdot) Sigmoid(⋅)）：

I t = σ ( X t W x i + H t − 1 W h i + b i ) F t = σ ( X t W x f + H t − 1 W h f + b f ) O t = σ ( X t W x o + H t − 1 W h o + b o ) C ~ t = tanh ⁡ ( X t W x c + H t − 1 W h c + b c ) C t = F t ⊙ C t − 1 + I t ⊙ C ~ t H t = O t ⊙ tanh ⁡ ( C t ) \begin{aligned} {\bf I}_t&=\sigma({\bf X}_t{\bf W}_{xi}+{\bf H}_{t-1}{\bf W}_{hi}+{\boldsymbol b}_i) \\ {\bf F}_t&=\sigma({\bf X}_t{\bf W}_{xf}+{\bf H}_{t-1}{\bf W}_{hf}+{\boldsymbol b}_f) \\ {\bf O}_t&=\sigma({\bf X}_t{\bf W}_{xo}+{\bf H}_{t-1}{\bf W}_{ho}+{\boldsymbol b}_o) \\ \tilde{ {\bf C}}_t&=\tanh({\bf X}_t{\bf W}_{xc}+{\bf H}_{t-1}{\bf W}_{hc}+{\boldsymbol b}_c) \\ {\bf C}_t&={\bf F}_t \odot{\bf C}_{t-1}+{\bf I}_t\odot \tilde{ {\bf C}}_t \\ {\bf H}_t&={\bf O}_t\odot \tanh({\bf C}_t) \\ \end{aligned} It​Ft​Ot​C~t​Ct​Ht​​=σ(Xt​Wxi​+Ht−1​Whi​+bi​)=σ(Xt​Wxf​+Ht−1​Whf​+bf​)=σ(Xt​Wxo​+Ht−1​Who​+bo​)=tanh(Xt​Wxc​+Ht−1​Whc​+bc​)=Ft​⊙Ct−1​+It​⊙C~t​=Ot​⊙tanh(Ct​)​

其中 ⊙ \odot ⊙ 是矩阵的 Hadamard 积，各参数的形状如下：

  • H t , H t − 1 {\bf H}_t,{\bf H}_{t-1} Ht​,Ht−1​、 I t , F t , O t {\bf I}_t,{\bf F}_t,{\bf O}_t It​,Ft​,Ot​、 C ~ t , C t , C t − 1 \tilde{ {\bf C}}_t,{\bf C}_t,{\bf C}_{t-1} C~t​,Ct​,Ct−1​： N × h N\times h N×h；
  • X t {\bf X}_t Xt​： N × d N\times d N×d；
  • W x i , W x f , W x o , W x c {\bf W}_{xi},{\bf W}_{xf},{\bf W}_{xo},{\bf W}_{xc} Wxi​,Wxf​,Wxo​,Wxc​： d × h d\times h d×h；
  • W h i , W h f , W h o , W h c {\bf W}_{hi},{\bf W}_{hf},{\bf W}_{ho},{\bf W}_{hc} Whi​,Whf​,Who​,Whc​： h × h h\times h h×h；
  • b i , b f , b o , b c {\boldsymbol b}_{i},{\boldsymbol b}_{f},{\boldsymbol b}_{o},{\boldsymbol b}_{c} bi​,bf​,bo​,bc​： 1 × h 1\times h 1×h

二、LSTM基础

LSTM一共有三个门： I t , F t , O t {\bf I}_t,{\bf F}_t,{\bf O}_t It​,Ft​,Ot​ 分别代表输入门、遗忘门和输出门。输入门用来控制采用多少来自 C ~ t \tilde{ {\bf C}}_t C~t​ 的新数据，遗忘门用来控制保留多少 C t − 1 {\bf C}_{t-1} Ct−1​ 的内容，输出门用来控制向下一个时间步传递多少记忆信息。

对于LSTM，只考虑 batch_first=True 的情形，输入数据的形状为 L × N × d L\times N\times d L×N×d。此外还需输入 H 0 {\bf H}_0 H0​ 和 C 0 {\bf C}_0 C0​，其形状均为 1 × N × h 1\times N\times h 1×N×h。

LSTM 在所有时间步上的输出为 [ H 1 , H 2 , ⋯   , H L ] L × N × h [{\bf H}_1,{\bf H}_2,\cdots,{\bf H}_L]_{L\times N\times h} [H1​,H2​,⋯,HL​]L×N×h​ 和 [ C 1 , C 2 , ⋯   , C L ] L × N × h [{\bf C}_1,{\bf C}_2,\cdots,{\bf C}_L]_{L\times N\times h} [C1​,C2​,⋯,CL​]L×N×h​。其中 H t {\bf H}_t Ht​ 代表 t t t 时刻的隐状态， C t {\bf C}_t Ct​ 代表 t t t 时刻的记忆。

三、从零开始搭建LSTM

不考虑隐层和输出层之间的参数，可以看出LSTM需要学习的参数一共有 4 4 4 组，即： ( W x ∗ , W h ∗ , b ∗ ) ,    where    ∗ = i , f , o , c ({\bf W}_{x*},{\bf W}_{h*},{\boldsymbol b}_{*}),\; \text{where}\;*=i,f,o,c (Wx∗​,Wh∗​,b∗​),where∗=i,f,o,c。因此我们可以按组去初始化相应的参数。

LSTM需要学习的参数一共有 3 × 4 = 12 3\times4=12 3×4=12 个，相比Vanilla RNN的 3 3 3 个参数多了很多。

首先导入本文代码涉及到的所有包：

import math
import string
import numpy as np
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.functional as F

我们定义一个函数来初始化一组的参数。注意到每一组参数的形状为 ( d × h , h × h , 1 × h ) (d\times h,h\times h,1\times h) (d×h,h×h,1×h)：

def init_group_params(input_size, hidden_size):
    std = math.sqrt(2 / (input_size + hidden_size))
    return nn.Parameter(torch.randn(input_size, hidden_size) * std), \
           nn.Parameter(torch.randn(hidden_size, hidden_size) * std), \
           nn.Parameter(torch.randn(1, hidden_size) * std)

接下来搭建LSTM（模仿 nn.LSTM，即不包含隐层和输出层之间的参数）:

class LSTM(nn.Module):

    def __init__(self, input_size, hidden_size):
        super().__init__()
        self.W_xi, self.W_hi, self.b_i = init_group_params(input_size, hidden_size)
        self.W_xf, self.W_hf, self.b_o = init_group_params(input_size, hidden_size)
        self.W_xo, self.W_ho, self.b_f = init_group_params(input_size, hidden_size)
        self.W_xc, self.W_hc, self.b_c = init_group_params(input_size, hidden_size)

    def forward(self, inputs, h_0, c_0):
        L, N, d = inputs.shape
        H, C = h_0[0], c_0[0]
        outputs = []
        for t in range(L):
            X = inputs[t]
            I = torch.sigmoid(X @ self.W_xi + H @ self.W_hi + self.b_i)
            F = torch.sigmoid(X @ self.W_xf + H @ self.W_hf + self.b_f)
            O = torch.sigmoid(X @ self.W_xo + H @ self.W_ho + self.b_o)
            C_temp = torch.tanh(X @ self.W_xc + H @ self.W_hc + self.b_c)
            C = F * C + I * C_temp
            H = O * torch.tanh(C)
            outputs.append(H)
        h_n, c_n = H.unsqueeze(0), C.unsqueeze(0)
        outputs = torch.cat(outputs, 0).unsqueeze(1)
        return outputs, h_n, c_n

最后搭建模型，此时需要加上线性层（输出层）：

class Model(nn.Module):

    def __init__(self, input_size, hidden_size, output_size):
        super().__init__()
        self.lstm = LSTM(input_size, hidden_size)
        self.linear = nn.Linear(hidden_size, output_size)

    def forward(self, x):
        # 全零初始化h_0和c_0
        _, h_n, _ = self.lstm(x, torch.zeros(1, x.shape[1], self.linear.in_features).to(device),
                              torch.zeros(1, x.shape[1], self.linear.in_features).to(device))
        return self.linear(h_n[0])

四、测试我们的LSTM

为了验证搭建好的LSTM是正确的模型，我们需要用它来完成一个任务。

4.1 字符预测任务

通俗点来讲，即给定一个单词（长度为 n n n），当模型读取了前 n − 1 n-1 n−1 个字母后，它能够准确地预测出最后一个字母。例如，对于单词 machine，当模型读取完 machin 后，它应当给出预测结果：e。

需要注意的是，字符预测任务并不是完美的。例如给定前两个字母 be，第三个字母无论是 e 还是 t 都能构成一个单词，而测试集是有限的，可能只有唯一的答案。

我们使用单词数据集（下载地址），其中训练集包含了 8000 个单词，测试集包含了 2000 个单词，且训练集和测试集没有重合。

4.2 数据预处理

LSTM无法直接识别字母，因此需要先将单个字母转化成张量（one-hot编码）：

def letter2tensor(letter):
    letter_idx = torch.tensor(string.ascii_lowercase.index(letter))
    return F.one_hot(letter_idx, num_classes=len(string.ascii_lowercase))

然后再创建一个函数用于将整个单词转化成对应的张量（这里我们将一个单词视为一个 batch，因此形状为 L × 1 × d L\times1\times d L×1×d，其中 d = 26 d=26 d=26， L L L 是单词的长度）:

def word2tensor(word):
    result = torch.zeros(len(word), len(string.ascii_lowercase))
    for i in range(len(word)):
        result[i] = letter2tensor(word[i])
    return result.unsqueeze(1)

例如：

print(word2tensor('cat'))
# tensor([[[0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

# [[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 0., 0., 0., 0., 0., 0., 0.]],

# [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 1., 0., 0., 0., 0., 0., 0.]]])

读取训练集和测试集：

with open('words/train.txt') as f:
    train_data = f.read().strip().split('\n')
    
with open('words/test.txt') as f:
    test_data = f.read().strip().split('\n')
    
print(train_data[0], test_data[1])
# clothe trend

此外，为了保证结果的可复现性，我们还需设置种子：

def setup_seed(seed):
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)

4.3 训练与测试

我们将在训练集上训练 5 个epoch，因为 batch_size=1，所以每隔 800 个 Iteration 输出一次损失并计算此时模型在测试集上的准确率，最后绘制相应的曲线。

setup_seed(42)

device = 'cuda' if torch.cuda.is_available() else 'cpu'
# 实际上相当于26分类任务，所以输出层神经元个数是26
model = Model(26, 64, 26)
model.to(device)

LR = 7e-3  # 学习率
EPOCHS = 5  # 多少个epoch
INTERVAL = 800  # 多少个iteration输出一次

critertion = nn.CrossEntropyLoss()
# 采用SGD优化器会出现测试集精度不变的情况
optimizer = torch.optim.Adam(model.parameters(), lr=LR, weight_decay=3e-4)

train_loss = []
test_acc = []
avg_train_loss = 0  # 训练集平均损失
correct = 0  # 模型在测试集上预测正确的个数

for epoch in range(EPOCHS):
    print(f'Epoch {
      epoch+1}')
    print('-' * 62)
    for iteration in range(len(train_data)):
        full_word = train_data[iteration]
        # 读取的是前n-1个字母，最后一个字母用作target
        X = word2tensor(full_word[:-1]).to(device)
        target = torch.tensor([string.ascii_lowercase.index(full_word[-1])]).to(device)

        # 正向传播
        output = model(X)
        loss = critertion(output, target)
        avg_train_loss += loss

        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # 每隔800个iteration输出一次损失并计算模型在测试集上的准确率
        if (iteration + 1) % INTERVAL == 0:
            avg_train_loss /= INTERVAL
            train_loss.append(avg_train_loss.item())

            # 计算模型在测试集上的预测准确率
            with torch.no_grad():
                for test_word in test_data:
                    X = word2tensor(test_word[:-1]).to(device)
                    target = torch.tensor(string.ascii_lowercase.index(test_word[-1])).to(device)
                    pred = model(X)
                    correct += (pred.argmax() == target).sum().item()
                acc = correct / len(test_data)
                test_acc.append(acc)

            print(
                f'Iteration: [{
      iteration + 1:04}/{
      len(train_data)}] | Train Loss: {
      avg_train_loss:.4f} | Test Acc: {
      acc:.4f}'
            )
            avg_train_loss, correct = 0, 0
    print()

这里仅展示最后一个 epoch 的输出：

Epoch 5
--------------------------------------------------------------
Iteration: [0800/8000] | Train Loss: 1.2918 | Test Acc: 0.6000
Iteration: [1600/8000] | Train Loss: 1.1903 | Test Acc: 0.5910
Iteration: [2400/8000] | Train Loss: 1.2615 | Test Acc: 0.6075
Iteration: [3200/8000] | Train Loss: 1.2236 | Test Acc: 0.6015
Iteration: [4000/8000] | Train Loss: 1.2355 | Test Acc: 0.5925
Iteration: [4800/8000] | Train Loss: 1.1314 | Test Acc: 0.6050
Iteration: [5600/8000] | Train Loss: 1.2172 | Test Acc: 0.6045
Iteration: [6400/8000] | Train Loss: 1.1808 | Test Acc: 0.6140
Iteration: [7200/8000] | Train Loss: 1.2092 | Test Acc: 0.6185
Iteration: [8000/8000] | Train Loss: 1.1845 | Test Acc: 0.6040

绘制曲线：

step = INTERVAL / len(train_data)
plt.plot(np.arange(step, EPOCHS + step, step), train_loss, label="train loss")
plt.plot(np.arange(step, EPOCHS + step, step), test_acc, label="test acc")
plt.legend(loc="best", fontsize=12)
plt.xlabel('epoch')
plt.show()

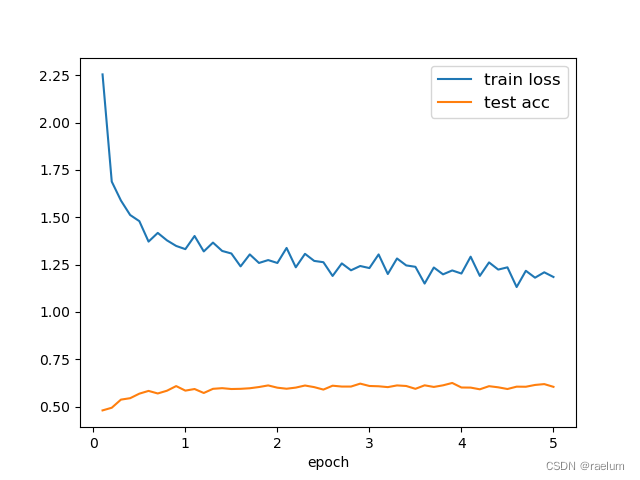
在这里插入图片描述

从上图可以看出，模型在测试集上的预测准确率趋于 0.6 0.6 0.6，原因可能有如下几点：

  • 数据集的质量不佳；
  • 数据集过于简单，LSTM出现了过拟合；
  • 我们的任务不够 “自洽”。
原网站

版权声明
本文为[raelum]所创，转载请带上原文链接，感谢
https://raelum.blog.csdn.net/article/details/125411349

边栏推荐

猜你喜欢

随机推荐