数据的存储

一、数据类型介绍

char           //字符数据类型 1
short          //短整型 2
int            //整形 4
long           //长整型 4(32位)/8（64位）
long long      //更长的整形 8 C99
float          //单精度浮点数 4
double         //双精度浮点数 8

类型的意义 :

1. 使用这个类型开辟内存空间的大小（大小决定了使用范围）。
2. 看待内存空间的视角不同。

1.1 类型的基本归类

（1） 整形家族

（2）浮点型家族

（3）构造类型

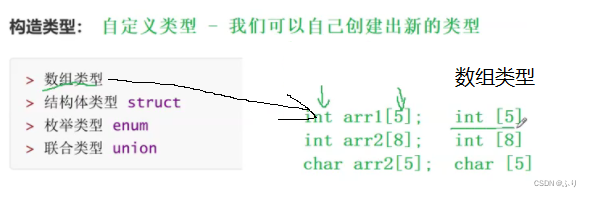
注 ： 其余的稍后讲解

（4）指针类型

（5）空类型

1. void 表示空类型（无类型）
2. 通常应用于函数的返回类型、函数的参数、指针类型

#include <stdio.h>
//第一个 void 表示函数不会返回值 (函数返回类型)
//第二个 void 表示函数不需要任何参数 （函数参数类型）
void test(void)
{
    
	printf("hehe\n");
}
int main()
{
    
	printf("hehehe\n");
	test();
	return 0;
}

二、整形在内存中的存储

一个变量的创建是要在内存中开辟空间的。空间的大小是根据不同的类型而决定的。

#include <stdio.h>

//数值有不同的表示形式
//2进制
//8进制
//10进制
//16进制
//十进制的21
//0b10101
//025
//21
//0x1

int main()
{
    
	int a = 20;
	int b = -10;
	  
	return 0;
}

2.1 原码、反码、补码

#include <stdio.h>

//数值有不同的表示形式
//2进制
//8进制
//10进制
//16进制
//十进制的21
//0b10101
//025
//21
//0x1

//
//整数的2进制有三种表示形式
//1. 正的整数， 原码、反码、补码相同
//2. 负的整数， 原码、反码、补码都需要计算
//原码 ： 直接通过正负的形式写出的二进制序列就是原码
//反码 ： 原码的符号位不变，其他位按位取反
//补码 ： 反码 + 1 就是补码
//


int main()
{
    
	int a = 20;
	//20
	//0000 0000 0000 0000 0000 0000 0001 0100
	//0x00 00 00 14 十六进制
	int b = -10;
	//-10
	//1000 0000 0000 0000 0000 0000 0000 1010 -- 原码
	// 0x80 00 00 00 0a
	//1111 1111 1111 1111 1111 1111 1111 0101 -- 反码
	// 0xfffffff5
	//1111 1111 1111 1111 1111 1111 1111 1010 -- 补码
	//0xfffffff6 
	return 0;
}

&a

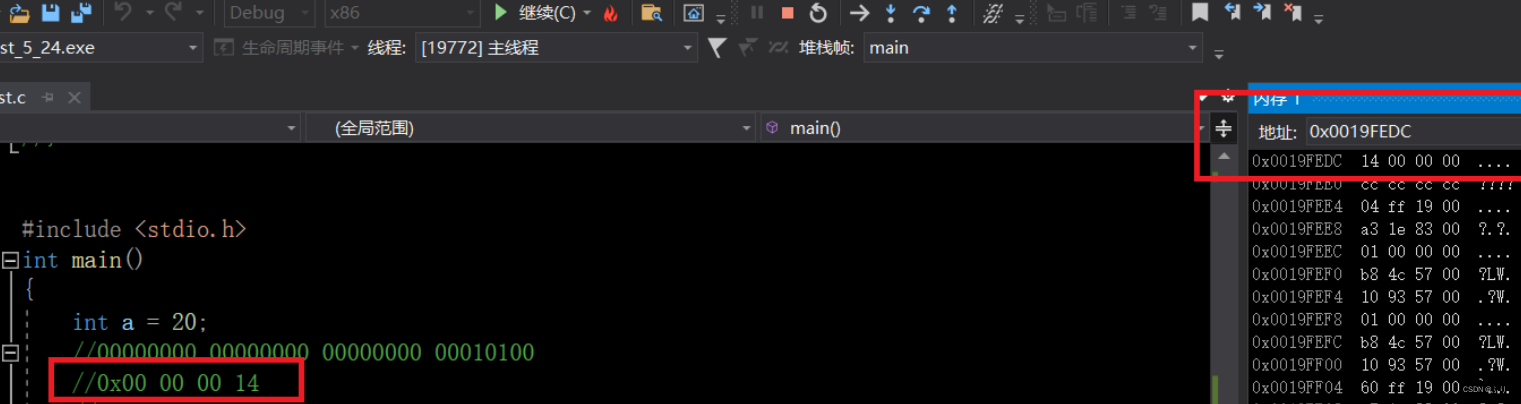
我们可以看到对于a和b分别存储的是补码。但是我们发现顺序有点不对劲。
这是又为什么？

2.2 大小端介绍

什么大端小端：

1. 大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址中；
2. 小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地
   址中。

为什么会有大小端

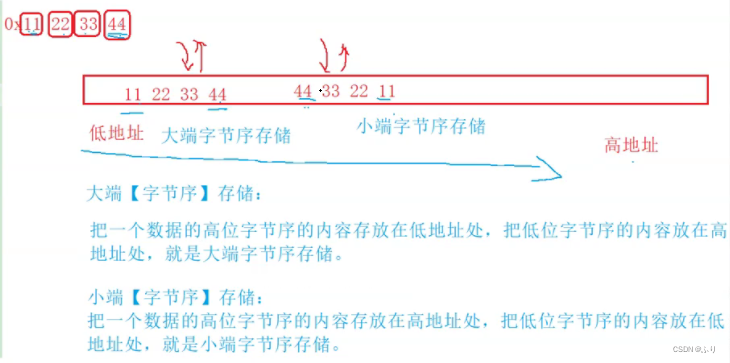
注 ：0x 11 22 33 44 高位是 11 ，低位是 44 ，类似于 150 ，高位是 1
低位是 0

百度2015年系统工程师笔试题：

//请简述大端字节序和小端字节序的概念，
//设计一个小程序来判断当前机器的字节序。（10分）

#include <stdio.h>
int check()
{
    
	int i = 1;
	//&i 获得首地址 ，强制类型转换成 char* 类型然后解引用得到前面是 00 还是 01
	return (*(char*)&i);
}
int main()
{
    
	int ret = check();
	if (ret == 1)
	{
    
		printf("小端\n");
	}
	else
	{
    
		printf("大端\n");
	}
	return 0;
}

2.4 练习

一、

//输出什么？
#include <stdio.h>
int main()
{
    
    char a= -1;
    signed char b=-1;
    unsigned char c=-1;
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0; 
}

二、

2.
#include <stdio.h>
int main()
{
    
    char a = -128;
    printf("%u\n",a);
    return 0; 
}

三、

#include <stdio.h>
int main()
{
    
    char a = 128;
    printf("%u\n",a);
    printf("%d\n", a);
    return 0;
 }

四、

#include <stdio.h>
int main()
{
    
	int i = -20;
	unsigned int j = 10;
	return 0;
}

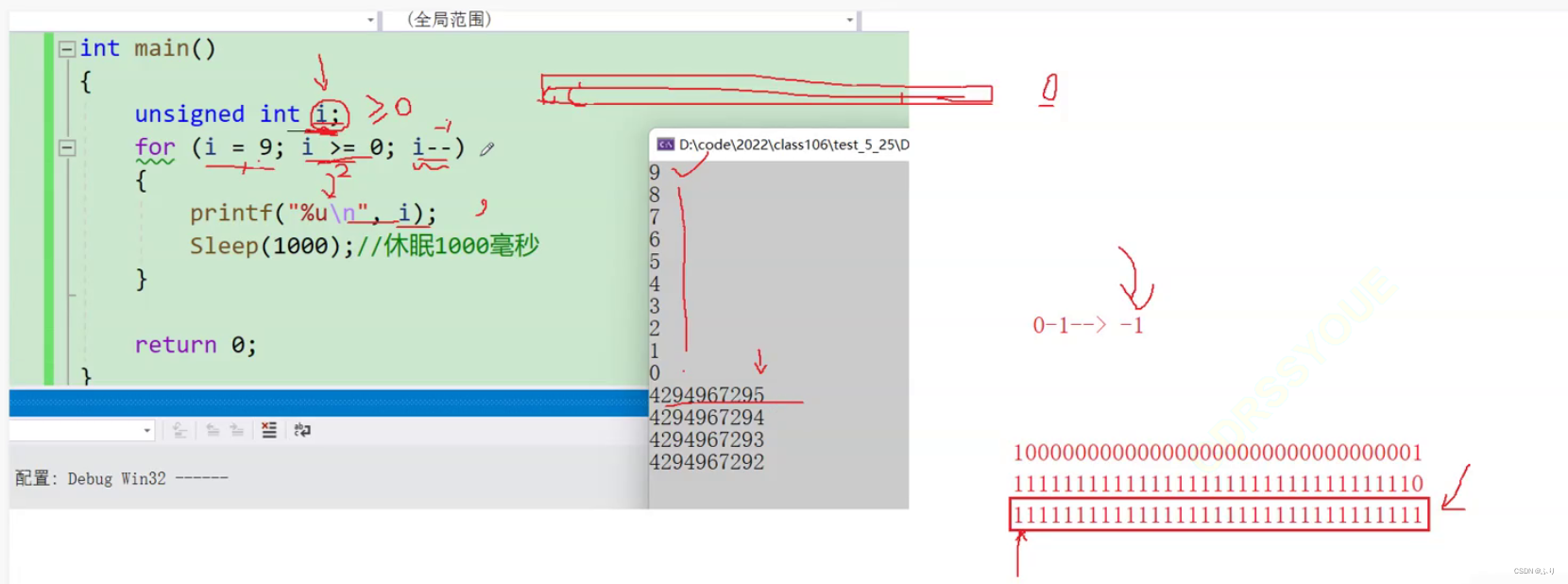
五、

#include <stdio.h>
#include <windows.h>
int main()
{
    
	unsigned int i;
	for (i = 9; i >= 0; i--) 
	{
    
		printf("%u\n", i);
		Sleep(1000);
	}
	return 0;
}

六、

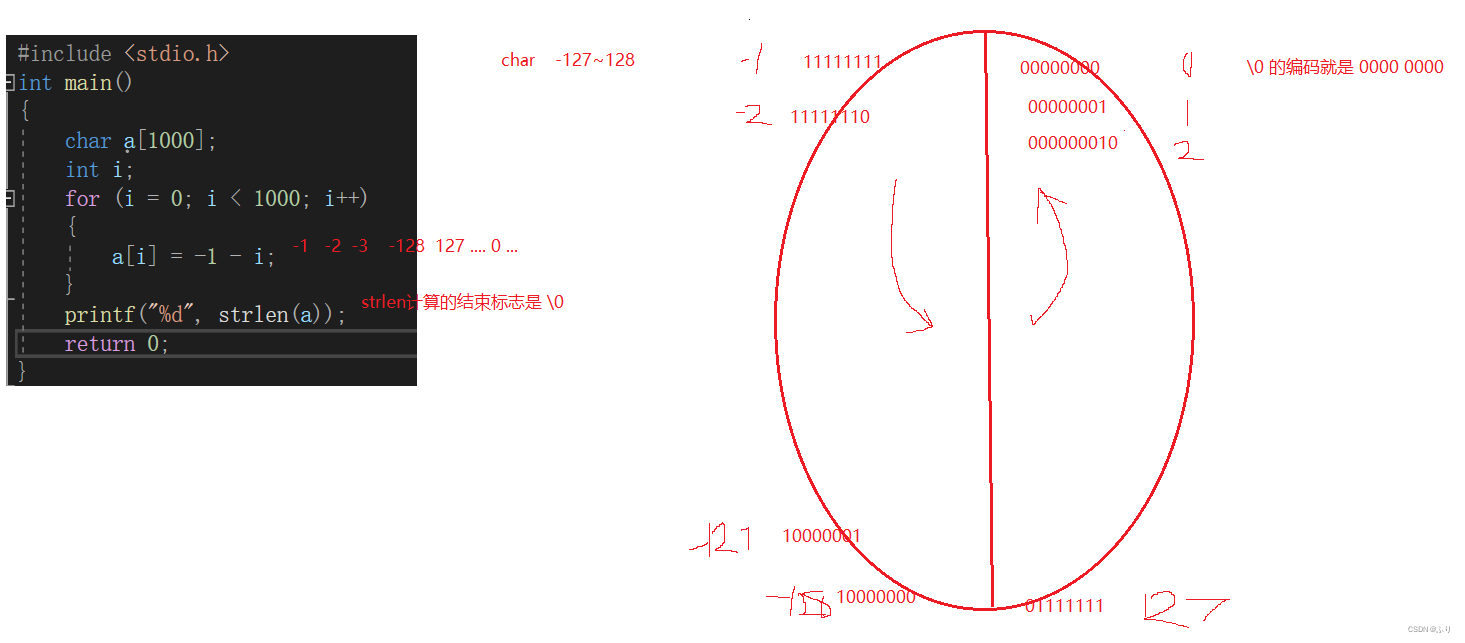
#include <stdio.h>
int main()
{
    
	char a[1000];
	int i;
	for (i = 0; i < 1000; i++)
	{
    
		a[i] = -1 - i;
	}
	printf("%d", strlen(a));
	return 0;
}

七、

#include <stdio.h>
unsigned char i = 0;
int main()
{
    
	for (i = 0;i <= 255;i++)
	{
    
		printf("hello world\n");
	}
	return 0;
}

答案

// char 有符号数 -128 ~ 127
// 无符号数 0 ~ 255
#include <stdio.h>
int main()
{
    
    char a = -1;
    //1000 0000 0000 0000 0000 0000 0001
    //1111 1111 1111 1111 1111 1111 1110
    //1111 1111 1111 1111 1111 1111 1111
    //截断
    //11111111 - a %d是有符号整型
    //整型提升
    //1111 1111 1111 1111 1111 1111 1111 1111 - 内存中的补码
    //1000 0000 0000 0000 0000 0000 0000 0000
    //1000 0000 0000 0000 0000 0000 0000 0001 -> -1

    signed char b = -1;
    unsigned char c = -1;
    //无符号数整型提升高位直接补 0
    printf("a=%d,b=%d,c=%d", a, b, c);
    return 0;
}

#include <stdio.h>
int main()
{
    
	char a = -128;
	//1000 0000 0000 0000 0000 0000 0100 0000
	//1111 1111 1111 1111 1111 1111 0111 1111
	//1111 1111 1111 1111 1111 1111 1000 0000 -截断
	//10000000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 - 提升
	//
	printf("%u\n", a);
	return 0;
}

#include <stdio.h>
int main()
{
    
	char a = 128;
	//0000 0000 0000 0000 0000 0000 1000 0000
	//0111 1111 1111 1111 1111 1111 0111 1111
	//0111 1111 1111 1111 1111 1111 1000 0000 - 截断
	//1000 0000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 - 提升
	printf("%u\n", a);
	//1000 0000 - a
	//1111 1111 1111 1111 1111 1111 1000 0000 - 提升
	//1000 0000 0000 0000 0000 0000 0111 1111
	//1000 0000 0000 0000 0000 0000 1000 0000
	printf("%d\n", a);
	return 0;
}

#include <stdio.h>
int main()
{
    
	int i = -20;
	// -20
	//1000 0000 0000 0000 0000 0000 0001 0100
	//1111 1111 1111 1111 1111 1111 1110 1011
	//1111 1111 1111 1111 1111 1111 1110 1100 -> -20的补码 

	unsigned int j = 10;
	//0000 0000 0000 0000 0000 0000 0000 1010
	printf("%d\n", i + j);
	//1111 1111 1111 1111 1111 1111 1110 1100
	//0000 0000 0000 0000 0000 0000 0001 1010
	//1111 1111 1111 1111 1111 1111 1111 0110
	// 
	//1000 0000 0000 0000 0000 0000 0000 1001
	//1000 0000 0000 0000 0000 0000 0000 1010
	return 0;
}

6.
7 .

#include <stdio.h>
unsigned char i = 0;
//unsigned char 类型取值范围 0~255 所以恒成立
int main()
{
    
	for (i = 0;i <= 255;i++)
	{
    
		printf("hello world\n");
	}
	return 0;
}


//死循环

重要

#include <stdio.h>
#include <string.h>
int main()
{
    
	if (strlen("abc") - strlen("abcdef") > 0)
	{
    
		//strlen 函数返回的类型是无符号整形，两个无符号整形详见得到的还是无符号整形
		printf(">\n");
		printf("%u\n", strlen("abc") - strlen("abcdef"));   //4294967293
	}
	else
	{
    
		printf("<\n");
	}
	return 0;
}


//如果想要算可以强制类型转换从整形或者比较大小

三、 浮点型在内存中的存储

常见的浮点数：
3.14159
1E10             1.0*pow(10,10)
浮点数家族包括：  float、double、long double 类型。
浮点数表示的范围： float.h中定义

他们被包含在这些头文件中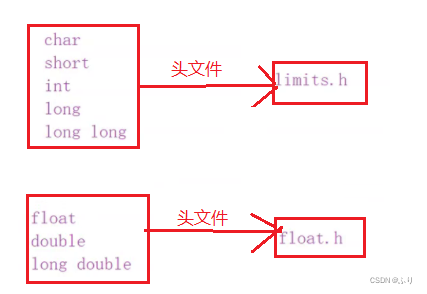

3.1 一个例子

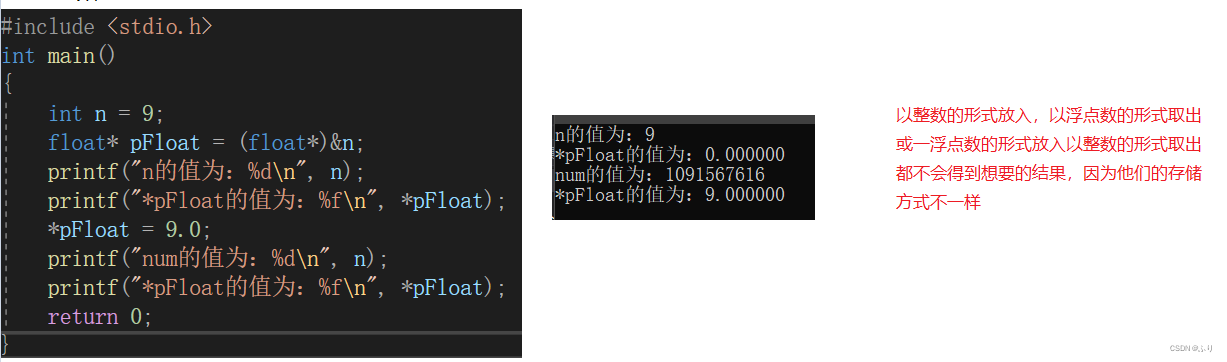
#include <stdio.h>
int main()
{
    
	int n = 9;
	float* pFloat = (float*)&n;
	printf("n的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	*pFloat = 9.0;
	printf("num的值为：%d\n", n);
	printf("*pFloat的值为：%f\n", *pFloat);
	return 0;
}

3.2 浮点数存储规则

num 和 *pFloat 在内存中明明是同一个数，为什么浮点数和整数的解读结果会差别这么大？

要理解这个结果，一定要搞懂浮点数在计算机内部的表示方法。

详细解读：

根据国际标准IEEE（电气和电子工程协会） 754，任意一个二进制浮点数V可以表示成下面的形式：

1. (-1)^S * M * 2^E
2. (-1)^s表示符号位，当s=0，V为正数；当s=1，V为负数。
3. M表示有效数字，大于等于1，小于2。
4. 2^E表示指数位。

举例来说 ：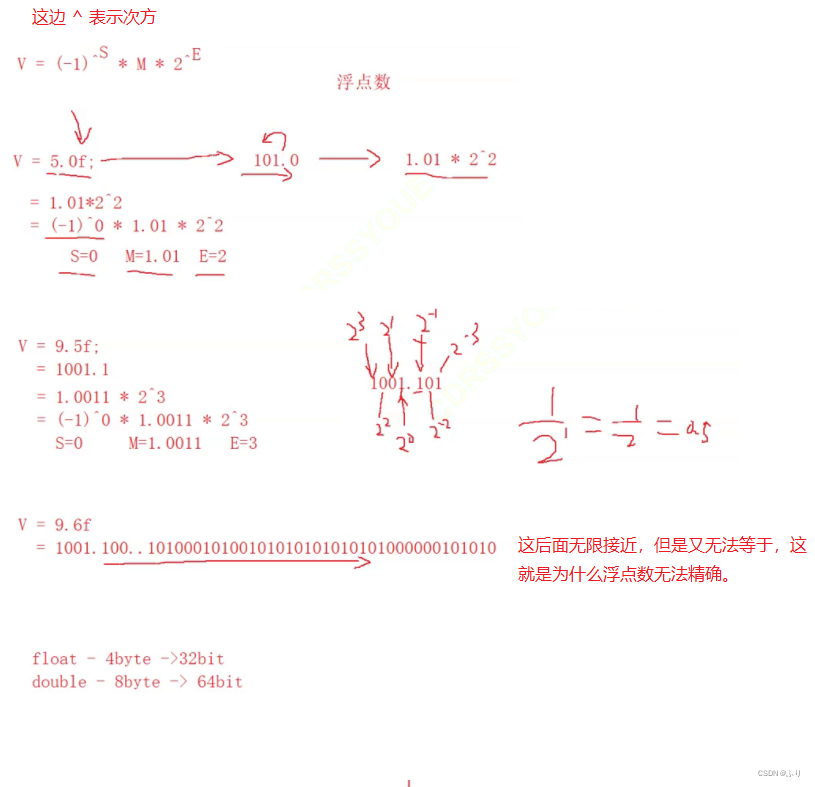

首先，E为一个无符号整数（unsigned int）

1. 这意味着，如果E为8位，它的取值范围为0 ~ 255；
2. 如果E为11位，它的取值范围为0~2047。
3. 但是，我们知道，科学计数法中的E是可以出现负数的，所以IEEE754规定：

存入内存时E的真实值必须再加上一个中间数，
对于8位的E，这个中间数是127；
对于11位的E，这个中间数是1023。

比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001。

指数E从内存中取出还可以再分成三种情况：

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将
有效数字M前加上第一位的1。
比如：
0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到2300000000000000000000000，则其二进制表示形式为:

0 01111110 00000000000000000000000

E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于
0的很小的数字。

E全为1

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

解释前面的题目：

为什么 0x00000009 还原成浮点数，就成了 0.000000 ？

首先，将 0x00000009 拆分，得到第一位符号位s=0，后面8位的指数 E=00000000 ，最后23位的有效数字M=000 0000 0000 0000 0000 1001。

9 -> 0000 0000 0000 0000 0000 0000 0000 1001

由于指数E全为0，所以符合上一节的第二种情况。因此，浮点数V就写成：

显然，V是一个很小的接近于0的正数，所以用十进制小数表示就是0.000000。

再看例题的第二部分。

请问浮点数9.0，如何用二进制表示？还原成十进制又是多少？

9.0 -> 1001.0 ->(-1)^01.00123 -> s=0, M=1.001,E=3+127=130

首先，浮点数9.0等于二进制的1001.0，即1.001×2^3。

那么，第一位的符号位s=0，有效数字M等于001后面再加20个0，凑满23位，指数E等3+127=130， 即10000010。

所以，写成二进制形式，应该是s+E+M，即

0 10000010 001 0000 0000 0000 0000 0000

这个32位的二进制数，还原成十进制，正是 1091567616 。