当前位置:网站首页>【机器学习 03】拉格朗日乘子法
【机器学习 03】拉格朗日乘子法
2022-07-07 08:30:00 【ECCUSXR】
目录
1 与原点的最短距离

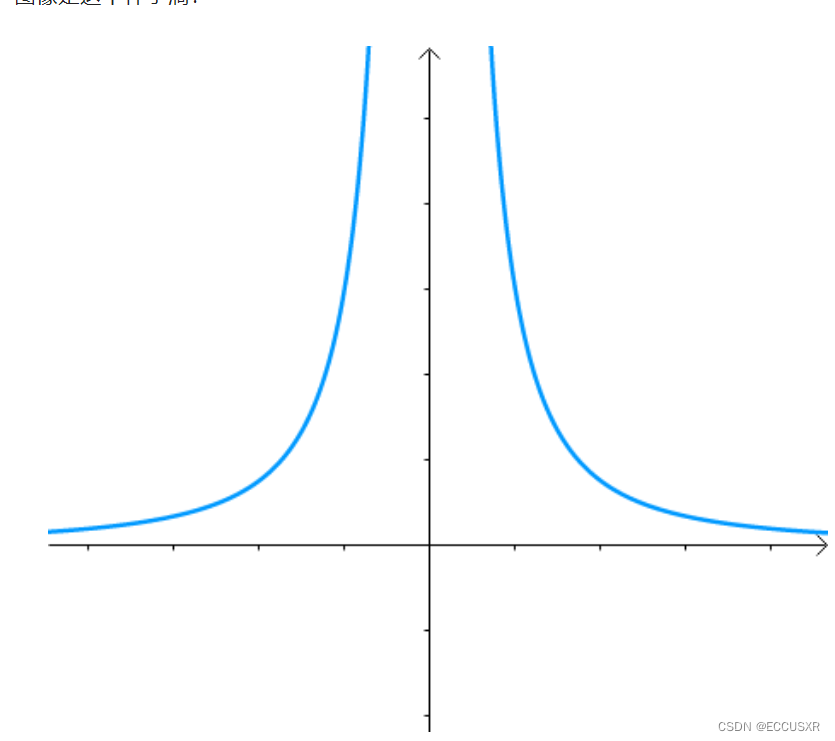 现在我们想求其上的点与原点的最短距离:
现在我们想求其上的点与原点的最短距离:
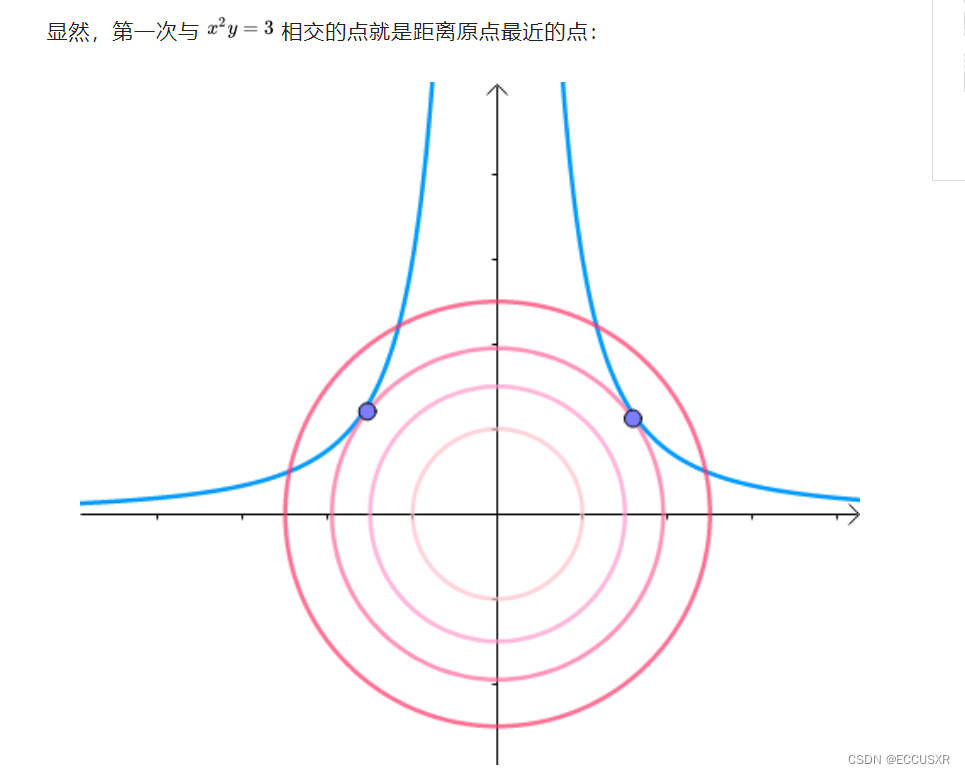
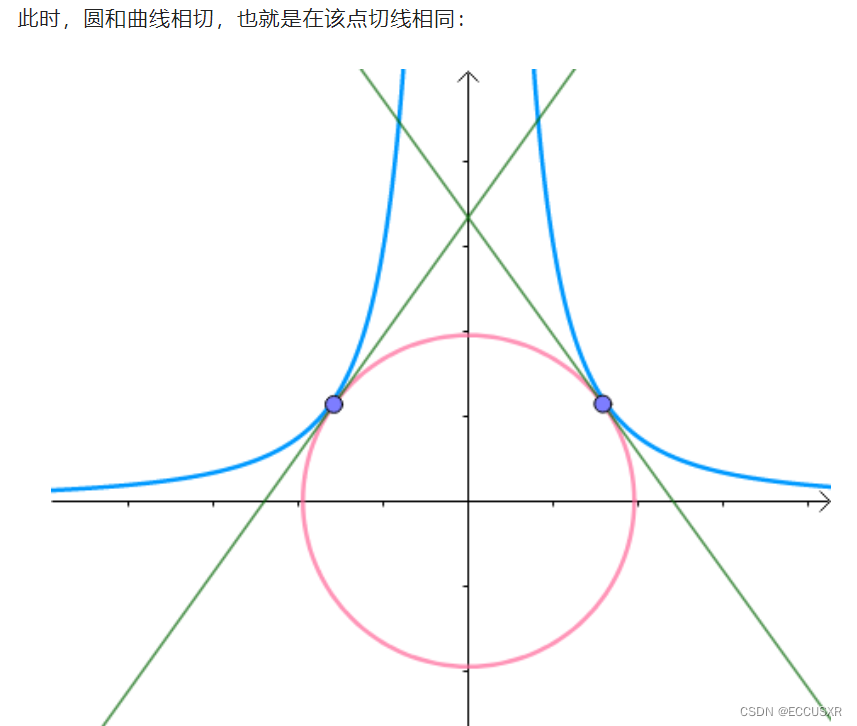
2 等高线
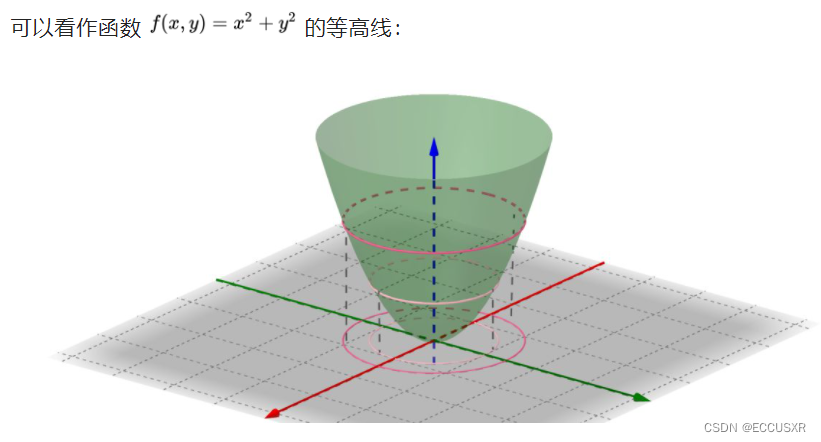
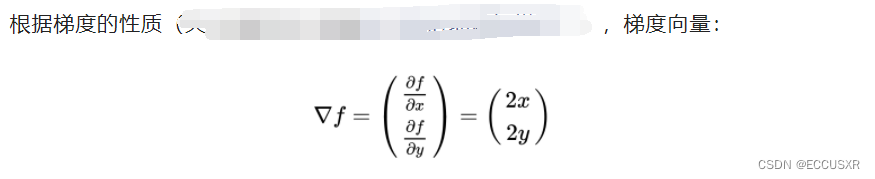
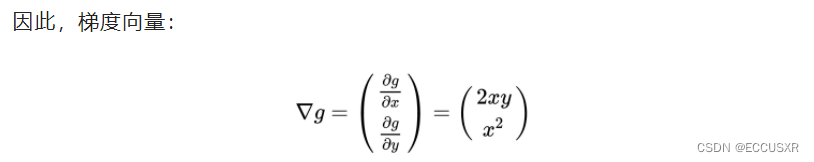
3 拉格朗日乘子法

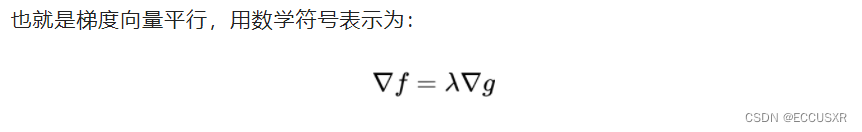
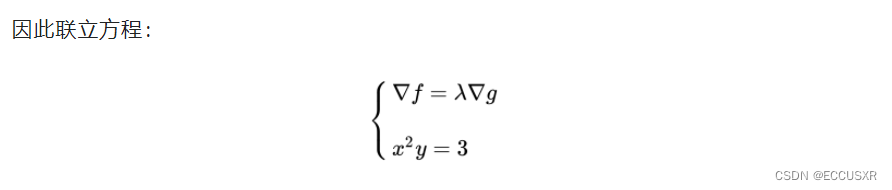
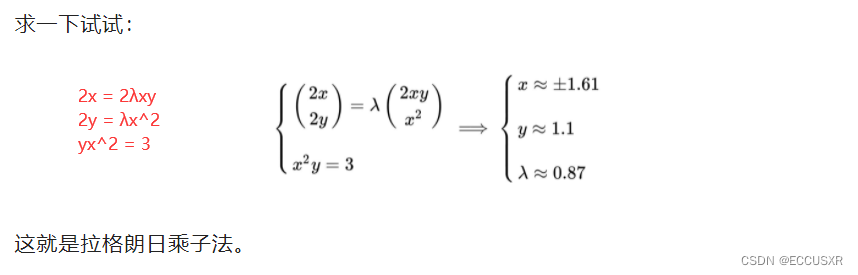 4 拉格朗日乘子法 定义
4 拉格朗日乘子法 定义



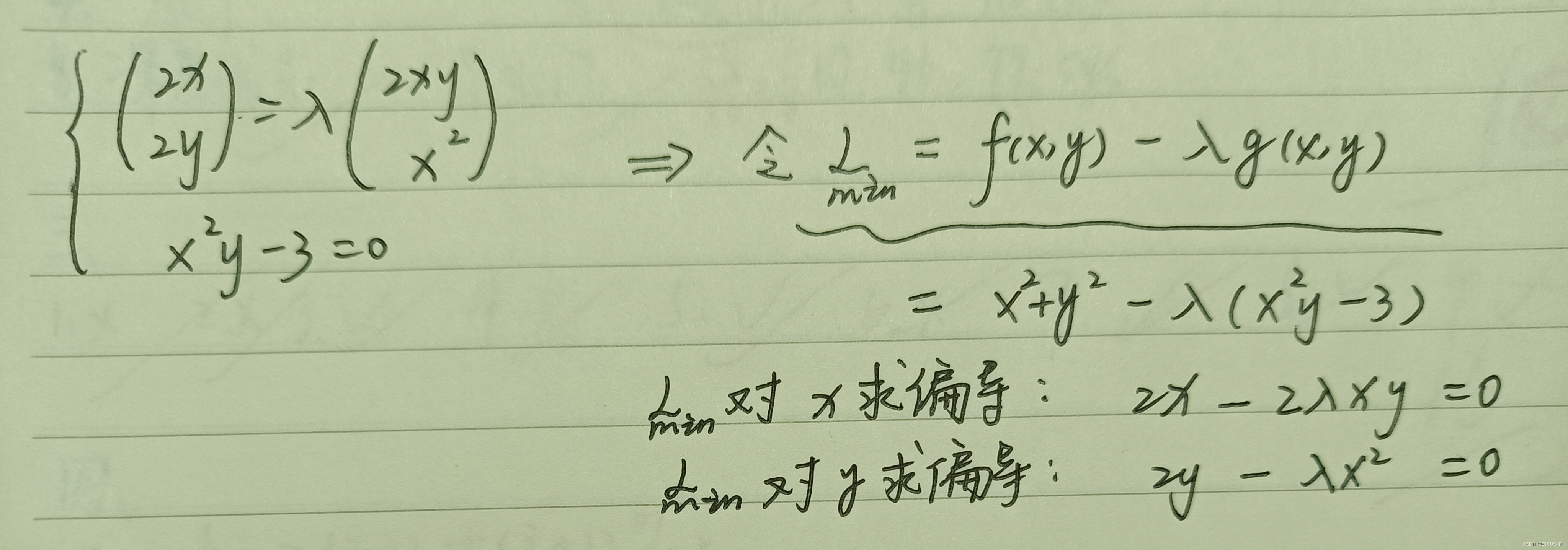
5 多个约束条件



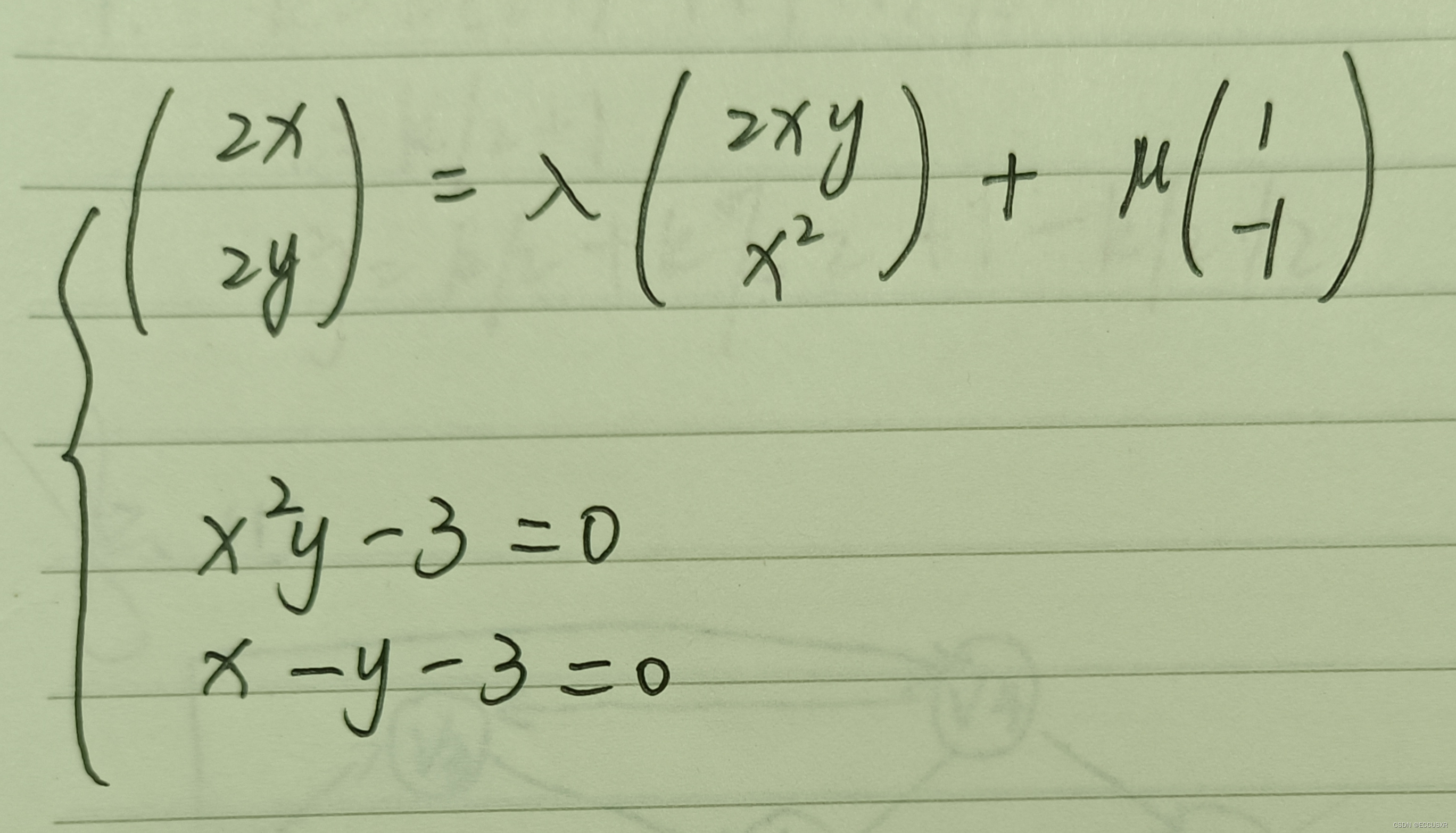
4 不等式约束下的极值
直接看第二个链接
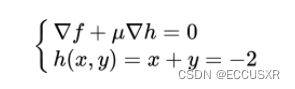
链接中 4.3 新增的条件 讲述 为什么在不等式约束下,上面第一个式子等于0。
目标函数和梯度下降函数的方向相反。
5 KTT条件

边栏推荐
- Summary of router development knowledge
- 字符串格式化
- Leetcode-304: two dimensional area and retrieval - matrix immutable
- table宽度比tbody宽度大4px
- Why is the reflection efficiency low?
- I'd rather say simple problems a hundred times than do complex problems once
- [higherhrnet] higherhrnet detailed heat map regression code of higherhrnet
- Prototype and prototype chain
- Multisim--软件相关使用技巧
- ThreadLocal会用可不够
猜你喜欢
随机推荐
Experience sharing of software designers preparing for exams
IIC基本知识
leetcode-560:和为 K 的子数组
IO模型复习
ArrayList线程不安全和解决方案
Summary of router development knowledge
求最大公约数与最小公倍数(C语言)
Basic introduction of yarn and job submission process
电表远程抄表拉合闸操作命令指令
BigDecimal数值比较
2022.7.6DAY598
中级软件评测师考什么
BigDecimal value comparison
Application of OpenGL gllightfv function and related knowledge of light source
【华为机试真题详解】高矮个子排队
【二开】【JeecgBoot】修改分页参数
嵌入式工程师如何提高工作效率
Multisim -- software related skills
Multisim--软件相关使用技巧
深入分析ERC-4907协议的主要内容,思考此协议对NFT市场流动性意义!

![1323: [example 6.5] activity selection](/img/2e/ba74f1c56b8a180399e5d3172c7b6d.png)