当前位置:网站首页>[paper reading | deep reading] dngr:deep neural networks for learning graph representations
[paper reading | deep reading] dngr:deep neural networks for learning graph representations
2022-07-07 02:18:00 【Haihong Pro】
Catalog

Preface
Hello!
Thank you very much for reading Haihong's article , If there are mistakes in the text , You are welcome to point out ~
Self introduction. ଘ(੭ˊᵕˋ)੭
nickname : Sea boom
label : Program the ape |C++ player | Student
brief introduction : because C Language and programming , Then I turned to computer science , Won a National Scholarship , I was lucky to win some national awards in the competition 、 Provincial award … It has been insured .
Learning experience : Solid foundation + Take more notes + Knock more code + Think more + Learn English well !
Only hard work
Know what it is Know why !
This article only records what you are interested in
brief introduction
Link to the original text :https://dl.acm.org/doi/abs/10.5555/3015812.3015982
meeting :AAAI‘16 (CCF A class )
year :2016
Abstract
In this paper , We propose a new model of learning graph representation
The model captures Figure structure information To generate a low dimensional vector representation of each vertex
Different from previous studies , We use Random surfing model ( random surfing model) Get the structure information of the graph directly , Instead of using Perozzi wait forsomeone (2014) The proposed sampling based method generates linear sequences
We also Levy and Goldberg(2014) The proposed matrix decomposition method provides a new perspective :
- In this method , Pointwise mutual information (pointwise mutual information,PMI) Matrices are considered Mikolov The analytical solution of the objective function of the jump graph model with negative sampling proposed by et al
- Their approach involves using SVD from PMI Find low dimensional projection in matrix
It probably means to use PMI Matrix can achieve the effect similar to the jump graph model ( Use matrices instead of Neural Networks )
However , The difference is , In our model Stack denoising self encoder To extract complex features and model nonlinearity
1 Introduction
In many practical problems , Graphics is a common form of information management
for example , In the study of protein networks
From protein - Mining protein complexes in protein interaction networks plays an important role in describing the functional diversity of homologous proteins and valuable evolutionary insights , This is essentially a clustering problem
It is crucial to develop automatic algorithms to extract useful depth information from charts
One of the effective ways to organize this information related to potentially large complex graphs is to learn graph representation
It assigns a low dimensional dense vector representation to each vertex of the graph , The meaningful information conveyed by the coding diagram
lately , People have a strong interest in learning vocabulary embedding (Bullinaria and Levy 2007;Mikolov wait forsomeone 2013)
Their goal is to learn the low dimensional vector representation of each context based natural language word from a large number of natural language texts
These works can be regarded as learning representations of linear sequences , Because the corpus is composed of linear structure , Linear structure is a natural language word sequence
The resulting compactness 、 Low dimensional vector representation is considered to be able to capture rich semantic information , It has been proved to be useful for various naturallanguageprocessing tasks
Although efficient and effective methods for learning good representations of linear structures have been identified (Mikolov et al. 2013;Pennington, Socher and Manning 2014), It is more complicated to deal with general graph structures with rich topological structures
So , A natural way is to identify effective methods , The task of learning the vertex representation of general graph structure is transformed into the task of learning the representation from linear structure
Perozzi wait forsomeone (2014) Proposed DeepWalk Put forward an idea , Through a uniform sampling method called truncated random walk , Convert the unweighted graph into a set of linear sequences
- In their approach , The sampled vertex sequence represents the connection between vertices in the graph , This step can be understood as the process of transforming the general graph structure into a large set of linear structures
- Next , They use Mikolov wait forsomeone (2013) Proposed Jump Graph Model (skip-gram model) Learn the low dimensional representation of vertices from this linear structure
- The learned vertex representation has been proved to be effective in some tasks , Better than previous methods , Such as spectral clustering and modular methods (Tang and Liu 2009a;2009 b;2011;2003 Year of Macskassy and Provost).
Although this method of learning unweighted graph vertex representation is effective , But there are still two important questions to be answered
- 1) First , How to be more accurate 、 Get the graph structure information of weighted graph more directly ?
- 2) second , Is there a better way to represent the vertices of linear structure ?
To answer the first question
- We design a random surfing model suitable for weighted graphs , It can directly generate a probability co-occurrence matrix
- Such a matrix is similar to the concurrency matrix obtained by sampling a linear sequence from a graph (Bullinaria and Levy 2007), But our method does not need the sampling process
To answer the second question
- We first review a popular method for learning vertex representations of linear structures
- Levy and Goldberg(2014) A recent study shows that , Using the negative sampling method to optimize the objective function related to the Jump Graph (Mikolov wait forsomeone 2013) And decomposing words and The shift of its context punctually mutual information (PPMI) matrix There's an inner connection
- say concretely , They showed Use standard singular value decomposition (SVD) Method pair PPMI Matrix decomposition , Thus, the vertex can be induced from the decomposed matrix / Word representation is possible
Recent methods :GraRep (Cao, Lu, and Xu 2015), It has been proved that good empirical results have been achieved in the task represented by learning graph
However , This method adopts singular value decomposition (SVD) Linear dimensionality reduction , No better nonlinear dimensionality reduction technology has been explored
In this paper , We give Levy and Goldberg(2014) Our work provides a new perspective
We think primitive PPMI Matrix itself is the explicit representation matrix of graph ,SVD Steps essentially act as a dimension reduction toolbox
although SVD Step induced final word representation proved to be effective ,Levy wait forsomeone (2015) It also proves that the use of PPMI The validity of the matrix itself as a word representation
Interestingly , As the author shows , from SVD The representation learned by the method cannot completely exceed PPMI The representation of the matrix itself (Levy, Goldberg, and Dagan 2015)
Because our ultimate goal is to learn good vertex representation , Effectively capture the information of the graph
Research from PPMI A better way to restore vertex representation in a matrix is crucial , Here you can capture the potential complexity between different vertices 、 Nonlinear relation
Deep learning illuminates the path of modeling nonlinear complex phenomena , There are many successful applications in different fields , Such as speech recognition (Dahl et al. 2012) And computer vision
Deep neural network (DNN), For example, self encoder is an effective method to learn high-level abstractions from low-level features
This process essentially performs dimensionality reduction , Map data from high dimensional space to low dimensional space
And based on ( truncation )svd Dimension reduction method of ( From the original representation space to a new low rank space by linear projection ) Different , Deep neural network ( Such as stacking self encoder ) Can learn highly nonlinear projection
in fact ,Tian et al.(2014) A recent work used a sparse self encoder to replace the eigenvalue decomposition step of spectral clustering in clustering tasks , Significant improvements have been made
Inspired by their work , We also studied the effectiveness of using an alternative method based on deep learning to learn low dimensional representations from raw data representations
Different from their work , Our goal is to learn the vertex representation of general graphs , Instead of focusing on clustering tasks .
We apply the deep learning method to PPMI matrix , Not the Laplace matrix used in their model
The former has been shown to have the potential to produce better performance than the latter
In order to enhance the robustness of our model , We also use stack de-noising self encoder to learn multi-layer representation
We call our proposed model DNGR( Deep neural network for graph representation )
The learned representation can be regarded as an input feature , It can be input into other tasks , Such as unsupervised clustering and supervised classification tasks
To verify the effectiveness of our model , We did experiments , Apply the learned representation to a series of different tasks , It considers different types and topologies of networks in the real world
In order to further prove that our model is considering simpler 、 Effectiveness of larger scale actual graph structure , We apply our algorithm to a very large language data set , The experiment was carried out on the task of word similarity
In all of these missions , Our model is superior to other methods in learning graph representation , And our model can also be parallelized
Our main contribution has two aspects :
- In theory , We believe that the advantage of deep neural network is that it can capture the nonlinear information conveyed by the graph , The traditional linear dimensionality reduction method can not easily capture these information . Besides , We believe that our random surfing model can be used to replace the widely used traditional sampling based method to collect chart information .
- Empirically , We prove that our new model can better learn the low dimensional vertex representation of weighted graphs , Among them, meaningful semantics , Diagrams of relationship and structural information can be captured . We show that the result representation can be effectively used as a feature for different downstream tasks .
2 Background and Related Work
In this section , We
- First of all, it shows an example in DeepWalk Random sampling of weighted graph proposed in , To illustrate the feasibility of converting vertex representation to linear representation
- Next , We consider two ways of expressing words : Jump Graph with negative sampling and based on PPMI Matrix decomposition of matrix . These methods can be regarded as linear methods for learning lexical representation from linear structure data .
Notation
G = ( V , E ) G = (V, E) G=(V,E)
V V V: Vertex set
E E E: Edge set
In an unweighted graph , Edge weight indicates whether there is a relationship between two vertices , So it is Binary relation
contrary , The edge weight in a weighted graph is a real number that represents the degree of association between two vertices . Although the edge weight in the weighted graph can be negative , But this article only considers non negative weight
For marking purposes , We also use w w w and c c c To represent the vertex
We try to capture depth structure information to obtain a representation G G G Vertex matrix R R R(R That is, we need to find the embedding )
2.1 Random Walk in DeepWalk
DeepWalk It provides an effective method to truncate random walk , The unweighted graph structure information is transformed into a linear sequence representing the relationship between graph vertices
The proposed random walk is a uniform sampling method , For non weighted graphs
- They first randomly select a vertex from the graph v 1 v_1 v1, And mark it as the current vertex
- Then from the current vertex v 1 v_1 v1 Randomly select the next vertex from all neighbors of v 2 v_2 v2
- Now? , They put this newly selected vertex v 2 v_2 v2 Mark as current vertex , And repeat the vertex sampling process
- When the number of vertices in a sequence reaches a preset value , That is, the walking length η η η when , Algorithm was terminated
- Repeat the process γ γ γ Time ( It is called total walking ) after , Collect linear sequence blocks
Truncated random walk is an effective method to express the structure information of unweighted graphs by using linear sequences , But it's The sampling process is slow , And super parameter η η η and γ γ γ Not easy to determine
We noticed that ,DeepWalk A co-occurrence matrix based on sampled linear sequence is generated .
Briefly introduce DeepWalk
In the third section , We described our Random surfing model , The model constructs a probability co-occurrence matrix directly from a weighted graph , Thus, the expensive sampling process is avoided
2.2 Skip-gram with Negative Sampling
The natural language corpus is composed of a linear sequence of word streams
In recent years , Neural embedding method and matrix decomposition based method have been widely used in vocabulary representation learning .
stay (Mikolov et al. 2013) The jump graph model proposed in has been proved to be an effective and efficient method for learning word representation
Two noteworthy ways to improve the jump graph model are
- Negative sampling (SGNS)
- layered softmax
In this paper , We choose to use the former method : Negative sampling (SGNS)
stay SGNS in , Noise comparison estimate (NCE) A simplified variant of the method (Gutmann and Hyv̈arinen 2012; use Mnih and Teh 2012) To enhance the robustness of the jump graph model
SGNS Randomly create negative pairs from the empirical distribution of single letter words ( w , c N ) (w, c_N) (w,cN), And try to use a low dimensional vector to represent each word w ∈ V w∈V w∈V And context words c ∈ V c∈V c∈V Yes
SGNS The objective function of is to align ( w , c ) (w, c) (w,c) Maximum , Negative pair ( w , c N ) (w, c_N) (w,cN) Minimum
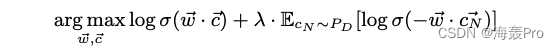
In style
- σ ( ⋅ ) σ(·) σ(⋅) by σ ( x ) = ( 1 + e − x ) − 1 σ(x) = (1 +e^{−x})^{−1} σ(x)=(1+e−x)−1 Of sigmoid function
- λ λ λ Is the number of negative samples . E c N ∼ p D [ ⋅ ] E_{c_N \sim p_D}[·] EcN∼pD[⋅] Is negative sampling c N c_N cN The example obtained conforms to the distribution p D = # ( c ) ∣ D ∣ pD = \frac{\#(c)}{|D|} pD=∣D∣#(c) ( singular c In the data set D Distribution in ) The expectation of the time
Introduce Skip-gram Model ( Using negative sampling )
2.3 PMI matrix and SVD
Learn graphic representation ( Especially word expression ) Another way of doing this is Based on matrix factorization Technology
These methods are based on Statistics of global co-occurrence count to learn the representation , And in some prediction tasks, it can be better than the neural network method based on a single local context window
An example of a matrix factorization method is Hyperspace analogical analysis (Lund And Burgess 1996),
- It factorizes words - Word co-occurrence matrix is represented by production words
- The main disadvantages of this method and related methods are : Frequent words with relatively few semantic values ( for example , Stop words ) It has a disproportionate impact on the generated word representation
Church and Hanks Point by point mutual information (PMI) matrix It is to solve this problem that , It was later proved Provides better word representation
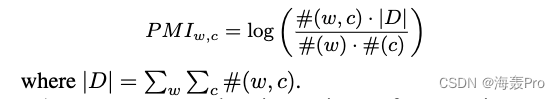
A common way to improve performance is Assign each negative value to 0, This is in (Levy and Goldberg 2014) It's detailed in , With formation PPMI matrix
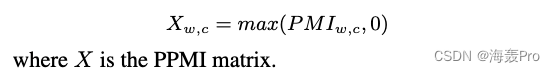
PMI matrix → \rightarrow → PPMI matrix
although PPMI Matrix is a high-dimensional matrix , But use Truncated singular value decomposition method Dimensionality reduction will produce information about L 2 L_2 L2 Optimal rank factorization of loss
Let's assume the matrix X X X It can be decomposed into three matrices U Σ V T UΣV^T UΣVT
- U U U and V V V It's an orthogonal matrix
- Σ Σ Σ It's diagonal
let me put it another way :
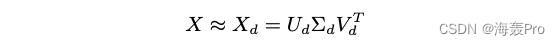
here
- U d U_d Ud and V d V_d Vd Is corresponding to the former d d d Singular values ( stay Σ d Σ_d Σd in ) Of U U U and V V V The left side of the d d d Column
according to Levy And so on .(2015), Word representation matrix R R R It can be :

PPMI matrix X X X yes The word represents the product of the matrix and the context matrix
Singular value decomposition (SVD) The process provides a way from matrix X X X Find matrix in R R R Methods , among
- R R R The line vector of is a word / Low dimensional representation of vertices , Can pass X X X Given the linear projection of the high-dimensional representation
We believe that such a projection is not necessarily a linear projection
In this work , We study the use of nonlinear projection method instead of linear singular value decomposition method by using deep neural network
2.4 Deep Neural Networks
Deep neural network can be used to learn multi-level feature representation , It has achieved successful results in different fields
Training such networks has proved difficult , An effective solution , stay (Hinton and Salakhutdinov,2006;Bengio et al.2007), It uses greedy hierarchical unsupervised pre training
This strategy aims to learn useful representations of each layer at once , It aims to learn useful representations of each layer at once
then , Feed the learned low-level representation to the next layer as input , Used for subsequent expression learning
Neural networks usually use such as Sigmoid or tanh Such nonlinear activation functions to capture the complex from input to output 、 Nonlinear projection
In order to train the deep architecture involving multi-layer feature representation , Automatic encoder has become one of the commonly used building blocks. Automatic encoder performs two actions – Coding steps , Then there is the decoding step .
A little (AE For the time being )
Stackable automatic coder is a multilayer deep neural network composed of multilayer automatic coders
Stackable automatic encoder uses layer by layer training method to extract basic rules , These rules capture different levels of abstraction from the data layer by layer , The higher level conveys a higher level of abstraction from the data
3 DNGR Model
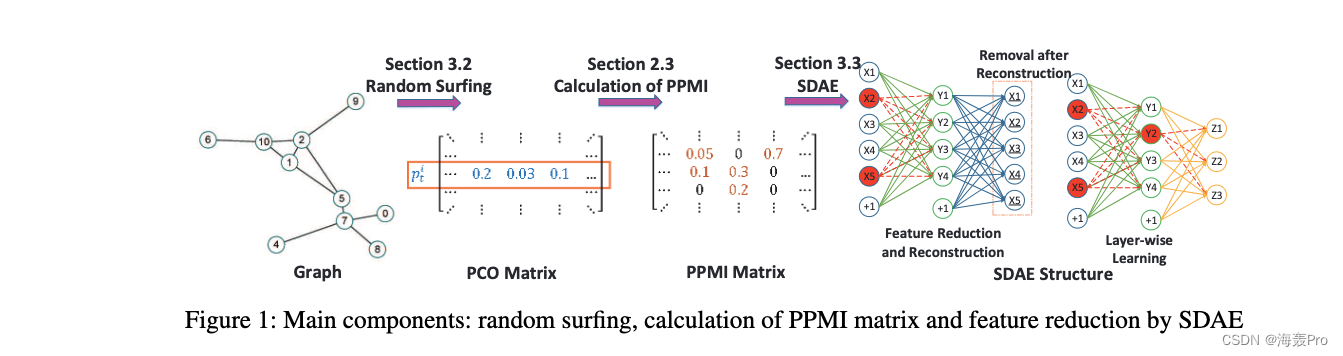
Pictured 1 Shown , The model consists of three main steps
- First , Random surfing model is introduced to capture graph structure information , And generate a Probability co-occurrence matrix
- Next , We calculate according to the probability co-occurrence matrix PPMI matrix ( See the first 2.3 section )
- after , A stacked denoising self encoder ( The first 3.2 section ) Used to learn low dimensional vertex representation
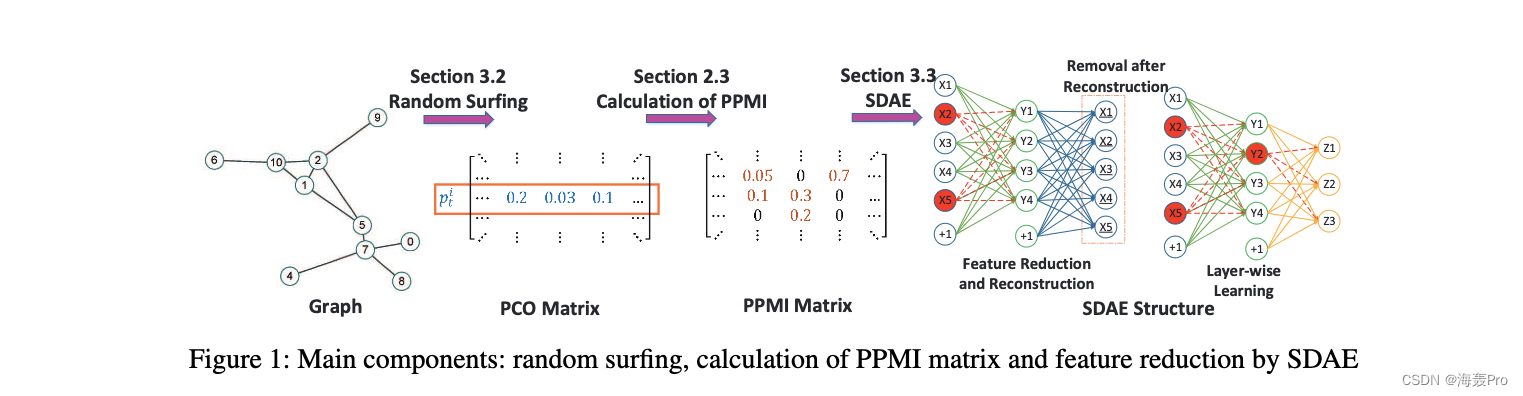
3.1 Random Surfing and Context Weighting
Although the sampling method of converting graph structure into linear sequence is effective , But there are also some disadvantages :
- First , The sampling sequence has a finite length . This makes it difficult for the vertices appearing at the boundary of the sampling sequence to obtain the correct context information
- secondly , Determine some super parameters, such as step size η η η And total step size γ γ γ Not simple , Especially for large graphs
To solve these problems , We consider using a Random surfing model
The model is used for task ranking PageRank Model inspired
Let's start with a diagram Randomly arrange vertices
Suppose the current vertex is i i i vertices , There is a transformation matrix A A A To catch Transition probability between different vertices
We introduce a row vector p k p_k pk
- It's the first j j j Elements represent the process k k k After the step transition, you reach the j j j Probability of vertices
- p 0 p_0 p0 It's No i i i The value of each element is 1, All the other elements are 0 Initial 1-hot vector
Let's consider a There is a restart Random surfing model :
- At every point in time , There is a random surfing process continue Probability α α α
- There is a probability that the random surfing process will return to the original vertex and restart 1 − α 1−α 1−α
This leads to the following recursive relationship :
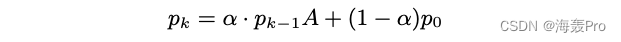
If we assume that there is no random restart in this process , Then it happened k k k The probability of reaching different vertices after step conversion is as follows :
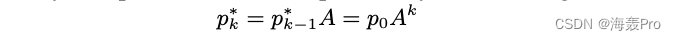
It's the same time α = 1 \alpha = 1 α=1
Intuitively speaking , The closer the distance between the two vertices , The closer the relationship between them should be
therefore , It is reasonable to measure its importance according to the relative distance between the context node and the current node
This weighting strategy is used in word2vec and GloVe Have been implemented , And found to be important for achieving good empirical results
Based on this fact , We can see , Ideally , The first i i i The representation of vertices should be constructed in the following way :
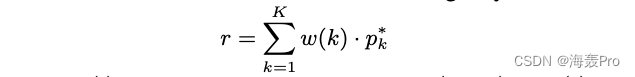
- W ( ⋅ ) W(·) W(⋅) Is a decreasing function , namely W ( t + 1 ) < W ( t ) W (t + 1) < W (t) W(t+1)<W(t)
Ideally
We think , The following vertex representation construction method based on the above random surfing process actually meets the above conditions :
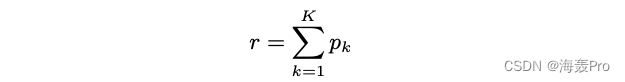
The actual situation
In fact, it can be proved that we have the following points :
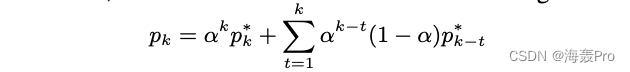
among p 0 ∗ = p 0 p^∗_0 = p_0 p0∗=p0, p t ∗ p^*_t pt∗ stay r r r The coefficient in is
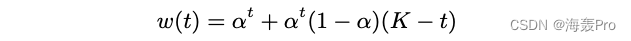
- w ( t ) w(t) w(t) yes α < 1 α < 1 α<1 The decreasing function of
The weight function in the jump graph can be described as
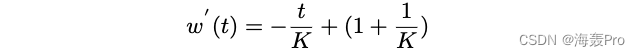
GloVe The weight function in is :
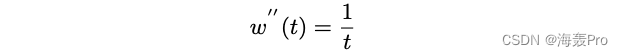
From the picture 2 It can be seen that , All weight functions are monotonically decreasing functions 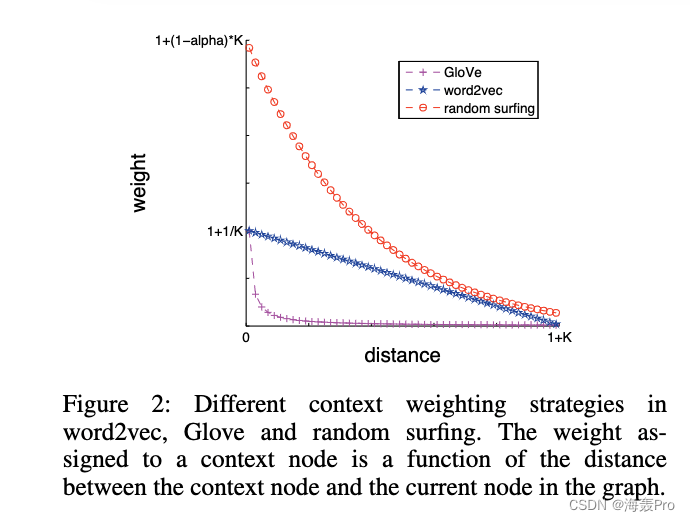
And word2vec and GloVe similar , Our model also allows different weighting according to the distance from the context information to the target
This has previously proved important for building good word representation
3.2 Stacked Denoising Autoencoder
We aim to study from PPMI Construct high-quality low dimensional vector representation in the matrix , To convey the basic structural information of the diagram
SVD( Singular value decomposition ) Although the process is effective , But in essence, it only produces from PPMI The linear transformation from the vector representation contained in the matrix to the final low dimensional vertex vector representation
We believe that a potential nonlinear mapping can be established between these two vector spaces
therefore , We use stack denoising self encoder ( A model commonly used in deep learning ), Generate compressed low dimensional vectors from the original high-dimensional vertex vectors
As shown in the table 1 Shown , We first initialize the parameters of the neural network , Then the greedy hierarchical training strategy is used to learn the high-level abstraction of each layer 
To enhance DNN The robustness of , We use stack denoising self encoder (SDAE)
Different from the traditional automatic encoder , Before the training steps , The denoising automatic encoder will Partially destroy the input data
- To be specific , We randomly destroy each input sample x x x( A vector ), With a certain probability, some entries in the vector are assigned 0
This idea is similar to modeling missing items in a matrix completion task , The goal is to use the regularity in the data matrix , Effectively recover the complete matrix under specific assumptions
In the picture 1 Shown SDAE In structure
- X i X_i Xi Corresponding input data
- Y i Y_i Yi Corresponding to the representation learned in the first layer
- Z i Z_i Zi Corresponding to the representation learned in the second layer
- Temporarily damaged nodes ( Such as X 2 、 X 5 and Y 2 X_2、X_5 and Y_2 X2、X5 and Y2) Highlight... In red
Similar to standard automatic encoder , Once again, we reconstruct data from potential representations . let me put it another way , We are interested in :
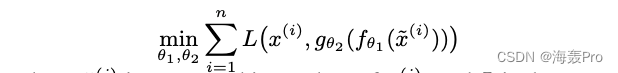
among
- x ~ ( i ) \widetilde x^{(i)} x(i) Is corrupted input data x ( i ) x^{(i)} x(i)
- L L L Is the standard square loss
3.3 Discussions of the DNGR Model
Let's analyze DNGR The advantages of
- Random Surfing Strategy: As we are above 3.1 Section , The random surfing process overcomes the limitations associated with the sampling process used in previous work , It's for us Provides some desired properties , These properties are shared by implementations of previously embedded models , Such as word2vec and GloVe.
- Stacking Strategy: The stacking structure provides A smooth way to reduce dimension . We believe that , The representations learned at different levels of the deep architecture can provide different levels of meaningful abstraction for the input data .
- Denoising Strategy: High dimensional input data often contain redundant information and noise . It is considered that the denoising strategy can Effectively reduce noise , Robustness enhancement
- Efficiency: Based on the previous analysis (Tian et al. 2014), In terms of the number of vertices in the graph ,DNGR The self encoder inference ratio used in is based on svd The matrix decomposition method of With lower time complexity .SVD The time complexity of is at least the quadratic element of the vertex number . However ,DNGR The reasoning time complexity of is linear in the number of vertices in the graph
4 Datasets, Baselines
4.1 Datasets
- 20-NewsGroup
- Wine
- Wikipedia Corpus
4.2 Baseline Algorithms
- DeepWalk
- SGNS
- PPMI
- SVD
5 Experiments
5.1 Parameters

5.2 Experiments
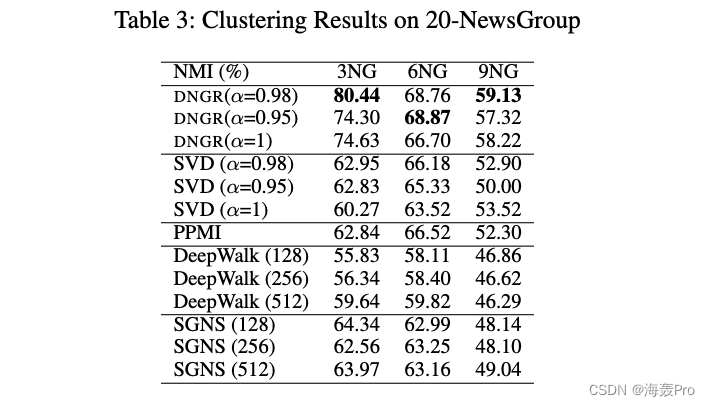
5.2.1 Clustering Task on the 20-NewsGroup Network
5.2.2 Visualization of Wine

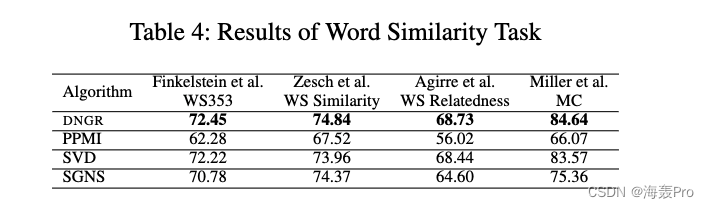
5.2.3 Word Similarity Task
5.2.4 Importance of Deep Structures
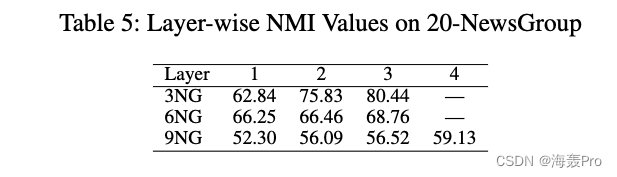
In order to understand the necessity of depth structure , We further measured 20-NewsGroup Layer by layer of NMI value . about 3NG and 6NG, We use 3 Layer neural network to construct representation , about 9NG, We use 4 layer , As shown in the table 2 Shown . From the table 5 It can be seen that , On the whole, the performance of the three networks has been improved from shallow to deep , This shows the importance of deep structure .
6 Conclusion
In this paper , We propose a depth map representation model , Each vertex is encoded into a low dimensional vector representation
Our model shows the ability of stack de-noising automatic encoder to extract meaningful information and generate information representation
We carried out experiments on real data sets of different tasks , It turns out that , The performance of this model is better than several most advanced baseline algorithms
Although the process of adjusting the superparameters of neural networks requires effort and expertise , But our conclusion is , Exploring the underlying structure of data through deep learning can improve the representation of graphs
After reading the summary
After reading this article, I don't feel that I understand it deeply
Because there is little in-depth understanding of using matrix decomposition to solve embedding , about PPMI Not familiar with matrix
The whole article adopts the random surfing model + PPMI + SNAE combination
- First, we use the random surfing model to get a Probability co-occurrence matrix
- recycling Probability co-occurrence matrix generating PPMI matrix
- Reuse PPMI Matrix uses SNAE Learn its low dimensional representation
One of the difficulties : Random surfing model
Personal understanding , It probably means that you can get effects like Jump Graph Model , Not using random walk , Instead, it uses a probability transfer , Generate the probability transfer matrix between vertices , Then we can use this matrix , obtain , such as , Find the context of a node ( It will be very convenient , Direct calculation with the help of mathematical formulas , No longer need to use neural networks )
Difficulty 2 :PPMI matrix
With the help of Probability co-occurrence matrix , You can calculate PMI matrix
Specifically, how to transform , I didn't understand (emmm, I really don't understand , Good food )
Then I'm right PMI Negative values in the matrix are converted to 0, So you get PPMI matrix
The third difficulty : Use SNAE Learning to embed
about PPMI matrix X X X, Use x i x_i xi As SNAE The input of
Through the iteration of multiple hidden layer neural networks , Get the low dimensional vector , And then decode it
Optimize parameters by reconstructing losses
Because the previous method gets PPMI After matrix , Reuse SVD( Singular value decomposition ) Get low dimensional embedding
The explanation can be through PPMI Get low dimensional embedding
Here the author uses SNAE To get this low dimensional embedding
I have a little understanding of the idea
There are still many details that I don't understand
If there is anything you need to know in detail later , Read more carefully !
Conclusion
The article is only used as a personal study note , Record from 0 To 1 A process of
Hope to help you a little bit , If you have any mistakes, you are welcome to correct them

边栏推荐
- Dall-E Mini的Mega版本模型发布,已开放下载
- Flir Blackfly S 工业相机:自动曝光配置及代码
- ROS learning (26) dynamic parameter configuration
- The use of video in the wiper component causes full screen dislocation
- Modify the system time of Px4 flight control
- 开发中对集合里面的数据根据属性进行合并数量时犯的错误
- 将截断字符串或二进制数据
- Twenty or thirty thousand a leaf? "Yang Mou" behind the explosion of plant consumption
- 【论文阅读|深读】ANRL: Attributed Network Representation Learning via Deep Neural Networks
- Cisp-pte practice explanation (II)
猜你喜欢
A new path for enterprise mid Platform Construction -- low code platform
How did partydao turn a tweet into a $200million product Dao in one year
3D激光SLAM:Livox激光雷达硬件时间同步

STM32F4---PWM输出

建议收藏!!Flutter状态管理插件哪家强?请看岛上码农的排行榜!
ROS學習(23)action通信機制
TiFlash 源码阅读(四)TiFlash DDL 模块设计及实现分析

Stm32f4 --- PWM output
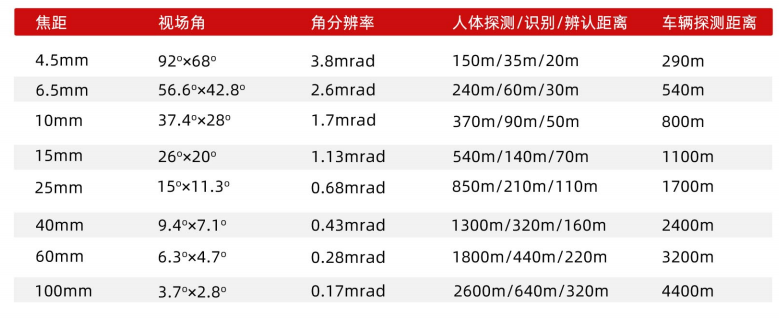
Infrared camera: juge infrared mag32 product introduction

go swagger使用
随机推荐
Zabbix 5.0:通过LLD方式自动化监控阿里云RDS
张平安:加快云上数字创新,共建产业智慧生态
新一代云原生消息队列(一)
BigDecimal 的正确使用方式
2022/0524/bookstrap
Flir Blackfly S 工业相机:配置多个摄像头进行同步拍摄
ROS learning (21) robot slam function package -- installation and testing of orbslam
Integrated navigation: product description and interface description of zhonghaida inav2
6 seconds to understand the book to the Kindle
Recommended collection!! Which is the best flutter status management plug-in? Please look at the ranking list of yard farmers on the island!
Cat recycling bin
Centros 8 installation MySQL Error: The gpg Keys listed for the "MySQL 8.0 Community Server" repository are already ins
Command injection of cisp-pte
猫猫回收站
建议收藏!!Flutter状态管理插件哪家强?请看岛上码农的排行榜!
Tips for web development: skillfully use ThreadLocal to avoid layer by layer value transmission
Treadpoolconfig thread pool configuration in real projects
猿桌派第三季开播在即,打开出海浪潮下的开发者新视野
Sensor: introduction of soil moisture sensor (xh-m214) and STM32 drive code
解密函数计算异步任务能力之「任务的状态及生命周期管理」