当前位置:网站首页>点云配准--gicp原理与其在pcl中的使用
点云配准--gicp原理与其在pcl中的使用
2022-06-12 12:10:00 【xinxiangwangzhi_】
总结:gicp引入了概率信息(使用协方差阵),提出了icp的统一模型,既可以解释点到点和点到面的icp,也在新模型理论的基础上,提出了一种面到面的icp。
论文原文:《Generalized-ICP》
gicp统一模型(Generalized-ICP)
在概率模型中假设存在配准中两个点集, A ^ = { a i ^ } \hat{A}=\left\{\hat{a_{i}}\right\} A^={ ai^} and B ^ = { b i ^ } \hat{B}=\left\{\hat{b_{i}}\right\} B^={ bi^},并且假设 A A A and B B B 分别服从 a i ∼ N ( a i ^ , C i A ) a_{i} \sim \mathcal{N}\left(\hat{a_{i}}, C_{i}^{A}\right) ai∼N(ai^,CiA)and b i ∼ N ( b ^ i , C i B ) b_{i} \sim \mathcal{N}\left(\hat{b}_{i}, C_{i}^{B}\right) bi∼N(b^i,CiB)正态分布. { C i A } \left\{C_{i}^{A}\right\} { CiA} and { C i B } \left\{C_{i}^{B}\right\} { CiB} 分别是点对应的协方差阵. 我们假设以及匹配完成,假设变换矩阵为 T ∗ \mathbf{T}^{*} T∗, 因此:
b ^ i = T ∗ a ^ i (1) \hat{b}_{i}=\mathbf{T}^{*} \hat{a}_{i}\tag{1} b^i=T∗a^i(1)
对于变换矩阵, T \mathbf{T} T , 定义误差量 $ d_{i}^{(\mathbf{T})}= b_{i}-\mathbf{T} a_{i} $, 因为假设 $ a_{i} $ and $ b_{i} $ 服从正态分布(NDT也是假设服从正态分布), 因此 d i ( T ∗ ) d_{i}^{\left(\mathrm{T}^{*}\right)} di(T∗) 也服从正态分布:
d i ( T ∗ ) ∼ N ( b ^ i − ( T ∗ ) a ^ i , C i B + ( T ∗ ) C i A ( T ∗ ) T ) = N ( 0 , C i B + ( T ∗ ) C i A ( T ∗ ) T ) (2) \begin{aligned} d_{i}^{\left(\mathbf{T}^{*}\right)} & \sim \mathcal{N}\left(\hat{b}_{i}-\left(\mathbf{T}^{*}\right) \hat{a}_{i}, C_{i}^{B}+\left(\mathbf{T}^{*}\right) C_{i}^{A}\left(\mathbf{T}^{*}\right)^{T}\right) \\ &=\mathcal{N}\left(0, C_{i}^{B}+\left(\mathbf{T}^{*}\right) C_{i}^{A}\left(\mathbf{T}^{*}\right)^{T}\right) \end{aligned}\tag{2} di(T∗)∼N(b^i−(T∗)a^i,CiB+(T∗)CiA(T∗)T)=N(0,CiB+(T∗)CiA(T∗)T)(2)
使用最大似然估计( MLE)计算 T \mathbf{T} T :
T = argmax T ∏ i p ( d i ( T ) ) = argmax T ∑ i log ( p ( d i ( T ) ) ) (3) \mathbf{T}=\underset{\mathbf{T}}{\operatorname{argmax}} \prod_{i} p\left(d_{i}^{(\mathrm{T})}\right)=\underset{\mathbf{T}}{\operatorname{argmax}} \sum_{i} \log \left(p\left(d_{i}^{(\mathrm{T})}\right)\right)\tag{3} T=Targmaxi∏p(di(T))=Targmaxi∑log(p(di(T)))(3)
进一步简化为:(这里从最大似然估计推导,具体过程需要研究)
T = argmin T ∑ i d i ( T ) T ( C i B + T C i A T T ) − 1 d i ( T ) (4) \mathbf{T}=\underset{\mathrm{T}}{\operatorname{argmin}} \sum_{i} d_{i}^{(\mathbf{T})^{T}}\left(C_{i}^{B}+\mathbf{T} C_{i}^{A} \mathbf{T}^{T}\right)^{-1} d_{i}^{(\mathbf{T})}\tag{4} T=Targmini∑di(T)T(CiB+TCiATT)−1di(T)(4)
当:
C i B = I C i A = 0 (5) C_{i}^{B} = I \\ C_{i}^{A} = 0\tag{5} CiB=ICiA=0(5)
就得到标准ICP:
T = argmin T ∑ i d i ( T ) T d i ( T ) = argmin T ∑ i ∥ d i ( T ) ∥ 2 (6) \begin{aligned} \mathbf{T} &=\underset{\mathbf{T}}{\operatorname{argmin}} \sum_{i} d_{i}^{(\mathrm{T})^{T}} d_{i}^{(\mathrm{T})} \\ &=\underset{\mathbf{T}}{\operatorname{argmin}} \sum_{i}\left\|d_{i}^{(\mathrm{T})}\right\|^{2} \end{aligned}\tag{6} T=Targmini∑di(T)Tdi(T)=Targmini∑∥∥∥di(T)∥∥∥2(6)
当:
C i B = P i − 1 C i A = 0 (7) \begin{aligned} C_{i}^{B} &=\mathbf{P}_{\mathbf{i}}^{-1} \\ C_{i}^{A} &=0 \end{aligned}\tag{7} CiBCiA=Pi−1=0(7)
得到点到面的ICP:
T = argmin T { ∑ i ∥ P i ⋅ d i ∥ 2 } (8) \mathbf{T}=\underset{\mathbf{T}}{\operatorname{argmin}}\left\{\sum_{i}\left\|\mathbf{P}_{\mathbf{i}} \cdot d_{i}\right\|^{2}\right\}\tag{8} T=Targmin{ i∑∥Pi⋅di∥2}(8)
plane to plane ICP(gicp:相对于点到点和点到面加入概率模型(协方差阵))
点到平面算法的做法是,假设点云具有平面特征,这意味着在3D空间处理采样2D流形。
由于现实世界的曲面至少是分段可微的,我们可以假设我们的数据集是局部平面的。此外,由于我们从两个不同的角度对流形进行采样,因此通常不会对完全相同的点进行采样(即,对应关系永远不会是精确的)。
本质上,每个测量点仅提供沿其曲面法线的约束。为了对这种结构进行建模,我们考虑每个采样点沿其局部平面以高协方差分布,而在曲面法线方向(垂直于平面方向)以极低协方差分布(即点云分布在局部平面上)。假设局部拟合平面上某一点的法向量e1是沿X轴的,链接1,则该点协方差矩阵变为:
( ϵ 0 0 0 1 0 0 0 1 ) (9) \left(\begin{array}{lll} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)\tag{9} ⎝⎛ϵ00010001⎠⎞(9)
ϵ \epsilon ϵ是沿着法线方向极小的常数。
因为实际上法向量并不一定是沿x轴方向,所以需要进行坐标转换。假设 b i , a i b_i,a_i bi,ai对应的法向量分别为 u i , v i u_i,v_i ui,vi,则它们对应的协方差阵为:
C i B = R μ i ⋅ ( ϵ 0 0 0 1 0 0 0 1 ) ⋅ R μ i T C i A = R ν i ⋅ ( ϵ 0 0 0 1 0 0 0 1 ) ⋅ R ν i T \begin{array}{l} C_{i}^{B}=\mathbf{R}_{\mu_{i}} \cdot\left(\begin{array}{ccc} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \cdot \mathbf{R}_{\mu_{i}}^{T} \\ C_{i}^{A}=\mathbf{R}_{\nu_{i}} \cdot\left(\begin{array}{ccc} \epsilon & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) \cdot \mathbf{R}_{\nu_{i}}^{T} \end{array} CiB=Rμi⋅⎝⎛ϵ00010001⎠⎞⋅RμiTCiA=Rνi⋅⎝⎛ϵ00010001⎠⎞⋅RνiT
R ν i \mathbf{R}_{\nu_{i}} Rνi为e1到vi旋转矩阵。
上述协方差计算过程可以表述如下图,链接2:
确定协方差阵后利用公式(4)即为plane to plane ICP或者叫GICP。
这里其实就是怎么确定协方差阵。
显然可以通过pca计算协方差阵(代替上述求解过程):
C = 1 N ⋅ ∑ i = 1 N ⋅ ( p i − p ˉ ) ⋅ ( p i − p ˉ ) T C=\frac{1}{N} \cdot \sum_{i=1}^{N} \cdot\left(p_{i}-\bar{p}\right) \cdot\left(p_{i}-\bar{p}\right)^{T} C=N1⋅i=1∑N⋅(pi−pˉ)⋅(pi−pˉ)T
pca求解时要注意公式(4)对协方差有个求逆过程,需要注意当协方差阵奇异时,用微小量替代0值(类似NDT中处理方式)。
PCL中GICP代码应用
#include <pcl/point_types.h>
#include <pcl/point_cloud.h>
#include <pcl/registration/gicp.h>
int gicp(const pcl::PointCloud<pcl::PointXYZ>::Ptr src_cloud,
const pcl::PointCloud<pcl::PointXYZ>::Ptr tgt_cloud,
pcl::PointCloud<pcl::PointXYZ>::Ptr transformed_source)
{
pcl::GeneralizedIterativeClosestPoint<pcl::PointXYZ, pcl::PointXYZ> gicp;
gicp.setInputSource(src_cloud);
gicp.setInputTarget(tgt_cloud);
//gicp.setMaximumIterations(max_iter);
gicp.align(*transformed_source);
return 1;
}
边栏推荐
- LeetCode 890. Find and replace mode (analog + double hash table)
- [foundation of deep learning] learning of neural network (4)
- Compiling Draco library on Windows platform
- Win7 registers out of process components, services, and COM component debugging
- MySQL review
- JS将DOM导出为图片的方法
- Load/store instruction addressing mode of arm instruction set (2)
- [foundation of deep learning] back propagation method (1)
- Longest string without duplicate characters (leetcode 3)
- Traditional DOM rendering?
猜你喜欢

Dom+js+ carousel map + no time

Visio 2019 uses PJ

无重复字符的最长字符串(LeetCode 3)

mysql复习

必杀技--使用FFmpeg命令快速精准剪切视频
promise的理解已经利用promise实现图片的预加载(顺序加载)

Promise understanding has used promise to realize picture preloading (sequential loading)
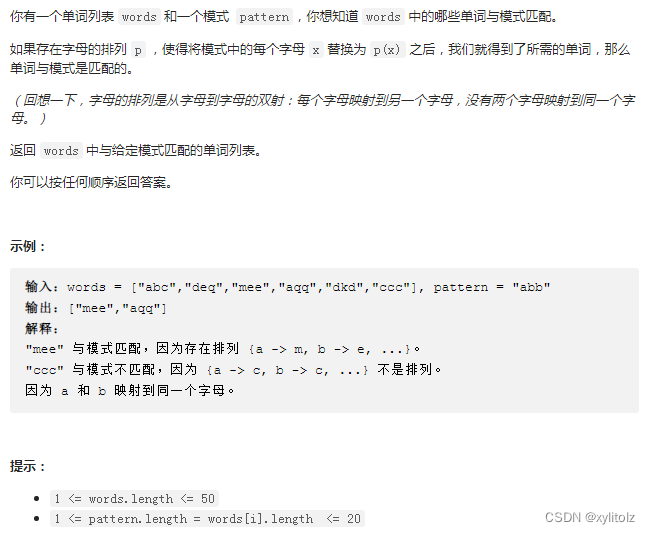
LeetCode 890. Find and replace mode (analog + double hash table)

The second day of QML study

Batch load/store instructions of arm instruction set
随机推荐
TinyMCE series (II) TinyMCE plug-in development
Find the median of two ordered arrays (leetcode 4)
stress - 系统压力模拟工具
导航中,添加边框影响布局的解决方法
B. Wall painting (C language)
Load/store access instruction of arm instruction set (2)
Rich text editor copying pictures in word documents
你不会只会用console.log()吧?
The second day of QML study
QML学习 第二天
【Leetcode】416. Split equal sum subset
传统的DOM渲染方式?
LeetCode 497. Random points in non overlapping rectangles (prefix and + bisection)
【Leetcode】221. Largest Square
树的前序,中序,后序遍历
What is modularity? Benefits of modularity
开源项目-(ERP+酒店+电商)后台管理系统
Stress - system pressure simulation tool
异步路径处理
Decision tree of machine learning