当前位置:网站首页>Natural language processing series (III) -- LSTM
Natural language processing series (III) -- LSTM
2022-07-02 11:56:00 【raelum】
notes : This article is about Summative article , Not for beginners
Catalog
One 、 Structure comparison
Only single hidden layer and one-way RNN, Ignore output layer , First of all to see Vanilla RNN In a cell Structure :
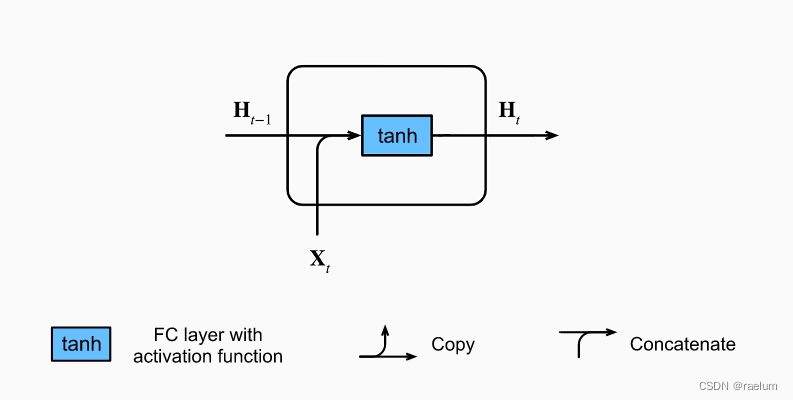
The calculation process is as follows ( Set the batch size to N N N, The number of hidden layer nodes is h h h, The number of input features is d d d):
H t = tanh ( X t W x h + H t − 1 W h h + b h ) {\bf H}_t=\tanh({\bf X}_t{\bf W}_{xh}+{\bf H}_{t-1}{\bf W}_{hh}+{\boldsymbol b}_h) Ht=tanh(XtWxh+Ht−1Whh+bh)
The shape of each parameter is :
- H t , H t − 1 {\bf H}_t,{\bf H}_{t-1} Ht,Ht−1: N × h N\times h N×h;
- X t {\bf X}_t Xt: N × d N\times d N×d;
- W x h {\bf W}_{xh} Wxh: d × h d\times h d×h;
- W h h {\bf W}_{hh} Whh: h × h h\times h h×h;
- b h {\boldsymbol b}_{h} bh: 1 × h 1\times h 1×h.
At the time of calculation , b h {\boldsymbol b}_{h} bh The broadcast mechanism will be copied from top to bottom into N × h N\times h N×h The shape of the .
LSTM In a cell Structure :
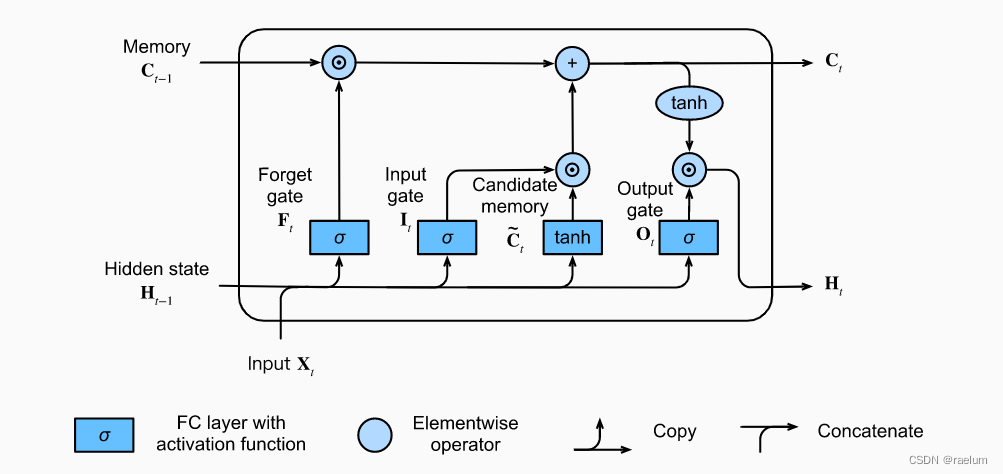
The calculation process is as follows ( set up σ ( ⋅ ) \sigma(\cdot) σ(⋅) representative Sigmoid ( ⋅ ) \text{Sigmoid}(\cdot) Sigmoid(⋅)):
I t = σ ( X t W x i + H t − 1 W h i + b i ) F t = σ ( X t W x f + H t − 1 W h f + b f ) O t = σ ( X t W x o + H t − 1 W h o + b o ) C ~ t = tanh ( X t W x c + H t − 1 W h c + b c ) C t = F t ⊙ C t − 1 + I t ⊙ C ~ t H t = O t ⊙ tanh ( C t ) \begin{aligned} {\bf I}_t&=\sigma({\bf X}_t{\bf W}_{xi}+{\bf H}_{t-1}{\bf W}_{hi}+{\boldsymbol b}_i) \\ {\bf F}_t&=\sigma({\bf X}_t{\bf W}_{xf}+{\bf H}_{t-1}{\bf W}_{hf}+{\boldsymbol b}_f) \\ {\bf O}_t&=\sigma({\bf X}_t{\bf W}_{xo}+{\bf H}_{t-1}{\bf W}_{ho}+{\boldsymbol b}_o) \\ \tilde{ {\bf C}}_t&=\tanh({\bf X}_t{\bf W}_{xc}+{\bf H}_{t-1}{\bf W}_{hc}+{\boldsymbol b}_c) \\ {\bf C}_t&={\bf F}_t \odot{\bf C}_{t-1}+{\bf I}_t\odot \tilde{ {\bf C}}_t \\ {\bf H}_t&={\bf O}_t\odot \tanh({\bf C}_t) \\ \end{aligned} ItFtOtC~tCtHt=σ(XtWxi+Ht−1Whi+bi)=σ(XtWxf+Ht−1Whf+bf)=σ(XtWxo+Ht−1Who+bo)=tanh(XtWxc+Ht−1Whc+bc)=Ft⊙Ct−1+It⊙C~t=Ot⊙tanh(Ct)
among ⊙ \odot ⊙ It's matrix Hadamard product , The shape of each parameter is as follows :
- H t , H t − 1 {\bf H}_t,{\bf H}_{t-1} Ht,Ht−1、 I t , F t , O t {\bf I}_t,{\bf F}_t,{\bf O}_t It,Ft,Ot、 C ~ t , C t , C t − 1 \tilde{ {\bf C}}_t,{\bf C}_t,{\bf C}_{t-1} C~t,Ct,Ct−1: N × h N\times h N×h;
- X t {\bf X}_t Xt: N × d N\times d N×d;
- W x i , W x f , W x o , W x c {\bf W}_{xi},{\bf W}_{xf},{\bf W}_{xo},{\bf W}_{xc} Wxi,Wxf,Wxo,Wxc: d × h d\times h d×h;
- W h i , W h f , W h o , W h c {\bf W}_{hi},{\bf W}_{hf},{\bf W}_{ho},{\bf W}_{hc} Whi,Whf,Who,Whc: h × h h\times h h×h;
- b i , b f , b o , b c {\boldsymbol b}_{i},{\boldsymbol b}_{f},{\boldsymbol b}_{o},{\boldsymbol b}_{c} bi,bf,bo,bc: 1 × h 1\times h 1×h
Two 、LSTM Basics
LSTM There are three doors : I t , F t , O t {\bf I}_t,{\bf F}_t,{\bf O}_t It,Ft,Ot Each represents the input gate 、 Forgetting gate and output gate . The input gate is used to control how much is used from C ~ t \tilde{ {\bf C}}_t C~t New data for , Forgetting gate is used to control how much is reserved C t − 1 {\bf C}_{t-1} Ct−1 The content of , The output gate is used to control how much memory information is transferred to the next time step .
about LSTM, Only consider batch_first=True The circumstances of , The shape of the input data is L × N × d L\times N\times d L×N×d. In addition, you need to enter H 0 {\bf H}_0 H0 and C 0 {\bf C}_0 C0, Its shape is 1 × N × h 1\times N\times h 1×N×h.
LSTM The output on all time steps is [ H 1 , H 2 , ⋯ , H L ] L × N × h [{\bf H}_1,{\bf H}_2,\cdots,{\bf H}_L]_{L\times N\times h} [H1,H2,⋯,HL]L×N×h and [ C 1 , C 2 , ⋯ , C L ] L × N × h [{\bf C}_1,{\bf C}_2,\cdots,{\bf C}_L]_{L\times N\times h} [C1,C2,⋯,CL]L×N×h. among H t {\bf H}_t Ht representative t t t The hidden state of time , C t {\bf C}_t Ct representative t t t The memory of the moment .
3、 ... and 、 Build from scratch LSTM
Do not consider the parameters between the hidden layer and the output layer , It can be seen that LSTM There are a total of parameters to learn 4 4 4 Group , namely : ( W x ∗ , W h ∗ , b ∗ ) , where ∗ = i , f , o , c ({\bf W}_{x*},{\bf W}_{h*},{\boldsymbol b}_{*}),\; \text{where}\;*=i,f,o,c (Wx∗,Wh∗,b∗),where∗=i,f,o,c. Therefore, we can initialize the corresponding parameters by groups .
LSTM There are a total of parameters to learn 3 × 4 = 12 3\times4=12 3×4=12 individual , comparison Vanilla RNN Of 3 3 3 There are many more parameters .
First, import all packages involved in the code in this article :
import math
import string
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
We define a function to initialize a set of parameters . Notice that the shape of each set of parameters is ( d × h , h × h , 1 × h ) (d\times h,h\times h,1\times h) (d×h,h×h,1×h):
def init_group_params(input_size, hidden_size):
std = math.sqrt(2 / (input_size + hidden_size))
return nn.Parameter(torch.randn(input_size, hidden_size) * std), \
nn.Parameter(torch.randn(hidden_size, hidden_size) * std), \
nn.Parameter(torch.randn(1, hidden_size) * std)
Next build LSTM( imitation nn.LSTM, That is, the parameters between the hidden layer and the output layer are not included ):
class LSTM(nn.Module):
def __init__(self, input_size, hidden_size):
super().__init__()
self.W_xi, self.W_hi, self.b_i = init_group_params(input_size, hidden_size)
self.W_xf, self.W_hf, self.b_o = init_group_params(input_size, hidden_size)
self.W_xo, self.W_ho, self.b_f = init_group_params(input_size, hidden_size)
self.W_xc, self.W_hc, self.b_c = init_group_params(input_size, hidden_size)
def forward(self, inputs, h_0, c_0):
L, N, d = inputs.shape
H, C = h_0[0], c_0[0]
outputs = []
for t in range(L):
X = inputs[t]
I = torch.sigmoid(X @ self.W_xi + H @ self.W_hi + self.b_i)
F = torch.sigmoid(X @ self.W_xf + H @ self.W_hf + self.b_f)
O = torch.sigmoid(X @ self.W_xo + H @ self.W_ho + self.b_o)
C_temp = torch.tanh(X @ self.W_xc + H @ self.W_hc + self.b_c)
C = F * C + I * C_temp
H = O * torch.tanh(C)
outputs.append(H)
h_n, c_n = H.unsqueeze(0), C.unsqueeze(0)
outputs = torch.cat(outputs, 0).unsqueeze(1)
return outputs, h_n, c_n
Finally, build the model , At this time, we need to add a linear layer ( Output layer ):
class Model(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super().__init__()
self.lstm = LSTM(input_size, hidden_size)
self.linear = nn.Linear(hidden_size, output_size)
def forward(self, x):
# All zero initialization h_0 and c_0
_, h_n, _ = self.lstm(x, torch.zeros(1, x.shape[1], self.linear.in_features).to(device),
torch.zeros(1, x.shape[1], self.linear.in_features).to(device))
return self.linear(h_n[0])
Four 、 Test our LSTM
To verify the built LSTM Is the right model , We need it to complete a task .
4.1 Character prediction task
Generally speaking , That is, given a word ( The length is n n n), When the model is read n − 1 n-1 n−1 After two letters , It can accurately predict the last letter . for example , For words machine, When the model is read machin after , It should give a prediction :e.
It should be noted that , Character prediction tasks are not perfect . For example, given the first two letters
be, The third letter is eitherestilltCan form a word , And the test set is limited , There may be only one answer .
We use word data sets ( Download address ), The training set contains 8000 Word , The test set contains 2000 Word , And the training set and the test set do not coincide .
4.2 Data preprocessing
LSTM Cannot recognize letters directly , Therefore, we need to convert a single letter into a tensor (one-hot code ):
def letter2tensor(letter):
letter_idx = torch.tensor(string.ascii_lowercase.index(letter))
return F.one_hot(letter_idx, num_classes=len(string.ascii_lowercase))
Then create a function to convert the whole word into the corresponding tensor ( Here we regard a word as a batch, So the shape is L × 1 × d L\times1\times d L×1×d, among d = 26 d=26 d=26, L L L Is the length of the word ):
def word2tensor(word):
result = torch.zeros(len(word), len(string.ascii_lowercase))
for i in range(len(word)):
result[i] = letter2tensor(word[i])
return result.unsqueeze(1)
for example :
print(word2tensor('cat'))
# tensor([[[0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
# [[1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 0., 0., 0., 0., 0., 0., 0.]],
# [[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0., 1., 0., 0., 0., 0., 0., 0.]]])
Read training set and test set :
with open('words/train.txt') as f:
train_data = f.read().strip().split('\n')
with open('words/test.txt') as f:
test_data = f.read().strip().split('\n')
print(train_data[0], test_data[1])
# clothe trend
Besides , In order to ensure the reproducibility of the results , We also need to set seeds :
def setup_seed(seed):
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
4.3 Training and testing
We will train on the training set 5 individual epoch, because batch_size=1, So every 800 individual Iteration Output a loss and calculate the accuracy of the model on the test set at this time , Finally, draw the corresponding curve .
setup_seed(42)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# In effect 26 Classification task , So the number of neurons in the output layer is 26
model = Model(26, 64, 26)
model.to(device)
LR = 7e-3 # Learning rate
EPOCHS = 5 # How many? epoch
INTERVAL = 800 # How many? iteration Output a
critertion = nn.CrossEntropyLoss()
# use SGD The optimizer will have the same precision of the test set
optimizer = torch.optim.Adam(model.parameters(), lr=LR, weight_decay=3e-4)
train_loss = []
test_acc = []
avg_train_loss = 0 # Average loss of training set
correct = 0 # The model predicts the correct number on the test set
for epoch in range(EPOCHS):
print(f'Epoch {
epoch+1}')
print('-' * 62)
for iteration in range(len(train_data)):
full_word = train_data[iteration]
# Reading is the front n-1 Letters , The last letter is used as target
X = word2tensor(full_word[:-1]).to(device)
target = torch.tensor([string.ascii_lowercase.index(full_word[-1])]).to(device)
# Positive communication
output = model(X)
loss = critertion(output, target)
avg_train_loss += loss
# Back propagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# every other 800 individual iteration Output a loss and calculate the accuracy of the model on the test set
if (iteration + 1) % INTERVAL == 0:
avg_train_loss /= INTERVAL
train_loss.append(avg_train_loss.item())
# Calculate the prediction accuracy of the model on the test set
with torch.no_grad():
for test_word in test_data:
X = word2tensor(test_word[:-1]).to(device)
target = torch.tensor(string.ascii_lowercase.index(test_word[-1])).to(device)
pred = model(X)
correct += (pred.argmax() == target).sum().item()
acc = correct / len(test_data)
test_acc.append(acc)
print(
f'Iteration: [{
iteration + 1:04}/{
len(train_data)}] | Train Loss: {
avg_train_loss:.4f} | Test Acc: {
acc:.4f}'
)
avg_train_loss, correct = 0, 0
print()
Only the last one is shown here epoch Output :
Epoch 5
--------------------------------------------------------------
Iteration: [0800/8000] | Train Loss: 1.2918 | Test Acc: 0.6000
Iteration: [1600/8000] | Train Loss: 1.1903 | Test Acc: 0.5910
Iteration: [2400/8000] | Train Loss: 1.2615 | Test Acc: 0.6075
Iteration: [3200/8000] | Train Loss: 1.2236 | Test Acc: 0.6015
Iteration: [4000/8000] | Train Loss: 1.2355 | Test Acc: 0.5925
Iteration: [4800/8000] | Train Loss: 1.1314 | Test Acc: 0.6050
Iteration: [5600/8000] | Train Loss: 1.2172 | Test Acc: 0.6045
Iteration: [6400/8000] | Train Loss: 1.1808 | Test Acc: 0.6140
Iteration: [7200/8000] | Train Loss: 1.2092 | Test Acc: 0.6185
Iteration: [8000/8000] | Train Loss: 1.1845 | Test Acc: 0.6040
draw a curve :
step = INTERVAL / len(train_data)
plt.plot(np.arange(step, EPOCHS + step, step), train_loss, label="train loss")
plt.plot(np.arange(step, EPOCHS + step, step), test_acc, label="test acc")
plt.legend(loc="best", fontsize=12)
plt.xlabel('epoch')
plt.show()
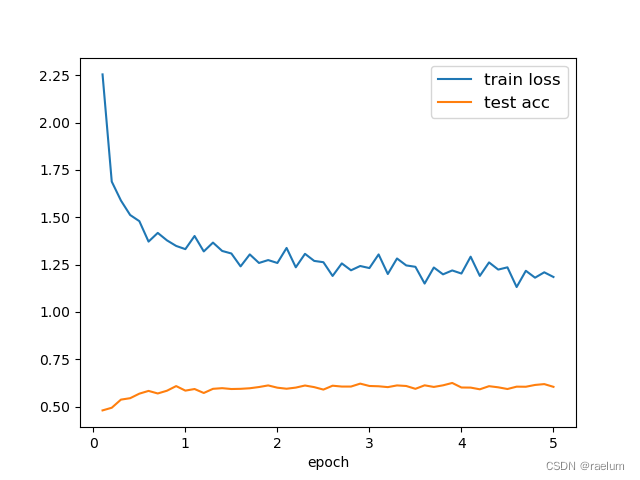
As can be seen from the above figure , The prediction accuracy of the model on the test set tends to 0.6 0.6 0.6, The reasons may be as follows :
- The quality of the dataset is poor ;
- Data sets are too simple ,LSTM There's over fitting ;
- Our task is not enough “ Self consistent ”.
边栏推荐
- Seriation in R: How to Optimally Order Objects in a Data Matrice
- Homer forecast motif
- 基于Hardhat和Openzeppelin开发可升级合约(一)
- 预言机链上链下调研
- TDSQL|就业难?腾讯云数据库微认证来帮你
- 【多线程】主线程等待子线程执行完毕在执行并获取执行结果的方式记录(有注解代码无坑)
- MySQL linked list data storage query sorting problem
- Implementation of address book (file version)
- Pyqt5+opencv project practice: microcirculator pictures, video recording and manual comparison software (with source code)
- php 二维、多维 数组打乱顺序,PHP_php打乱数组二维数组多维数组的简单实例,php中的shuffle函数只能打乱一维
猜你喜欢

Thesis translation: 2022_ PACDNN: A phase-aware composite deep neural network for speech enhancement
YYGH-BUG-04

From scratch, develop a web office suite (3): mouse events
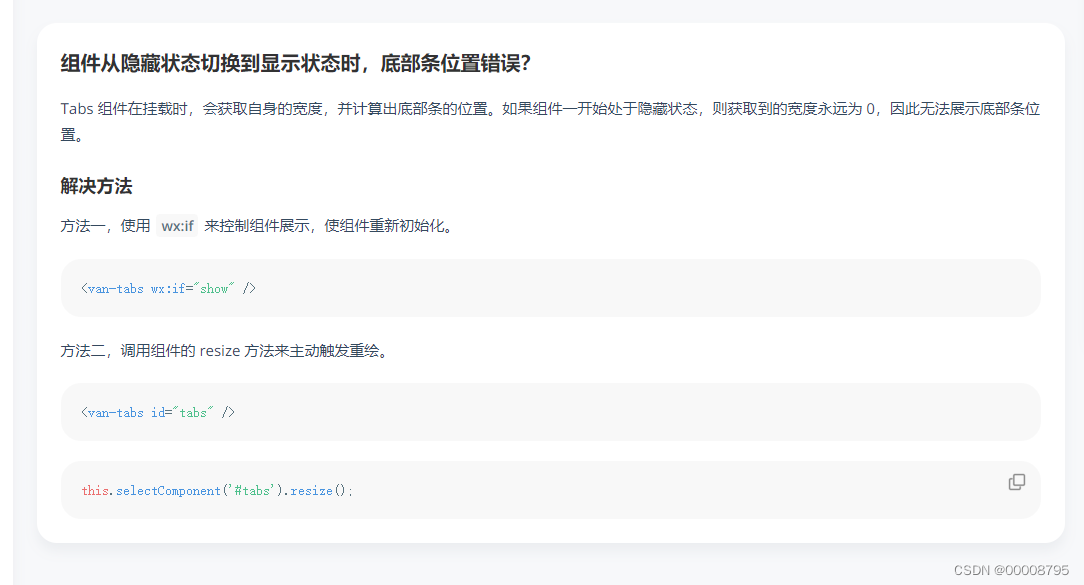
vant tabs组件选中第一个下划线位置异常

RPA advanced (II) uipath application practice

What is the relationship between digital transformation of manufacturing industry and lean production

HOW TO ADD P-VALUES ONTO A GROUPED GGPLOT USING THE GGPUBR R PACKAGE

念念不忘,必有回响 | 悬镜诚邀您参与OpenSCA用户有奖调研
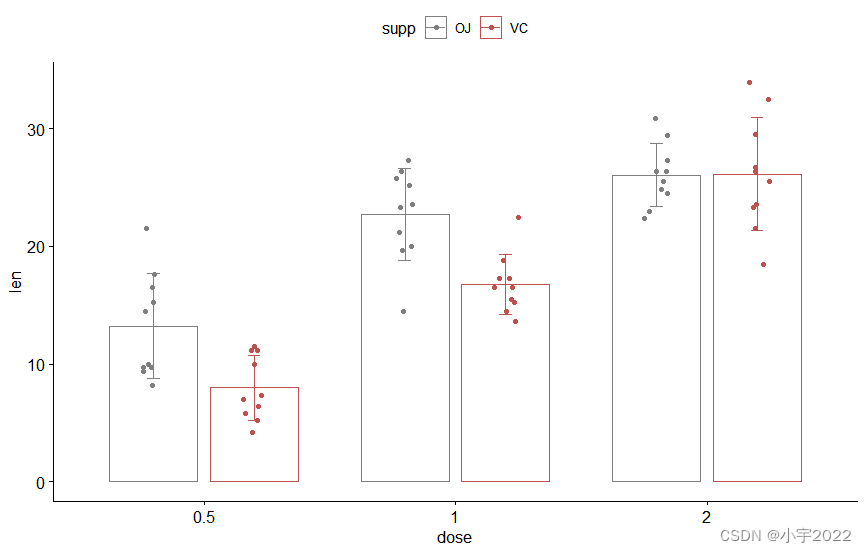
HOW TO EASILY CREATE BARPLOTS WITH ERROR BARS IN R

文件操作(详解!)
随机推荐
Flesh-dect (media 2021) -- a viewpoint of material decomposition
QT获取某个日期是第几周
Amazon cloud technology community builder application window opens
PHP query distance according to longitude and latitude
HOW TO ADD P-VALUES TO GGPLOT FACETS
Data analysis - Matplotlib sample code
HOW TO CREATE AN INTERACTIVE CORRELATION MATRIX HEATMAP IN R
揭露数据不一致的利器 —— 实时核对系统
Fabric. JS 3 APIs to set canvas width and height
2022年遭“挤爆”的三款透明LED显示屏
Dynamic debugging of multi file program x32dbg
机械臂速成小指南(七):机械臂位姿的描述方法
Wechat applet uses Baidu API to achieve plant recognition
easyExcel和lombok注解以及swagger常用注解
Seriation in R: How to Optimally Order Objects in a Data Matrice
Precautions for scalable contract solution based on openzeppelin
抖音海外版TikTok:正与拜登政府敲定最终数据安全协议
to_ Bytes and from_ Bytes simple example
Power Spectral Density Estimates Using FFT---MATLAB
Liftover for genome coordinate conversion