第五章-5.2-指示器随机变量

一、关于指示器随机变量

1、给定一个样本空间S和一个事件A，事件A对应的指示器随机变量为

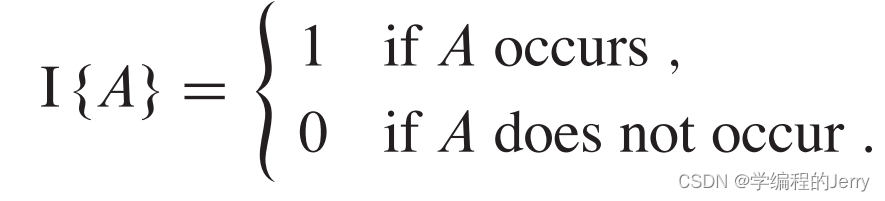
2、举个例子：

样本空间为S={H、T}，其中Pr{H}和Pr{T}概率均为1/2，下面定义一个指示器随机变量XH,对应硬币正面朝上的事件H,正面朝上对应1，反面对应0，那么可算出期望值：

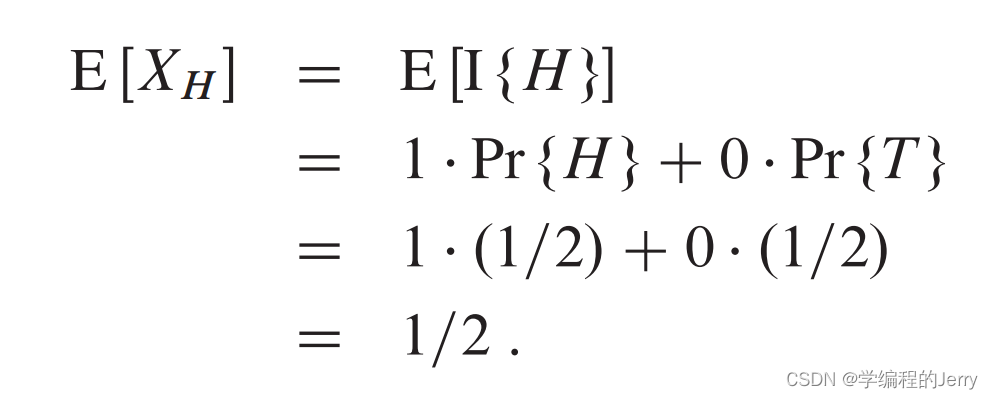
 由图中可以观察到，一个事件A对应的指示器随机变量的期望值等于事件A发生的概率。

二、引理5.1

1、内容：给定一个样本空间S和S中的一个事件A，设XA=I{A}，那么

2、证明：

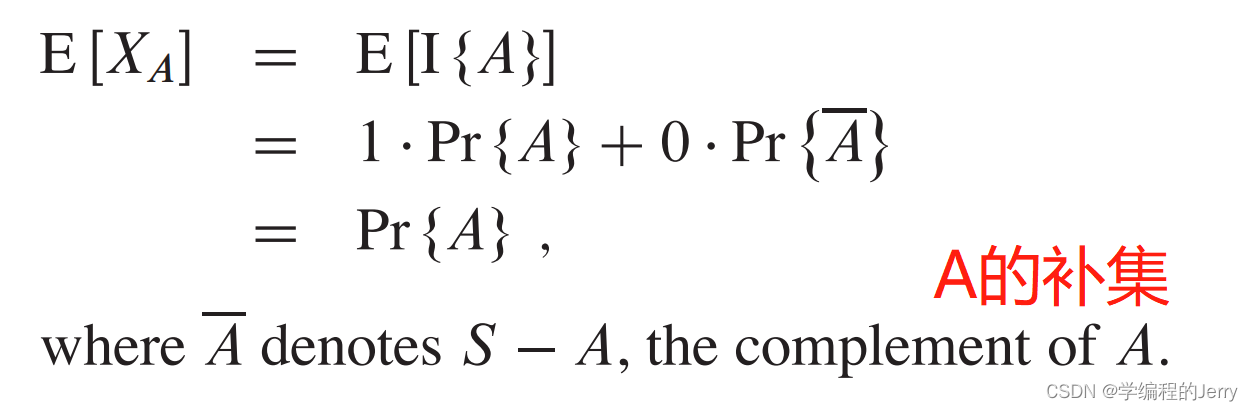
3、举个例子:

设指示器随机变量Xi对应第i次抛硬币正面朝上的事件：Xi = {第i次抛硬币出现事件H，正面朝上值为1，反之则为0}，设随机变量X表示n次抛硬币出现正面的总次数，从而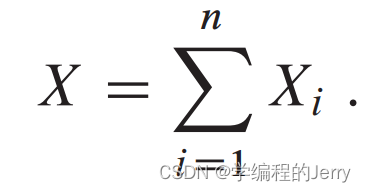

 两边均取期望值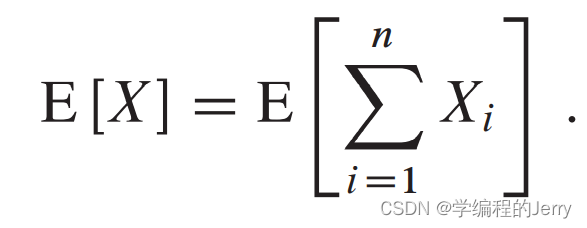：，然后可得

 ​​​​​​​​​​​​​​

 

三、用指示器随机变量分析雇用问题

Step1:定义变量

我们定义n个变量，与每个应聘者是否被雇用对应。

 Step2:观察伪代码

HIRE-ASSISTANT(n)
//candidate 0 is a least-qualified dummy candidate（第一个雇佣者编号为0，比其他雇佣者更差）
1 best = 0
2 for i = 1 to n
3     interview candidate i
4     if candidate i is better than candidate best
5         best = i
6         hire candidate i

Step3:计算概率

我们必须计算第5、6行被执行的概率。假设应聘者以随机顺序出现，那么前i个中每一个人都有1/i的概率是这i个人中最优秀的，那么它们都有1/i的概率受到雇用。由引理5.1可得：

Step4:计算E[X]

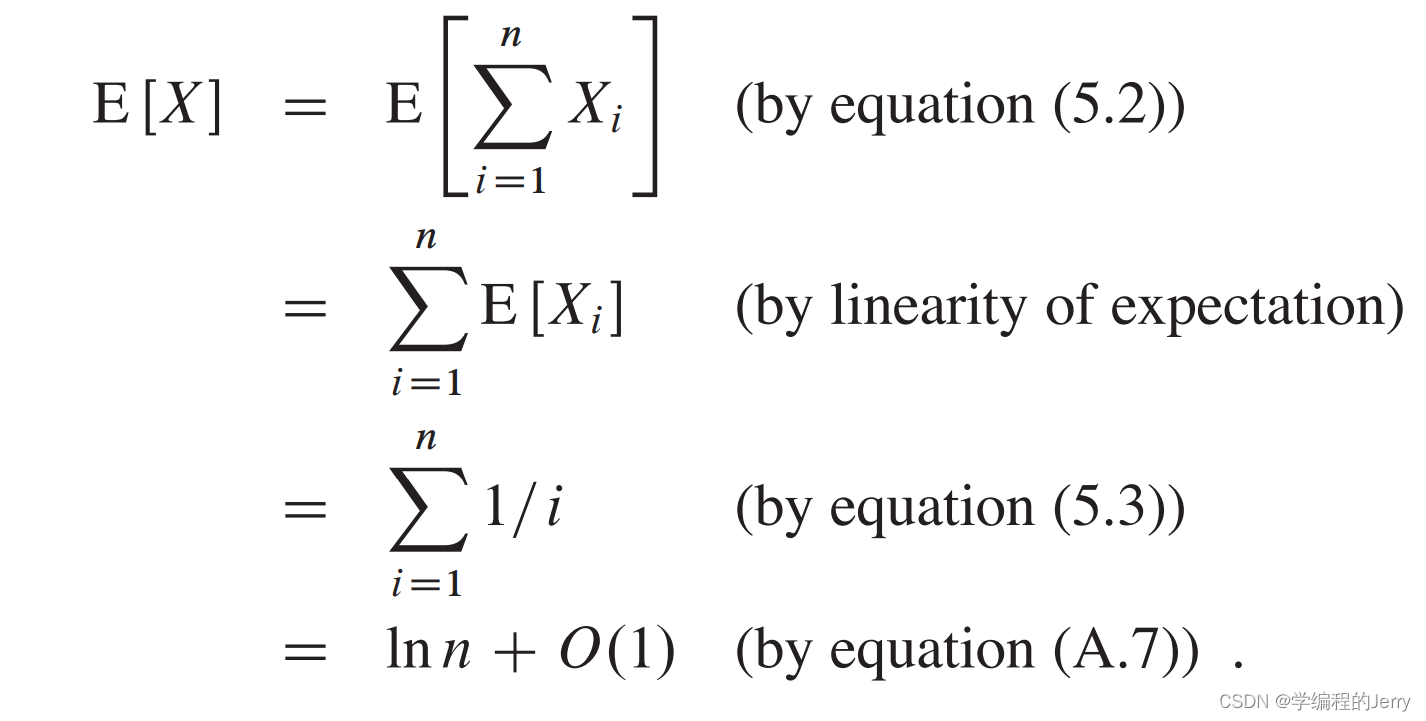
 Step5:总结

尽管我们面试了n个人，但是平均起来大概只雇用了他们当中ln n个人。

三、引理5.2

1、内容：假设应聘者以随机次序出现，算法HIRE-ASSISTANT总的雇用费用大约是​​​​​​​

 2、证明：

上面的式子可以直接推出，可见这比最坏情况O(ch*n)要好很多。