当前位置:网站首页>54. Spiral matrix & 59 Spiral matrix II ●●
54. Spiral matrix & 59 Spiral matrix II ●●
2022-07-05 04:50:00 【chenyfan_】
54. Spiral matrix ●●
To give you one m That's ok n Columns of the matrix matrix , Please follow Clockwise spiral sequence , Returns all elements in the matrix .
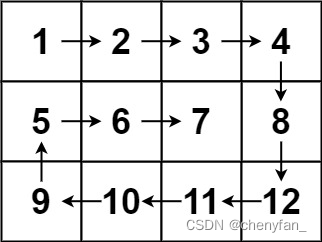
Input :matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output :[1,2,3,4,8,12,11,10,9,5,6,7]
- simulation
The four edges traverse in order , Move 、 Judgement boundary .
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
int m = matrix.size(); // m That's ok
int n = matrix[0].size(); // n Column
int top = 0, right = n-1, left = 0, buttom = m-1; // Boundary index value
int numsize = m*n;
int num = 0;
vector<int> ans(numsize);
while(true){
for(int i = left; i <= right; i++){
ans[num++] = matrix[top][i];
}
top++;
if(top>buttom) break; // Traverse Judgement boundary
for(int i = top; i <= buttom; i++){
ans[num++] = matrix[i][right];
}
right--;
if(left>right) break;
for(int i = right; i >= left; i--){
ans[num++] = matrix[buttom][i];
}
buttom--;
if(top>buttom) break;
for(int i = buttom; i >= top; i--){
ans[num++] = matrix[i][left];
}
left++;
if(left>right) break;
}
return ans;
}
};
59. Spiral matrix II ●●
Give you a positive integer n , Generate a include 1 To n 2 n^2 n2 All the elements , And the element press Clockwise order Spirally arranged n x n square matrix matrix .
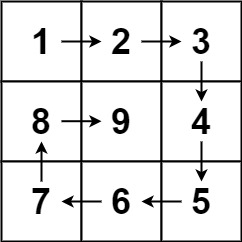
Input :n = 3
Output :[[1,2,3],[8,9,4],[7,6,5]]
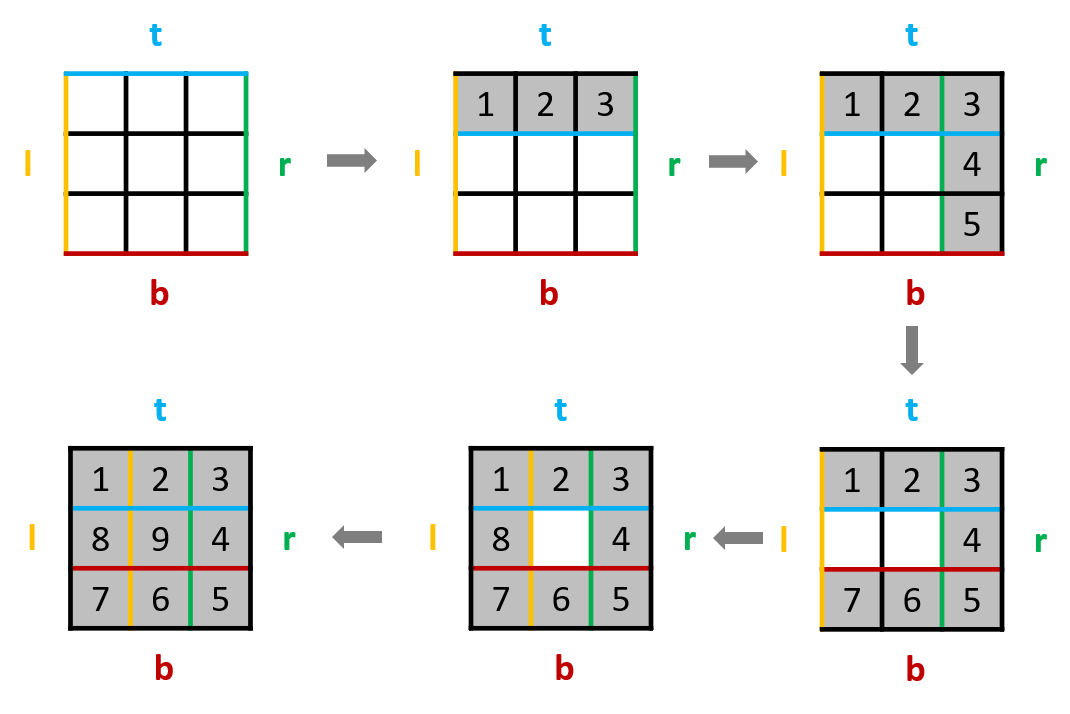
- Generate a n×n Empty matrix ans, Then simulate the whole inward surrounding filling process :
- Define the current left and right upper and lower boundaries l,r,t,b, Initial value num = 1, Iteration termination value numsize = n * n;
- When num <= numsize when , Always follow From left to right From top to bottom From right to left From bottom to top Fill in the sequence loop , After each filling :
- perform num += 1: Get the next number to fill in ;
- Update boundaries : For example, after filling in from left to right , Upper boundary t += 1, Equivalent to the upper boundary shrinking inward 1.
- Use num <= numsize instead of l < r || t < b As an iterative condition , In order to Solve when n In an odd number of , The problem that the central number of the matrix cannot be filled in during the iteration .
- Eventually return ans that will do .
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> ans(n, vector<int>(n, 0));
int up = 0, down = n-1, left = 0, right = n-1;
int cnt = 1, num = n*n;
while(cnt <= num){
// Iteration conditions , Number of fillings <= Lattice number
for(int i = left; i <= right; ++i) ans[up][i] = cnt++; // Move right
++up;
for(int i = up; i <= down; ++i) ans[i][right] = cnt++; // Move down
--right;
for(int i = right; i >= left; --i) ans[down][i] = cnt++; // Move left
--down;
for(int i = down; i >= up; --i) ans[i][left] = cnt++; // Move upward
++left;
}
return ans;
}
};
边栏推荐
- History of web page requests
- Minor spanning tree
- AutoCAD - stretching
- Pdf to DWG in CAD
- Data security -- 14 -- Analysis of privacy protection governance
- Debug insights
- 【acwing】837. Number of connected block points
- On-off and on-off of quality system construction
- How can CIOs use business analysis to build business value?
- JVM 原理和流程简介
猜你喜欢
XSS injection

【Leetcode】1352. 最后 K 个数的乘积
3 minutes learn to create Google account and email detailed tutorial!

Advanced length of redis -- deletion strategy, master-slave replication, sentinel mode
![Rip notes [rip message security authentication, increase of rip interface measurement]](/img/89/f70af97676496d7b9aa867be89f11d.jpg)
Rip notes [rip message security authentication, increase of rip interface measurement]

2022-2028 global and Chinese FPGA prototype system Market Research Report
Create a pyGame window with a blue background

【acwing】240. food chain
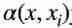
The principle of attention mechanism and its application in seq2seq (bahadanau attention)
Is $20billion a little less? Cisco is interested in Splunk?
随机推荐
Solution of circular dependency
質量體系建設之路的分分合合
The difference between bundle, chunk and module
QT Bluetooth: a class for searching Bluetooth devices -- qbluetooth devicediscoveryagent
Error statuslogger log4j2 could not find a logging implementation
Chapter 6 text processing tools for shell programming (awk)
2021 electrician Cup - high speed rail traction power supply system operation data analysis and equivalent modeling ideas + code
Neural networks and deep learning Chapter 6: Circular neural networks reading questions
Introduction to JVM principle and process
SQLServer 存储过程传递数组参数
XSS injection
Setting up redis cluster cluster under Windows
#775 Div.1 C. Tyler and Strings 组合数学
Flink cluster configuration
Flutter 小技巧之 ListView 和 PageView 的各种花式嵌套
[AI bulletin 20220211] the hard core up owner has built a lidar and detailed AI accelerator
CUDA Programming atomic operation atomicadd reports error err:msb3721, return code 1
MD5绕过
Manually implement heap sorting -838 Heap sort
2022 thinking of Mathematical Modeling B problem of American college students / analysis of 2022 American competition B problem